|
|
| Строка 22: |
Строка 22: |
| | {{Лемма | | {{Лемма |
| | |statement = Ребро <tex>(u, v)</tex> является мостом тогда и только тогда, когда <tex>(u, v)</tex> принадлежит дереву обхода в глубину и <tex>ret(v) > enter(u)</tex> | | |statement = Ребро <tex>(u, v)</tex> является мостом тогда и только тогда, когда <tex>(u, v)</tex> принадлежит дереву обхода в глубину и <tex>ret(v) > enter(u)</tex> |
| − | | proof = | + | | proof = Рассмотрим вершину <tex>v</tex> или её потомка. Из них есть обратное ребро обратное в в предка <tex>v</tex>, тогда и только тогда, когда найдется такой сын <tex>t</tex>, что <tex>ret[t] \le enter[v]</tex>. Так как, если <tex>ret[t] = enter[v]</tex>, то это означает, что найдётся обратное ребро, приходящее точно в <tex>v</tex>. Если же <tex>ret[t] < enter[v]</tex>, то это означает наличие обратного ребра в какого-либо предка вершины <tex>v</tex>. |
| − | Так как на пути от вершины к корню дерева величины <tex>enter</tex> убывают, то <tex>ret(v)</tex> возвращает величину <tex>enter</tex> для ближайшей к корню вершины, достижимой из <tex>v</tex> или ее потомка, возможно используя одно обратное ребро. Следовательно, из вершины <tex>v</tex> или ее потомков существует обратное ребро потомка <tex>u</tex> или саму <tex>u</tex> тогда и только тогда, когда <tex>ret(v) <= enter(u)</tex>. По доказанной теореме, отсутствие такого ребра эквивалентно тому что <tex>(u, v)</tex> - мост.
| + | |
| | + | Таким образом, если для текущего ребра <tex>(v, t)</tex> (принадлежащего дереву поиска) выполняется <tex>ret[t] > enter[v]</tex>, то это ребро является мостом; в противном случае оно мостом не является. |
| | }} | | }} |
| | | | |
Версия 07:06, 18 ноября 2011
Постановка задачи
Дан неориентированный граф [math] G [/math]. Найти все мосты в [math] G [/math] за время [math] O(|V| + |E|)[/math]
Алгоритм
| Теорема: |
Пусть [math] T [/math] - дерево обхода в глубину графа [math] G[/math]. Ребро [math] (u, v) [/math] является мостом тогда и только тогда, когда [math] (u, v) \in T[/math] и из вершины [math] v[/math] и любого ее потомка нет обратного ребра в вершину [math] u[/math] или предка [math] u [/math] |
| Доказательство: |
| [math]\triangleright[/math] |
|
[math] \Leftarrow[/math]
Удалим [math] (u, v)[/math] из [math] G[/math] Докажем, что мы не сможем достичь ни одного из предков [math] v [/math] (в частности [math] u [/math]). Пусть это не так, и [math] w[/math] - предпоследняя вершина на пути от [math] v[/math] до ее предка [math]x [/math]. Очевидно, [math] (w, x)[/math] не ребро дерева (в силу единственности пути в дереве). Если [math] (w, x)[/math] - обратное ребро, то это противоречит условию теоремы, т.к. [math] x[/math] - предок [math] u[/math]
[math] \Rightarrow[/math]
Пусть существует удовлетворяющее условию обратное ребро [math](x, w)[/math]. Тогда [math](u, v)[/math] лежит на цикле [math]x \rightsquigarrow v \rightarrow u \rightsquigarrow w \rightarrow x[/math] и не может быть мостом. |
| [math]\triangleleft[/math] |
Функция [math]ret(v)[/math]
Определим функцию [math]ret(v)[/math], где [math]v \in V[/math], как минимум из следущих величин
- [math]enter(v)[/math] время входа в вершину [math]v [/math]
- [math]enter(x)[/math], где [math]x[/math] - потомок [math]v[/math]
- [math]enter(x)[/math], где [math](w, x)[/math] - обратное ребро, а [math]w[/math] - потомок [math]v[/math] (в нестрогом смысле)
Лемма
| Лемма: |
Ребро [math](u, v)[/math] является мостом тогда и только тогда, когда [math](u, v)[/math] принадлежит дереву обхода в глубину и [math]ret(v) \gt enter(u)[/math] |
| Доказательство: |
| [math]\triangleright[/math] |
|
Рассмотрим вершину [math]v[/math] или её потомка. Из них есть обратное ребро обратное в в предка [math]v[/math], тогда и только тогда, когда найдется такой сын [math]t[/math], что [math]ret[t] \le enter[v][/math]. Так как, если [math]ret[t] = enter[v][/math], то это означает, что найдётся обратное ребро, приходящее точно в [math]v[/math]. Если же [math]ret[t] \lt enter[v][/math], то это означает наличие обратного ребра в какого-либо предка вершины [math]v[/math].
Таким образом, если для текущего ребра [math](v, t)[/math] (принадлежащего дереву поиска) выполняется [math]ret[t] \gt enter[v][/math], то это ребро является мостом; в противном случае оно мостом не является. |
| [math]\triangleleft[/math] |
| Утверждение: |
[math]ret(v)[/math] = [math]min([/math]
- [math]enter(v) [/math]
- [math]enter(p)[/math], [math](v, p),[/math] - обратное ребро
- [math]ret(u)[/math], [math](v, u)[/math] - ребро дерева
[math]) [/math] |
| [math]\triangleright[/math] |
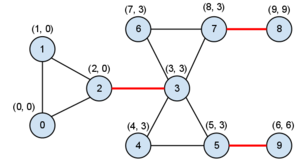 В скобах у вершины [math]u[/math] указаны [math]enter[u][/math] и [math]ret[u][/math]. Мостами будут красные красный 1)[math]enter(v) [/math]
По определению функции [math]ret[/math]
2)[math]enter(p)[/math], [math](v, p)[/math] - обратное ребро
[math]p[/math] достижима из [math]v[/math] по одному обратному ребру, значит величина [math]ret(v)[/math] не больше [math]enter(p)[/math]
3)[math]ret(u)[/math], [math]u[/math] - потомок [math]v[/math]
Так как вершина [math]u[/math] - потомок [math]v[/math], то обратное ребро из ее поддерева является обратным ребром из поддерева [math]v[/math]
|
| [math]\triangleleft[/math] |
Псевдокод
dfs([math] v [/math])
[math] time \leftarrow time + 1[/math]
[math]enter[v] \leftarrow time[/math]
[math]ret[v] \leftarrow time [/math]
for всех [math]u[/math] смежных с [math]v[/math]
if [math](v, u)[/math] - обратное ребро
[math]ret[v] \leftarrow min(ret[v], enter[u])[/math]
if вершина [math]u[/math] - белая
dfs(u)
[math] ret[v] \leftarrow min(ret[v], ret[u]) [/math]
if [math]ret[u] \gt enter[v][/math]
ребро [math](v, u)[/math] - мост
Смотри также
Источники
- Сайт e-maxx
- Свободная энциклопедия - Википедия
Литература
Седжвик Роберт. Фундаментальные алгоритмы на C++. Часть 5: Алгоритмы на графах: Пер. с англ./Роберт Седжвик. — СПб.: ООО «ДиаСофтЮП», 2002. — С. 123-128
