Коды Прюфера — различия между версиями
Berkut (обсуждение | вклад) м |
(→Коды Прюфера.) |
||
| Строка 21: | Строка 21: | ||
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | По любой последовательности | + | По любой последовательности длины <tex>n - 2</tex> из чисел от <tex>1</tex> до <tex>n</tex> можно построить помеченное дерево, |
для которого эта последовательность является кодом Прюфера. | для которого эта последовательность является кодом Прюфера. | ||
|proof= | |proof= | ||
| − | Доказательство проведем по индукции. | + | Доказательство проведем по индукции. <br> |
База. <tex>n = 1</tex> <tex>-</tex> верно. | База. <tex>n = 1</tex> <tex>-</tex> верно. | ||
<br> | <br> | ||
Версия 09:41, 11 декабря 2011
Содержание
Коды Прюфера.
Кодирование Прюфера переводит помеченные деревья порядка в последовательность чисел от до по алгоритму:
Пока количество вершин больше одной {
1. Выбирается лист с минимальным номером.
2. В код Прюфера добавляется номер вершины, смежной с .
3. Вершина и инцидентное ей ребро удаляются из дерева.
}
Полученная последовательность называется кодом Прюфера для заданного дерева.
| Лемма: |
Номер вершины встречается в коде Прюфера тогда и только тогда, когда не является листом или имеет номер . |
| Доказательство: |
|
| Лемма: |
По любой последовательности длины из чисел от до можно построить помеченное дерево,
для которого эта последовательность является кодом Прюфера. |
| Доказательство: |
|
Доказательство проведем по индукции. |
| Теорема: |
Кодирование Прюфера задаёт биекцию между множествами помеченных деревьев порядка и последовательностями длиной из чисел от до |
| Доказательство: |
|
Следствием из этой теоремы является формула Кэли.
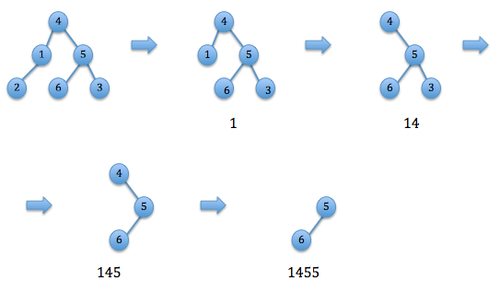
Пример построения кода Прюфера
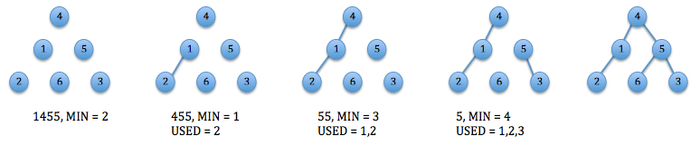
Пример декодирования кода Прюфера
Источники
Интернет Университет INTUIT | Представление с помощью списка ребер и кода Прюфера