Связь матрицы Кирхгофа и матрицы инцидентности — различия между версиями
Berkut (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Пусть <tex>G</tex> | + | Пусть <tex>G</tex> — произвольный граф. Превратим каждое его ребро в дугу, придав ребру одно из двух возможных направлений. Полученный [[ориентированный граф|орграф]] на том же самом множестве вершин будем называть '''ориентацией''' графа <tex>G</tex>. |
}} | }} | ||
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | Пусть <tex>K</tex> | + | Пусть <tex>K</tex> — [[Матрица Кирхгофа| матрица Кирхгофа]] графа <tex>G</tex>, <tex>I</tex> — [[Матрица инцидентности графа| матрица инцидентности]] <tex>G</tex> с некоторой ориентацией. Тогда |
<tex>K = I \cdot I^T.</tex> | <tex>K = I \cdot I^T.</tex> | ||
Версия 11:14, 11 декабря 2011
| Определение: |
| Пусть — произвольный граф. Превратим каждое его ребро в дугу, придав ребру одно из двух возможных направлений. Полученный орграф на том же самом множестве вершин будем называть ориентацией графа . |
| Лемма: |
Пусть — матрица Кирхгофа графа , — матрица инцидентности с некоторой ориентацией. Тогда
|
| Доказательство: |
| При умножении -й строки исходной матрицы на -й столбец транспонированной матрицы перемножаются -я и -я строки исходной матрицы. При умножении -й строки на саму себя на диагонали полученной матрицы получится сумма квадратов элементов -й строки, которая равна, очевидно, . Пусть теперь . Если , то существует ровно одно ребро, соединяющее и , следовательно результат перемножения -й и -й строк равен -1, в противном случае он равен 0 в силу отсутствия ребра, инцидентного обеим вершинам. Определенная данными условиями матрица и является матрицей Кирхгофа. |
| Граф | Матрица Кирхгофа | Матрица инцидентности |
|---|---|---|
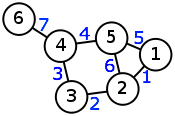
|
Источники
Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр.