Алгоритм Дейкстры — различия между версиями
Vasin (обсуждение | вклад) (→Псевдокод) |
Vasin (обсуждение | вклад) |
||
| Строка 17: | Строка 17: | ||
== Обоснование корректности == | == Обоснование корректности == | ||
| − | Пусть <tex>\rho(u, | + | {{Теорема |
| + | |statement= | ||
| + | Пусть <tex>G = (V, E)</tex> - ориентированный взвешенный граф, вес рёбер которого неотрицателен, <tex>s</tex> - стартовая вершина. | ||
| + | Тогда после выполнения алгоритма Дейкстры <tex>d(u) = \rho(s, u)</tex> для всех <tex>u</tex>, где <tex>\rho(s, u)</tex> — длина кратчайшего пути из вершины <tex>s</tex> в вершину <tex>u</tex> | ||
| + | |proof= | ||
| + | Докажем по индукции, что в момент посещения любой вершины <tex>u</tex>, <tex>d(u) = \rho(s, u)</tex>, где <tex>s</tex> - стартовая вершина. | ||
* На первом шаге выбирается <tex>s</tex>, для нее выполнено: <tex>d(s) = \rho(s, s) = 0</tex> | * На первом шаге выбирается <tex>s</tex>, для нее выполнено: <tex>d(s) = \rho(s, s) = 0</tex> | ||
* Пусть для <tex>n</tex> первых шагов алгоритм сработал верно и на <tex>n + 1</tex> шагу выбрана вершина <tex>u</tex>. Докажем, что в этот момент <tex>d(u) = \rho(s, u)</tex>. Для начала отметим, что для любой вершины <tex>v</tex>, всегда выполняется <tex>d(v) \ge \rho(s, v)</tex> (алгоритм не может найти путь короче, чем кратчайший из всех существующих). Пусть <tex>P</tex> — кратчайший путь из <tex>s</tex> в <tex>u</tex>, <tex>v</tex> — первая непосещённая вершина на <tex>P</tex>, <tex>z</tex> — предшествующая ей (следовательно, посещённая). Поскольку путь <tex>P</tex> кратчайший, его часть, ведущая из <tex>s</tex> через <tex>z</tex> в <tex>v</tex>, тоже кратчайшая, следовательно <tex>\rho(s, v) = \rho(s, z) + w(zv)</tex>. По предположению индукции, в момент посещения вершины <tex>z</tex> выполнялось <tex>d(z) = \rho(s, z)</tex>, следовательно, вершина <tex>v</tex> тогда получила метку не больше чем <tex>d(z) + w(zv) = \rho(s, z) + w(zv) = \rho(s, v)</tex>, следовательно, <tex>d(v) = \rho(s, v)</tex>. С другой стороны, поскольку сейчас мы выбрали вершину <tex>u</tex>, её метка минимальна среди непосещённых, то есть <tex>d(u) \le d(v) = \rho(s, v) \le \rho(s, u)</tex>, где второе неравенсто верно из-за ранее упомянутого определения вершины <tex>v</tex> в качестве первой непосещённой вершины на <tex>P</tex>, то есть вес пути до промежуточной вершины не превосходит веса пути до конечной вершины вследствие неотрицательности весовой функции. Комбинируя это с <tex>d(u) \ge \rho(s, u)</tex>, имеем <tex>d(u) = \rho(s, u)</tex>, что и требовалось доказать. | * Пусть для <tex>n</tex> первых шагов алгоритм сработал верно и на <tex>n + 1</tex> шагу выбрана вершина <tex>u</tex>. Докажем, что в этот момент <tex>d(u) = \rho(s, u)</tex>. Для начала отметим, что для любой вершины <tex>v</tex>, всегда выполняется <tex>d(v) \ge \rho(s, v)</tex> (алгоритм не может найти путь короче, чем кратчайший из всех существующих). Пусть <tex>P</tex> — кратчайший путь из <tex>s</tex> в <tex>u</tex>, <tex>v</tex> — первая непосещённая вершина на <tex>P</tex>, <tex>z</tex> — предшествующая ей (следовательно, посещённая). Поскольку путь <tex>P</tex> кратчайший, его часть, ведущая из <tex>s</tex> через <tex>z</tex> в <tex>v</tex>, тоже кратчайшая, следовательно <tex>\rho(s, v) = \rho(s, z) + w(zv)</tex>. По предположению индукции, в момент посещения вершины <tex>z</tex> выполнялось <tex>d(z) = \rho(s, z)</tex>, следовательно, вершина <tex>v</tex> тогда получила метку не больше чем <tex>d(z) + w(zv) = \rho(s, z) + w(zv) = \rho(s, v)</tex>, следовательно, <tex>d(v) = \rho(s, v)</tex>. С другой стороны, поскольку сейчас мы выбрали вершину <tex>u</tex>, её метка минимальна среди непосещённых, то есть <tex>d(u) \le d(v) = \rho(s, v) \le \rho(s, u)</tex>, где второе неравенсто верно из-за ранее упомянутого определения вершины <tex>v</tex> в качестве первой непосещённой вершины на <tex>P</tex>, то есть вес пути до промежуточной вершины не превосходит веса пути до конечной вершины вследствие неотрицательности весовой функции. Комбинируя это с <tex>d(u) \ge \rho(s, u)</tex>, имеем <tex>d(u) = \rho(s, u)</tex>, что и требовалось доказать. | ||
*Поскольку алгоритм заканчивает работу, когда все вершины посещены, в этот момент <tex>d(u) = \rho(s, u)</tex> для всех <tex>u</tex>. | *Поскольку алгоритм заканчивает работу, когда все вершины посещены, в этот момент <tex>d(u) = \rho(s, u)</tex> для всех <tex>u</tex>. | ||
| − | + | }} | |
== Оценка сложности == | == Оценка сложности == | ||
Основной цикл выполняется <tex>V</tex> раз. Релаксация выполниться всего <tex>E</tex> раз. В реализации алгоритма присутствует функция выбора вершины с минимальным значением <tex>d</tex>, асимптотика её работы зависит от реализации. | Основной цикл выполняется <tex>V</tex> раз. Релаксация выполниться всего <tex>E</tex> раз. В реализации алгоритма присутствует функция выбора вершины с минимальным значением <tex>d</tex>, асимптотика её работы зависит от реализации. | ||
Версия 09:18, 17 января 2012
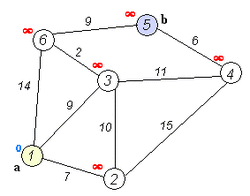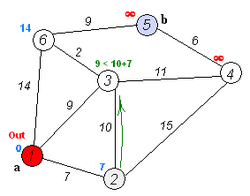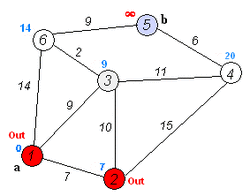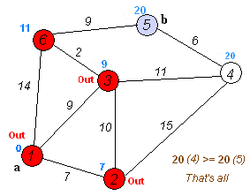
В ориентированном взвешенном графе , вес рёбер которого неотрицателен и определяется весовой функцией , алгоритм Дейкстры находит длины кратчайших путей из заданной вершины до всех остальных.
Содержание
[убрать]Алгоритм
В алгоритме поддерживается множество вершин , для которых уже вычислены длины кратчайших путей до них из . На каждой итерации основного цикла выбирается вершина , которой на текущий момент соответствует минимальная оценка кратчайшего пути. Вершина добавляется в множество и производится релаксация всех исходящих из неё рёбер.
Псевдокод
Для всех
Пока
-
Пустьминимальный -
Для всехтаких, что-
еслито
-
Обоснование корректности
| Теорема: |
Пусть - ориентированный взвешенный граф, вес рёбер которого неотрицателен, - стартовая вершина.
Тогда после выполнения алгоритма Дейкстры для всех , где — длина кратчайшего пути из вершины в вершину |
| Доказательство: |
|
Докажем по индукции, что в момент посещения любой вершины , , где - стартовая вершина.
|
Оценка сложности
Основной цикл выполняется раз. Релаксация выполниться всего раз. В реализации алгоритма присутствует функция выбора вершины с минимальным значением , асимптотика её работы зависит от реализации.
Таким образом:
| Структура данных | Время работы |
|---|---|
| Наивная реализация | |
| Двоичная куча | |
| Фибоначчиева куча |
Источники
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)
- Википедия — свободная энциклопедия