Линейный клеточный автомат, эквивалентность МТ — различия между версиями
| Строка 43: | Строка 43: | ||
Таким образом, при симуляции головка <tex>h</tex> будет двигаться, повторяя поведение головки соответствующей МТ, при этом менять состояние будут только клетки <tex>a, h, b, C_R, C_L</tex>, для которых необходимо определить функции перехода. Обозначим для них функцию перехода: если <tex>x_u, q_v</tex> {{---}} символ на ленте и состояние МТ, то переход будет иметь вид <tex>(x_u, q_v) = {x_p}X/q_q</tex>, где <tex>X</tex> {{---}} сдвиг влево <tex>L</tex> или вправо <tex>R</tex>. Состояния <tex>C_L</tex> и <tex>C_R</tex> необходимы для решения проблемы конца ленты: в общем случае машина Тьюринга работает с бесконечной лентой, в то время как поддержка начальной конфигурации построенного автомата конечна, и в некоторый момент пустые состояния закончатся. Чтобы этого не произошло, введены <tex>C_L</tex> и <tex>C_R</tex>, которые переводят спокойные клетки в состояния, соответствующие пустым символам ленты МТ. | Таким образом, при симуляции головка <tex>h</tex> будет двигаться, повторяя поведение головки соответствующей МТ, при этом менять состояние будут только клетки <tex>a, h, b, C_R, C_L</tex>, для которых необходимо определить функции перехода. Обозначим для них функцию перехода: если <tex>x_u, q_v</tex> {{---}} символ на ленте и состояние МТ, то переход будет иметь вид <tex>(x_u, q_v) = {x_p}X/q_q</tex>, где <tex>X</tex> {{---}} сдвиг влево <tex>L</tex> или вправо <tex>R</tex>. Состояния <tex>C_L</tex> и <tex>C_R</tex> необходимы для решения проблемы конца ленты: в общем случае машина Тьюринга работает с бесконечной лентой, в то время как поддержка начальной конфигурации построенного автомата конечна, и в некоторый момент пустые состояния закончатся. Чтобы этого не произошло, введены <tex>C_L</tex> и <tex>C_R</tex>, которые переводят спокойные клетки в состояния, соответствующие пустым символам ленты МТ. | ||
| − | |||
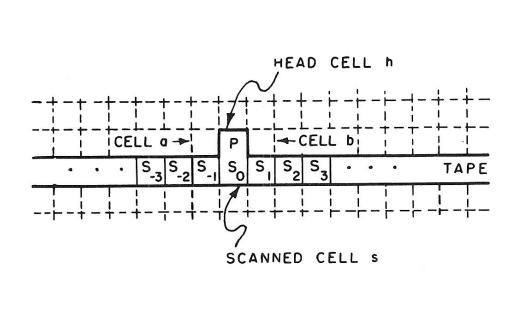
[[Изображение:Tape.jpg|640px|thumb|center|Рис. 2. Эмуляция ленты МТ в КА]] | [[Изображение:Tape.jpg|640px|thumb|center|Рис. 2. Эмуляция ленты МТ в КА]] | ||
| Строка 52: | Строка 51: | ||
Также определим в каждой клетке состояние <tex>w</tex>, соответствующее начальному состоянию МТ. Перед началом эмуляции клетки ленты переведем в состояния, эквивалентные входным символам, клетку над самой левой непустой клеткой ленты переведем в состояние <tex>w</tex>, которая будет соответствовать начальному положению головки. Тогда клетки ленты будут менять свои состояние так же, как лента МТ. | Также определим в каждой клетке состояние <tex>w</tex>, соответствующее начальному состоянию МТ. Перед началом эмуляции клетки ленты переведем в состояния, эквивалентные входным символам, клетку над самой левой непустой клеткой ленты переведем в состояние <tex>w</tex>, которая будет соответствовать начальному положению головки. Тогда клетки ленты будут менять свои состояние так же, как лента МТ. | ||
| + | }} | ||
| + | |||
| + | {{Теорема | ||
| + | |definition=Для произвольной <tex>(m, n)</tex> машины Тьюринга существует линейный КА с окрестность не более, чем из шести клеток, <tex>max(m + 1, n + 1)</tex> состояниями, эмулирующий эту МТ в реальном времени. | ||
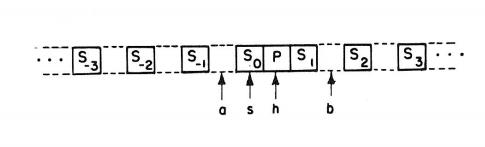
| + | |proof=Аналогично предыдущей теореме. Лента будет иметь следующий вид: | ||
| + | [[Изображение:Tape2.jpg|640px|thumb|center|Рис. 2. Эмуляция ленты МТ в ЛКА]] | ||
| + | }} | ||
Версия 00:22, 24 января 2012
Определения
| Определение: |
Клеточным автоматом (КА) размерности называется четверка , где
|
| Определение: |
| Линейным клеточным автоматом (ЛКА) называется одномерный клеточный автомат, окрестность каждой клетки которого состоит из клеток, находящихся на расстоянии не более от данной. |
| Определение: |
| Состоянием покоя (quiescent state) называется такое состояние клетки, что если клетка и все ее соседи находятся в состояниях покоя, то они в них останутся. |
| Определение: |
| Спокойной клеткой (quiescent cell) назовем клетку, автомат в которой перешел в состояние покоя. |
| Определение: |
| Конфигурацией (configuraton) КА называется распределение состояний автоматов по клеточному пространству, где — шаг, после которого была получена конфигурация. Начальная конфиграция — . |
| Определение: |
| Поддержкой (support) конфигурации называется множество неспокойных клеток в ней. Обозначается . |
Другое определение линейного клеточного автомата
| Определение: |
| Линейным клеточным автоматом назовем бесконечную ленту, в каждой клетке которой записан некоторый автомат. На вход автомату в клетке подается вектор из состояний автоматов в клетках с по включительно. |
| Лемма: |
Для любого ЛКА можно построить эквивалентный ему ЛКА, во всех клетках которого будет записан один и тот же автомат. |
| Доказательство: |
| Так как окрестность каждой клетки конечна и размер автомата в клетке конечен, то всего существует конечное число автоматов. Обозначим их множество как . Построим автомат следующим образом: множеством вершин будет объединение множеств вершин автоматов из , переходы между вершинами и будет совпадать с переходами , если и соответствуют вершинам из , иначе переход отсутствует. Начальным состоянием автомата будет состояние,соответствующее начальному состоянию автомата , который был записан в текущей клетке. Очевидно, что поведение такого автомата будет совпадать с поведением . |
Эквивалентность линейного клеточного автомата машине Тьюринга
| Теорема: |
Для произвольной (m, n) машины Тьюринга существует двумерный КА с окрестностью из семи клеток и клеточным пространством с состояниями, симулирующий ее в реальном времени. |
| Доказательство: |
|
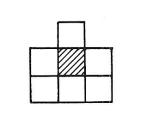
Каждая клетка обладает множеством из состояний. Без потери общности, будем считать, что , так что будет сопоставляться символу машины Тьюринга при , а состояние будет соответствовать состоянию машины Тьюринга при . Ноль является состоянием покоя и не будет соответствовать символам и состояниям машины Тьюринга. Окрестность построим таким образом, чтобы выделять клетку, состояние которой будет соответствовать символу машины Тьюринга из клетки, состояние которой соответствует состоянию машины Тьюринга (окрестность клетки в таком КА показана на Рис. 1).
Таким образом, симулирует машину Тьюринга, используя конфигурацию, в которой оно выглядит как машина Тьюринга. Один ряд клеток в представляет из себя ленту машины Тьюринга — одна клетка для каждой клетки ленты, а одна клетка из соседнего ряда будет соответствовать головке МТ, и в каждый момент времени автомат будет выглядеть так, как показано на рисунке ниже. Клетки и всегда указывают на клетки слева и справа от головки соответственно. Все остальные символы используются для хранения состояний: обозначает состояние клетки ленты на расстоянии от головки по направлению знака индекса, обозначает состояние головки. Клетки справа и слева от головки обозначим и , которые будут определять правый или левый конец использованной ленты. Все клетки кроме и клеток ленты будут находится в состоянии покоя ноль. Таким образом, при симуляции головка будет двигаться, повторяя поведение головки соответствующей МТ, при этом менять состояние будут только клетки , для которых необходимо определить функции перехода. Обозначим для них функцию перехода: если — символ на ленте и состояние МТ, то переход будет иметь вид , где — сдвиг влево или вправо . Состояния и необходимы для решения проблемы конца ленты: в общем случае машина Тьюринга работает с бесконечной лентой, в то время как поддержка начальной конфигурации построенного автомата конечна, и в некоторый момент пустые состояния закончатся. Чтобы этого не произошло, введены и , которые переводят спокойные клетки в состояния, соответствующие пустым символам ленты МТ. Функция перехода имеет следующий вид: Также определим в каждой клетке состояние , соответствующее начальному состоянию МТ. Перед началом эмуляции клетки ленты переведем в состояния, эквивалентные входным символам, клетку над самой левой непустой клеткой ленты переведем в состояние , которая будет соответствовать начальному положению головки. Тогда клетки ленты будут менять свои состояние так же, как лента МТ. |
| Теорема: |
{{{statement}}} |
| Доказательство: |
|
Аналогично предыдущей теореме. Лента будет иметь следующий вид: |