Матрица инцидентности графа — различия между версиями
(→Инцидентность ребра и вершины) |
|||
| Строка 3: | Строка 3: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Инцидентность''' - отношение между ребром и его концевыми вершинами, т. е. если в графе <tex>G = (V,E), u \in V, v \in V</tex> - вершины, а <tex>e \in E, e = (u,v)</tex> - соединяющее их ребро, то вершина <tex>u</tex> и ребро <tex>e</tex> инцидентны, вершина <tex>v</tex> и ребро <tex>e</tex> также инцидентны. | + | '''Инцидентность''' {{---}} отношение между ребром и его концевыми вершинами, т. е. если в графе <tex>G = (V,E), u \in V, v \in V</tex> {{---}} вершины, а <tex>e \in E, e = (u,v)</tex> {{---}} соединяющее их ребро, то вершина <tex>u</tex> и ребро <tex>e</tex> инцидентны, вершина <tex>v</tex> и ребро <tex>e</tex> также инцидентны. |
}} | }} | ||
| Строка 45: | Строка 45: | ||
==Источники== | ==Источники== | ||
| − | Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы | + | Асанов М., Баранский В., Расин В. {{---}} Дискретная математика: Графы, матроиды, алгоритмы {{---}} Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр. |
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Основные определения теории графов]] | [[Категория: Основные определения теории графов]] | ||
Версия 07:56, 3 февраля 2012
Содержание
Инцидентность ребра и вершины
| Определение: |
| Инцидентность — отношение между ребром и его концевыми вершинами, т. е. если в графе — вершины, а — соединяющее их ребро, то вершина и ребро инцидентны, вершина и ребро также инцидентны. |
Определения для ориентированного и неориентированного графов
| Определение: |
| Матрицей инцидентности (инциденций) неориентированного графа называется матрица , для которой , если вершина инцидентна ребру , в противном случае . |
| Определение: |
| Матрицей инцидентности (инциденций) ориентированного графа называется матрица , для которой , если вершина является началом дуги , , если является концом дуги , в остальных случаях . |
Пример
| Граф | Матрица инцидентности | Ориентированный граф | Матрица инцидентности |
|---|---|---|---|
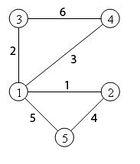
|
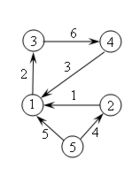
|
Источники
Асанов М., Баранский В., Расин В. — Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр.