Алгоритм Хаффмана

Алгоритм Хаффмана — алгоритм оптимального префиксного кодирования алфавита. Это один из классических алгоритмов, известных с 60-х годов. Использует только частоту появления одинаковых байт в изображении. Сопоставляет символам входного потока, которые встречаются большее число раз, цепочку бит меньшей длины. И, напротив, встречающимся редко — цепочку большей длины.

Определение

Определение:

Пусть [math]A=\{a_{1},a_{2},...,a_{n}\}[/math] — алфавит из n различных символов, [math]W=\{w_{1},w_{2},...,w_{n}\}[/math] — соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов [math]C=\{c_{1},c_{2},...,c_{n}\}[/math], такой, что: 1. [math]c_{i}[/math] не является префиксом для [math]c_{j}[/math], при [math]i \ne j[/math] 2. Сумма [math]\sum\limits_{i \in [1, n]} w_{i}\cdot c_{i}[/math] минимальна. ([math]|c_{i}|[/math] — длина кода [math]c_{i}[/math]) называется кодом Хаффмана.

Алгоритм

Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:

1. Составим список кодируемых символов, при этом будем рассматривать один символ как дерево, состоящее из одного элемента, весом, равным частоте появления символа в тексте.

2. Из списка выберем два узла с наименьшим весом.

3. Сформируем новый узел с весом, равным сумме весов выбранных узлов, и присоединим к нему два выбранных узла в качестве дочерних.

4. Добавим к списку только что сформированный узел.

5. Если в списке больше одного узла, то повторить пункты со второго по пятый.

Пример

Дерево Хаффмана для слова "Миссисипи"

Для примера возьмём слово "Миссисипи". Тогда алфавит будет [math]A= \{[/math] и, м, п, с [math]\} [/math], а набор весов [math]W=\{4, 1, 1, 3\}[/math]:

Узел	и	м	п	с
Вес	4	1	1	3

По алгоритму возьмем два символа с наименьшей частотой - это м и п. Сформируем из них новый узел мп весом 2 и добавим его к списку узлов:

Узел	и	мп	с
Вес	4	2	3

Затем объединим в один узел узлы мп и c:

Узел	и	мпс
Вес	4	5

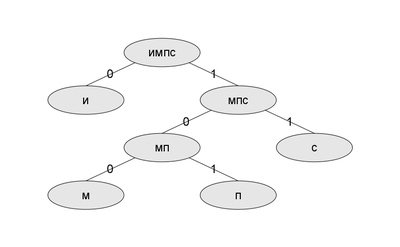
И, наконец, объединяем два узла и и мпс. Итак, мы получили дерево Хаффмана и соответствующую ему таблицу кодов:

Символ	и	м	п	с
Код	0	100	101	11

Таким образом, закодированное слово "миссисипи" будет выглядеть как "1000111101101010". Длина закодированного слова - 16 бит. Стоит заметить, что если бы мы использовали для кодирования каждого символа из четырёх по 2 бита, длина закодированного слова составила бы 18 бит.

Корректность алгоритма Хаффмана

Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.

Лемма (1):

Пусть [math]C[/math] — алфавит, каждый символ [math]c \in C[/math] которого встречается с частотой [math]f[c][/math]. Пусть [math]x[/math] и [math]y[/math] — два символа алфавита [math]C[/math] с самыми низкими частотами. Тогда для алфавита [math]C[/math] существует оптимальный префиксный код, кодовые слова символов [math]x[/math] и [math]y[/math] в котором имеют одинаковую максимальную длину и отличаются лишь последним битом.

Доказательство:

[math]\triangleright[/math]

Возьмем дерево [math]T[/math], представляющее произвольный оптимальный префиксный код для алфавита [math]C[/math]. Преобразуем его в дерево, представляющее другой оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] - листья с общим родительским узлом, находящиеся на максимальной глубине. Пусть символы [math]a[/math] и [math]b[/math] имеют общий родительский узел и находятся на максимальной глубине дерева [math]T[/math]. Предположим, что [math]f[a] \le f[b][/math] и [math]f[x] \le f[y][/math]. Так как [math]f[x][/math] и [math]f[y][/math] - две наименьшие частоты, а [math]f[a][/math] и [math]f[b][/math] - две произвольные частоты, то выполняются отношения [math]f[x] \le f[a][/math] и [math]f[y] \le f[b][/math]. Пусть дерево [math]T'[/math] - дерево, полученное из [math]T[/math] путем перестановки листьев [math]a[/math] и [math]x[/math], а дерево [math]T''[/math] - дерево полученное из [math]T'[/math] перестановкой листьев [math]b[/math] и [math]y[/math]. Разность стоимостей деревьев [math]T[/math] и [math]T'[/math] равна: [math]B(T) - B(T') = \sum\limits_{c \in C} f(c)d_T(c) - \sum\limits_{c \in C} f(c)d_{T'}(c) = (f[a] - f[x])(d_T(a) - d_T(x)),[/math] что больше либо равно [math]0[/math], так как величины [math]f[a] - f[x][/math] и [math]d_T(a) - d_T(x)[/math] неотрицательны. Величина [math]f[a] - f[x][/math] неотрицательна, потому что [math]x[/math] - лист с минимальной частотой, а величина [math]d_T(a) - d_T(x)[/math] является неотрицательной, так как лист [math]a[/math] находится на максимальной глубине в дереве [math]T[/math]. Точно так же перестановка листьев [math]y[/math] и [math]b[/math] не будет приводить к увеличению стоимости. Таким образом, разность [math]B(T') - B(T'')[/math] тоже будет неотрицательной. Таким образом, выполняется неравенство [math]B(T'') \le B(T)[/math]. С другой стороны, [math]T[/math] - оптимальное дерево, поэтому должно выполняться неравенство [math]B(T) \le B(T'')[/math]. Отсюда следует, что [math]B(T) = B(T'')[/math]. Значит, [math]T''[/math] - дерево, представляющее оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] имеют одинаковую максимальную длину, что и доказывает лемму.

[math]\triangleleft[/math]

Лемма (2):

Пусть дан алфавит [math]C[/math], в котором для каждого символа [math]c \in C[/math] определены частоты [math]f[c][/math]. Пусть [math]x[/math] и [math]y[/math] — два символа из алфавита [math]C[/math] с минимальными частотами. Пусть [math]C'[/math] — алфавит, полученный из алфавита [math]C[/math] путем удаления символов [math]x[/math] и [math]y[/math] и добавления нового символа [math]z[/math], так что [math]C' = C \backslash \{ x, y \} \cup {z}[/math]. По определению частоты [math]f[/math] в алфавите [math]C'[/math] совпадают с частотами в алфавите [math]C[/math], за исключением частоты [math]f[z] = f[x] + f[y][/math]. Пусть [math]T'[/math] — произвольное дерево, представляющее оптимальный префиксный код для алфавита [math]C'[/math] Тогда дерево [math]T[/math], полученное из дерева [math]T'[/math] путем замены листа [math]z[/math] внутренним узлом с дочерними элементами [math]x[/math] и [math]y[/math], представляет оптимальный префиксный код для алфавита [math]C[/math].

Доказательство:

[math]\triangleright[/math]

Сначала покажем, что стоимость [math]B(T)[/math] дерева [math]T[/math] можно выразить через стоимость [math]B(T')[/math] дерева [math]T'[/math]. Для каждого символа [math]c \le C \backslash \{x,y\}[/math] выполняется соотношение [math]d_T(C) = d_{T'}(c)[/math], следовательно, [math]f[c]d_T(C) = f[c]d_{T'}(c)[/math]. Поскольку [math]d_T(x) = d_{T}(y) = d_{t'}(z) + 1[/math], получаем соотношение [math]f[x]d_T(x) + f[y]d_{T}(y) = (f[x] + f[y])(d_{T'}(z) + 1) = f[z]d_{T'}(z) + (f[x] + f[y])[/math] из которого следует равенство [math] B(T) = B(T') + f[x] + f[y] [/math] или [math] B(T') = B(T) - f[x] - f[y] [/math]. Докажем лемму методом от противного. Предположим, дерево [math] T [/math] не представляет оптимальный префиксный код для алфавита [math] C [/math]. Тогда существует дерево [math] T'' [/math], для которого справедливо неравенство [math] B(T'') \lt B(T) [/math]. Согласно лемме (1), [math]x[/math] и [math]y[/math] без потери общности можно считать дочерними элементами одного и того же узла. Пусть дерево [math]T'''[/math] получено из дерева [math]T''[/math] путем замены элементов [math]x[/math] и [math]y[/math] листом [math]z[/math] с частотой [math]f[z] = f[x] + f[y] [/math]. Тогда можно записать: [math]B(T''') = B(T'') - f[x] - f[y] \lt B(T) - f[x] -f[y] = B(T')[/math], что противоречит предположению о том, что дерево [math]T'[/math] представляет оптимальный префиксный код для алфавита [math]C'[/math]. Таким образом, дерево [math]T[/math] должно представлять оптимальный префиксный код для алфавита [math]C[/math].

[math]\triangleleft[/math]

Теорема:

Алгоритм Хаффмана дает оптимальный префиксный код.

Доказательство:

[math]\triangleright[/math]

Справедливость теоремы непосредственно следует из лемм (1) и (2)

[math]\triangleleft[/math]

Литература

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4