Алгоритм масштабирования потока — различия между версиями
(→Корректность алгоритма) |
(→Алгоритм) |
||
| Строка 6: | Строка 6: | ||
На каждой итерации в [[Дополняющая_сеть,_дополняющий_путь|дополняющей сети]] находим дополняющие пути с пропускной способностью не меньшей <tex> \Delta </tex>, увеличиваем поток вдоль них. | На каждой итерации в [[Дополняющая_сеть,_дополняющий_путь|дополняющей сети]] находим дополняющие пути с пропускной способностью не меньшей <tex> \Delta </tex>, увеличиваем поток вдоль них. | ||
Уменьшив масштаб <tex> \Delta </tex> в <tex> 2 </tex> раза, переходим к следующей итерации. | Уменьшив масштаб <tex> \Delta </tex> в <tex> 2 </tex> раза, переходим к следующей итерации. | ||
| + | |||
| + | Заметим, что при <tex> \Delta = 1 </tex> алгоритм вырождается в алгоритм [[Алоритм_Эдмондса-Карпа|Эдмондса-Карпа]], вследствие чего является корректным. | ||
Количество необходимых дополнений путей, основанных на кратчайших путях, может быть много больше количества дополнений, основанных на путях с высокой пропускной способностью. | Количество необходимых дополнений путей, основанных на кратчайших путях, может быть много больше количества дополнений, основанных на путях с высокой пропускной способностью. | ||
Версия 02:31, 29 февраля 2012
Содержание
Алгоритм
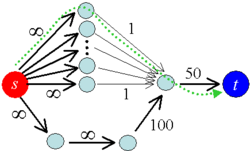
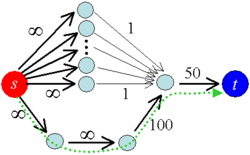
Пусть дана сеть , все ребра которой имеют целочисленную пропускную способность. Обозначим за максимальную пропускную способность: .
Идея алгоритма заключается в нахождении путей с высокой пропускной способностью в первую очередь, чтобы сразу сильно увеличивать поток по ним, а затем по всем остальным. Для этого воспользуемся масштабом . Изначально положим .
На каждой итерации в дополняющей сети находим дополняющие пути с пропускной способностью не меньшей , увеличиваем поток вдоль них. Уменьшив масштаб в раза, переходим к следующей итерации.
Заметим, что при алгоритм вырождается в алгоритм Эдмондса-Карпа, вследствие чего является корректным.
Количество необходимых дополнений путей, основанных на кратчайших путях, может быть много больше количества дополнений, основанных на путях с высокой пропускной способностью.
Оценка времени работы
| Утверждение: | ||||||||||||||||||
Время работы алгоритма — . | ||||||||||||||||||
|
Пусть — множество масштабов. Тогда — количество итераций алгоритма.
| ||||||||||||||||||
Псевдокод
Max_Flow_By_Scaling(G,s,t)
while
do while в существует увеличивающий путь с пропускной способностью не меньшей
do
увеличить поток по рёбрам на
обновить
return