Упрощение полигональной цепи

Упрощение полигональной цепи — процесс, позволяющий уменьшить число точек кривой, аппроксимированной серией точек.

Задача

Дана некоторая аппроксимированная кривая, заданная последовательностью точек, и некоторое [math]\varepsilon[/math]. Требуется ответить, какие точки мы можем оставить, так чтобы расхождение между исходной и получившейся кривыми не превышало [math]\varepsilon[/math], при этом количество точек в получившейся кривой должно стремиться к минимуму.

Мотивация

Такая задача встречается при обработки векторной графики и построении карт. Расмотрим пример для построения карт. Дан путь из Москвы в Санкт-Петербург, заданный точками через каждый километр пути. В масштабах всей России такая точность явно ни к чему, стоит оставить лишь точки, отражающие ключевые участки пути. В этом случае и пригодится упрощение, одним из вариантов реализации которого является алгоритм Дугласа-Пекера.

Алгоритм Дугласа-Пекера

Алгоритму задается исходная ломаная и максимальное расстояние, которое может быть между исходной и упрощённой ломаными (то есть максимальное расстояние от точек исходной ломаной к ближайшему участку полученной ломаной). Упрощенная ломаная состоит из подмножества точек, которые определяются из исходной ломаная.

Описание

Начальная ломаная представляет собой упорядоченный набор точек.

Алгоритм рекурсивно делит ломаную. Входом алгоритма служат координаты всех точек между первой и последней включая их, а так же [math]\varepsilon[/math]. Первая и последняя точка сохраняются неизменными. После чего алгоритм находит точку, наиболее удалённую от отрезка, состоящего из первой и последней (оптимальный способ поиска расстояния от точки до отрезка рассмотрен ниже). Если точка находится на расстоянии, меньше чем [math]\varepsilon[/math], то все точки, которые ещё не были отмечены к сохранению, могут быть выброшены из набора и получившаяся прямая сглаживает кривую с точностью не ниже [math]\varepsilon[/math].

Если же расстояние больше [math]\varepsilon[/math], то алгоритм рекурсивно вызывает себя на наборе от начальной до данной и от данной до конечной точек (что означает, что данная точка будет отмечена к сохранению).

По окончанию всех рекурсивных вызовов выходная ломаная строится только из тех точек, что были отмечены к сохранению.

Псевдокод

DouglasPeucker(int first, int last, double eps)

max = -infinity

index = -1

for (int i = first + 1; i < last; i++)

distance = dist(points[i], segment(points[first],points[last]))

if (distance > max && distance > eps)

max = distance, index = i

if(index == -1)

return

else

answer[index] = true

DouglasPeucker(first, index, eps)

DouglasPeucker(index, last, eps)

Пример

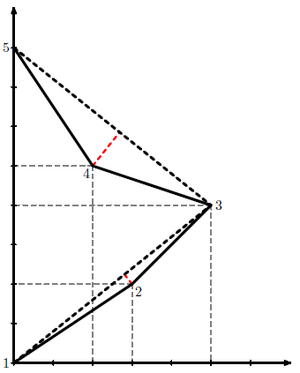
Рассмотрим пример для точек, заданных на рисунке, где сплошная линия отражает исходную линию, и [math]\varepsilon = \sqrt 2[/math].

Шаг	Действие
[math]1[/math]	Найдем наиболее удаленную точку от отрезка [math]1-5[/math], это точка [math]3[/math]
[math]2[/math]	Расстояние до точки [math]3[/math] больше [math]\sqrt 2[/math], добавляем ее в ответ
[math]3[/math]	Запустим алгоритм для точек [math]1[/math] и [math]3[/math]
[math]4[/math]	Найдем наиболее удаленную точку от отрезка [math]1-3[/math], это точка [math]2[/math]
[math]5[/math]	Расстояние до точки [math]2[/math] меньше [math]\sqrt 2[/math], возвращаемся
[math]6[/math]	Запустим алгоритм для точек [math]3[/math] и [math]5[/math]
[math]7[/math]	Найдем наиболее удаленную точку от отрезка [math]3-5[/math], это точка [math]4[/math]
[math]8[/math]	Расстояние до точки [math]4[/math] меньше [math]\sqrt 2[/math], возвращаемся
[math]9[/math]	Алгоритм завершен

Линия, полученная в результате работы алгоритма, отражается пунктирной линией.

Время работы

Ожидаемая сложность алгоритма может быть оценена выражением [math]\Theta(n\log n)[/math] в лучшем случае, когда номер наиболее удаленной точки всегда оказывается лексикографически центральным. Однако в худшем случае сложность алгоритма [math]O\left(n^2\right)[/math], когда номер наиболее удаленной точки всегда соседний к номеру граничащей точки.

Замечания к алгоритму

Топология

К сожалению, алгоритм Дугласа-Пекера в ходе своей работы не сохраняет топологию, что означает в ответе мы можем получить линию с самопересечениями.

Оптимальность

Оптимальный по количеству точек ответ

Ответ алгоритма Дугласа-Пекера

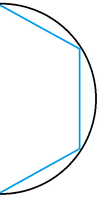
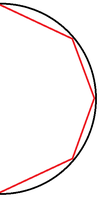
Алгоритм может находить не минимальный по количеству точек ответ. Рассмотрим пример, где исходная линия с некоторым приближением будет представлять полуокружность. Мы можем подобрать такое [math]\varepsilon[/math], что алгоритм добавит три точки помимо стартовой и конечной (точки через каждую четверть исходной линии), в то же время мы можем взять две точки через каждую треть исходной линии, для которых упрощение также верно.

Поиск расстояния от точки до отрезка

Идея

При определении расстояния от точки до отрезка нужно сначала проанализировать взаимное расположение точки и отрезка прямой, то есть, проверить, куда опустится перпендикуляр из точки: непосредственно на отрезок или на прямую, являющуюся продолжением рассматриваемого отрезка.

Если на отрезок, то ответ это расстояние от исходной точки до точки пересечения отрезка с перпендикуляром, если нет, то расстояние от исходной точки до одного из концов отрезка.

Самое очевидное — это найти точку пересечения перпендикуляра и прямой, и в зависимости от ее положения вычислить ответ. На самом деле, этот анализ может быть произведен путем построения треугольника, вершинами которого являются концы отрезка и точка, и сопоставления соотношения длин его сторон.

Реализация

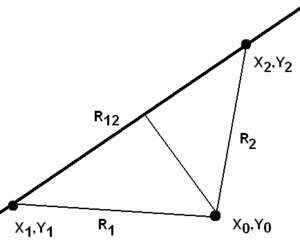
Даны точка [math](x_0, y_0)[/math] и отрезок, заданный точками [math](x_1, y_1)[/math] и [math](x_2, y_2)[/math].

Введём обозначения:

• [math]R_1[/math] отрезок [math](x_0, y_0)[/math][math](x_1, y_1)[/math]
• [math]R_2[/math] отрезок [math](x_0, y_0)[/math][math](x_2, y_2)[/math]
• [math]R_{12}[/math] отрезок [math](x_1, y_1)[/math][math](x_2, y_2)[/math]

Если:

• [math]|R_1| \ge \sqrt{|R_2|^2+|R_{12}|^2}[/math], то ответ это [math]|R_2|[/math], так как угол между [math]R_2[/math] и [math]R_{12}[/math] при данном условии [math] \ge 90^{\circ}[/math]
• [math]|R_2| \ge \sqrt{|R_1|^2+|R_{12}|^2}[/math], то ответ это [math]|R_1|[/math], так как угол между [math]R_1[/math] и [math]R_{12}[/math] при данном условии [math] \ge 90^{\circ}[/math]
• Оба предыдущих условия ложны, то [math]abs(| \overrightarrow{R_{12}} \times \overrightarrow{R_1}|/|\overrightarrow{R_{12}}|)[/math], где [math] \overrightarrow{R_{12}} = (x_2 -x_1, y_2 - y_1)[/math] и [math] \overrightarrow{R_1} = (x_1 - x_0, y_1 - y_0)[/math]. Это следует из формул для площади параллелограмма через векторное произведение и через произведения основания на высоту

Ссылки

• Алгоритм Дугласа-Пекера
• Поиск расстояния от точки до отрезка
• Поиск расстояния от точки до прямой