Биномиальная куча — различия между версиями
Gr1n (обсуждение | вклад) |
Gr1n (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
|neat = 1 | |neat = 1 | ||
|definition = | |definition = | ||
| − | '''Биномиальное дерево <tex>B_k</tex>''' {{---}} [[Дерево, эквивалентные определения|дерево]], определяемое для каждого <tex>k = 0, 1, 2, \dots </tex> следующим образом: <tex>B_0</tex> - дерево, состоящее из одного узла высоты 0, то есть состоит из одного узла; <tex>B_k</tex> состоит из двух биномиальных деревьев <tex>B_{k-1}</tex>, связанны вместе таким образом, что корень одного из них является крайним левым дочерним узлом корня второго дерева. | + | '''Биномиальное дерево <tex>B_k</tex>''' {{---}} [[Дерево, эквивалентные определения|дерево]], определяемое для каждого <tex>k = 0, 1, 2, \dots </tex> следующим образом: <tex>B_0</tex> - дерево, состоящее из одного узла высоты <tex>0</tex>, то есть состоит из одного узла; <tex>B_k</tex> состоит из двух биномиальных деревьев <tex>B_{k-1}</tex>, связанны вместе таким образом, что корень одного из них является крайним левым дочерним узлом корня второго дерева. |
}} | }} | ||
| Строка 10: | Строка 10: | ||
Биномиальное дерево <tex>B_k</tex> с n вершинами: | Биномиальное дерево <tex>B_k</tex> с n вершинами: | ||
*имеет <tex>2^k</tex> узлов; | *имеет <tex>2^k</tex> узлов; | ||
| − | *имеет высоту k; | + | *имеет высоту <tex>k</tex>; |
*имеет ровно <tex>{k\choose i}</tex> узлов на высоте <tex>i = 0, 1, 2, \dots</tex>; | *имеет ровно <tex>{k\choose i}</tex> узлов на высоте <tex>i = 0, 1, 2, \dots</tex>; | ||
| − | *имеет корень степени k; степерь всех остальных вершин меньше степени корня биномиального дерева; | + | *имеет корень степени <tex>k</tex>; степерь всех остальных вершин меньше степени корня биномиального дерева; |
*максимальная степень произвольного узла в биномиальном дереве с n узлами равна <tex>\log(n)</tex>. | *максимальная степень произвольного узла в биномиальном дереве с n узлами равна <tex>\log(n)</tex>. | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Биномиальная пирамида ([[Двоичная куча|куча]]) H''' {{---}} представляет собой множество биномиальных деревьев, которые удовлетворяют следующим свойствам '''биномиальных пирамид'''. | + | '''Биномиальная пирамида ([[Двоичная куча|куча]]) <tex>H</tex>''' {{---}} представляет собой множество биномиальных деревьев, которые удовлетворяют следующим свойствам '''биномиальных пирамид'''. |
| − | *Каждое биномиальное дерево в | + | *Каждое биномиальное дерево в <tex>H</tex> подчиняется свойству '''неубывающей пирамиды''': ключ узла не меньше ключа его родительского узла (упорядоченное в соответствии со свойством неубывающей пирамиды дерево). |
| − | *Для любого неотрицательного целого k найдется не более одного биномиального дерева | + | *Для любого неотрицательного целого <tex>k</tex> найдется не более одного биномиального дерева <tex>H</tex>, чей корень имеет степень <tex>k</tex>.}} |
==== Представление биномиальных куч ==== | ==== Представление биномиальных куч ==== | ||
Поскольку количество детей у узлов варьируется в широких пределах, ссылка на детей осуществляется через левого ребенка, а остальные дети образуют односвязный список. Каждый узел в биномиальной пирамиде (куче) представляется набором полей: | Поскольку количество детей у узлов варьируется в широких пределах, ссылка на детей осуществляется через левого ребенка, а остальные дети образуют односвязный список. Каждый узел в биномиальной пирамиде (куче) представляется набором полей: | ||
| − | * | + | *<tex>key</tex> {{---}} ключ (вес) элемента; |
| − | * | + | *<tex>parent</tex> {{---}} указатель на родителя узла; |
| − | * | + | *<tex>child</tex> {{---}} указатель на левого ребенка узла; |
| − | * | + | *<tex>sibling</tex> {{---}} указатель на правого брата узла; |
| − | * | + | *<tex>degree</tex> {{---}} степень узла (количество дочерних узлов данного узла). |
Корни деревьев, их которых состоит пирамида, содержатся в так называемом '''списке корней''', при проходе по которому степени соответствующих корней находятся в неубывающем порядке. | Корни деревьев, их которых состоит пирамида, содержатся в так называемом '''списке корней''', при проходе по которому степени соответствующих корней находятся в неубывающем порядке. | ||
Версия 20:15, 6 марта 2012
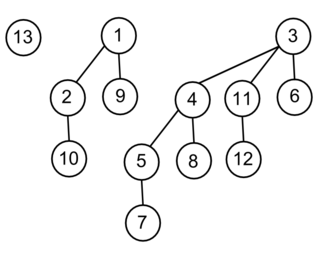
Свойства биномиальных деревьев. Биномиальное дерево с n вершинами:
- имеет узлов;
- имеет высоту ;
- имеет ровно узлов на высоте ;
- имеет корень степени ; степерь всех остальных вершин меньше степени корня биномиального дерева;
- максимальная степень произвольного узла в биномиальном дереве с n узлами равна .
| Определение: |
Биномиальная пирамида (куча) — представляет собой множество биномиальных деревьев, которые удовлетворяют следующим свойствам биномиальных пирамид.
|
Содержание
Представление биномиальных куч
Поскольку количество детей у узлов варьируется в широких пределах, ссылка на детей осуществляется через левого ребенка, а остальные дети образуют односвязный список. Каждый узел в биномиальной пирамиде (куче) представляется набором полей:
- — ключ (вес) элемента;
- — указатель на родителя узла;
- — указатель на левого ребенка узла;
- — указатель на правого брата узла;
- — степень узла (количество дочерних узлов данного узла).
Корни деревьев, их которых состоит пирамида, содержатся в так называемом списке корней, при проходе по которому степени соответствующих корней находятся в неубывающем порядке. Доступ к куче осуществляется ссылкой на первый корень в списке корней.
Операции над биномиальными пирамидами
Рассмотрим операции, которые можно производить с биномиальной пирамидой. Их асимптотические оценки показаны в таблице.
| makeHeap | |
| insert | |
| getMinimum | |
| extractMin | |
| merge | |
| decreaseKey | |
| delete |
makeHeap
Для создания пустой биномиальной пирамиды процедура makeBinomialHeap просто выделяет память и возвращает объект H, где head[H] = null, то есть пирамида не содержит элементов.
getMinimum
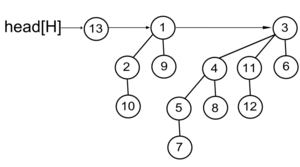
Для нахождения минимального элемента надо найти элемент в списке корней с минимальным значением (предполагается, что ключей, равных , нет).
Асимптотика этой операции получается из того, что корней в этом списке не более .
При вызове этой процедуры для кучи, изображенной на картинке ниже, будет возвращен указатель на вершину с ключем 1.
merge
Эта операция, соединяющая две биномиальные кучи в одну, используется в качестве подпрограммы большинством остальных операций.
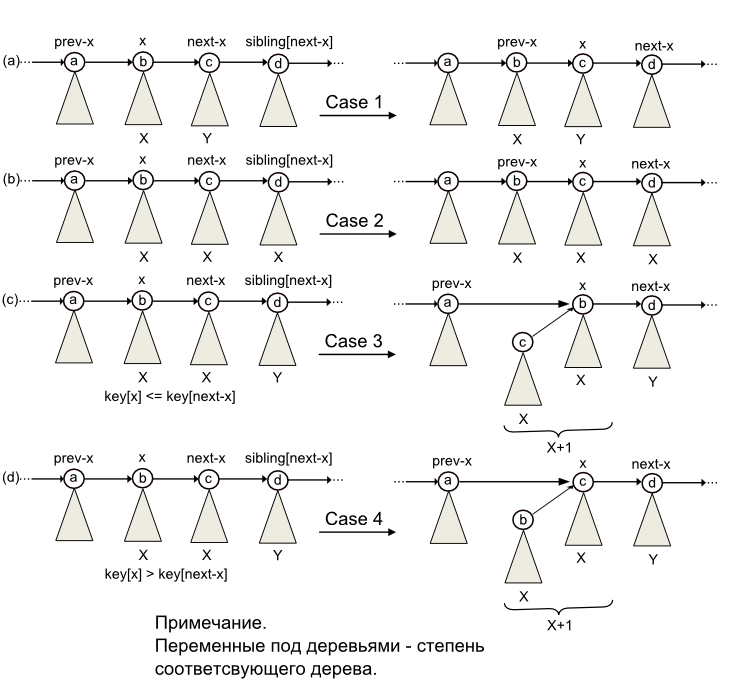
Для этого нам надо сначала слить списки корней в единый связный список, отсортированный по степеням в монотонно возрастающем порядке. Свойство пирамиды обеспечивает нам в новом списке наличие не более двух деревьев одинаковой степени. Далее мы за один проход по этому списку объединим некоторые деревья так, что в результате все они будут иметь попарно разные степени. На каждом шаге нам надо расмотреть несколько случаев.
- Рассматриваемое дерево и следующее за ним имеют разные степени (случай a на рисунке). Ситуация тривиальна и не требует никаких действий. Переходим к следующему шагу.
- Текущее дерево и его два ближаших соседа справа (то есть те, которые встретятся на последующих итерациях) имеют одинаковые степени (случай b на рисунке). Эта ситуация хоть и не тривиальна, но ее следует оставить для следующего шага.
- Если степень текущего и последующего деревьев одинакова (случай c-d на рисунке), то нам следует объединить их в новое дерево (сделав корнем вершину того дерева, чей ключ наименьший), степень которого будет на единицу больше той, что была ранее.
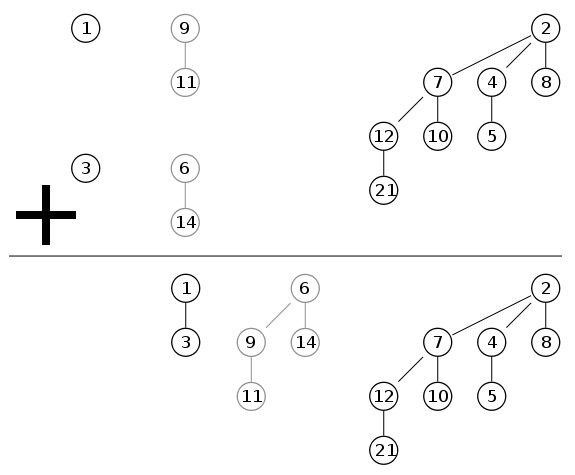
Пример пирамиды до merge и после:
insert
Необходимо просто создать биномиальную пирамиду с одним узлом за время и объединяет ее с биномиальной пирамидой Н, содержащей n узлов, за время .
extractMin
Приведенная ниже процедура извлекает узел с минимальным ключом из биномиальной кучи и возвращает указатель на извлеченный узел:
Node extractMin(H) {
//поиск корня х с минимальным значением ключа в списке корней Н, и удаление х из корней Н
min = ;
x = null;
curx = head[H];
while curx null {
if curx.key < min {
min = curx.key;
x = curx;
}
curx = curx.next;
}
x.prev.next = x.next;
x.next.prev = x.prev;
//добавление детей элемента x в кучу.
H' = makeBinomialHeap();
curx = x.child;
while curx null {
p[curx] = null;
head[H'] = curx;
H = merge(H, H');
curx = curx.sibling;
}
return x;
}
Поскольку минимальный элемент находится в корневом списке, найти его легко; после его удаления соответствующее дерево рассыпается в набор биномиальных деревьев меньшего размера, который надо объединить с оставшейся частью кучи. Все действия выполняются за время , так что общее время работы процедуры есть .
decreaseKey
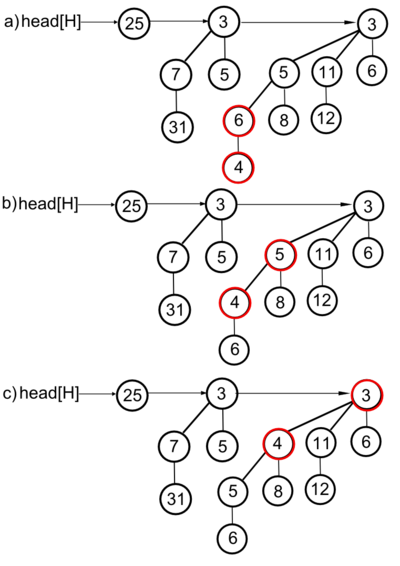
Следующая процедура уменьшает ключ элемента x биномиальной кучи, присваивая ему новое значение. Вершина, ключ которой был уменьшен, «всплывает» наверх. Процедура выполняется за время , поскольку глубина вершины x есть (свойства биномиального дерева), а при выполнении каждого шага алгоритма мы поднимаемся вверх.
void decreaseKey(H, x, k) {
if k > key[x] then
return;
key[x] = k;
y = x;
z = p[y];
while z null and key[y] < key[z] do {
swap(key[y], key[z]);
y = z;
z = p[y];
}
}
Пример работы процедуры проиллюстрирован на рисунке (y - уменьшаемый элемент, z - его предок).
delete
Удаление ключа сводится к двум предыдущим операциям: мы уменьшаем ключ до минимально возможного значения, а затем удаляем вершину с минимальным ключом. В процессе выполнения процедуры это значение всплывает вверх, откуда и удаляется. Процедура выполняется за время .
void delete(H, x) {
decreaseKey(H, x, -);
extractMin(H);
}
Источники
- Биномиальные кучи — INTUIT.ru
- Binomial heap — Wikipedia
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 538-558. — ISBN 5-8489-0857-4