Фибоначчиева куча — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Фибоначчиевы кучи)
(→‎Фибоначчиевы кучи)
Строка 99: Строка 99:
  
 
Поскольку <tex>\left\vert (-\varphi)^{-1} \right\vert < 1</tex>, то выполняются неравенства <tex dpi="160">\frac {(-\varphi)^{-n}} {\sqrt 5} < \frac {1} {\sqrt 5} < \frac {1} {2}</tex>. Таким образом, <tex>n</tex>-е число Фибоначчи равно <tex dpi="160">\frac {\varphi^{n}} {\sqrt 5}</tex>, округленному до ближайшего целого числа. Следовательно, <tex>F_n =\Theta(\varphi^n)</tex>.
 
Поскольку <tex>\left\vert (-\varphi)^{-1} \right\vert < 1</tex>, то выполняются неравенства <tex dpi="160">\frac {(-\varphi)^{-n}} {\sqrt 5} < \frac {1} {\sqrt 5} < \frac {1} {2}</tex>. Таким образом, <tex>n</tex>-е число Фибоначчи равно <tex dpi="160">\frac {\varphi^{n}} {\sqrt 5}</tex>, округленному до ближайшего целого числа. Следовательно, <tex>F_n =\Theta(\varphi^n)</tex>.
 +
}}
 +
 +
 +
{{Лемма
 +
|id=лемма4
 +
|statement=Максимальная степень <tex>D(n)</tex> произвольной вершины в фибоначчиевой куче с <tex>n</tex> вершинами равна <tex>O(log(n))</tex>
 +
|proof=
 +
Пусть <tex>x</tex> {{---}} произвольная вершина в фибоначчиевой куче с <tex>n</tex> вершинами, и пусть <tex>k</tex> {{---}} степень вершины <tex>x</tex>. Тогда по [[#лемма2|доказанному выше]] в дереве, корень которого <tex>x</tex>, содержится не менее <tex>F_k</tex> вершин, что в свою очередь по [[#Лемма3|лемме]] не менее <tex>\varphi^{k}</tex>.
 +
То есть
 +
 +
<tex>n \geqslant \varphi^{k}</tex>
 +
 +
Логарифмируя по основанию <tex>\varphi</tex>, получаем
 +
 +
<tex>log_{\varphi}n \geqslant k</tex>
 +
 +
Таким образом, максимальная степень вершины <tex>D(n)</tex> равна <tex>O(log(n))</tex>.
 
}}
 
}}
  

Версия 22:22, 8 марта 2012

Фибоначчиевы деревья

Определение:
Фибоначчиево дерево - биномиальное дерево, где у каждой вершины удалено не более одного ребенка.


Определение:
Фибоначчиево дерево порядка [math]n[/math] - биномиальное дерево порядка [math]n[/math], из которого оно получено.


Лемма:
Для всех целых [math] n \geqslant 2[/math]

[math] F_n = 1 + \sum\limits_{i=0}^{n-2} F_i [/math], где [math] F_n [/math] — [math] n [/math] число Фибоначчи, определяемое формулой:

[math] F_n = \begin{cases} 0, & n = 0 \\ 1, & n = 1 \\ F_{n-1} + F_{n-2}, & n \geqslant 2 \end{cases} [/math]
Доказательство:
[math]\triangleright[/math]

Докажем лемму по индукции:

при [math]n = 2[/math]

[math]F_2 = 1 + \sum\limits_{i=0}^0 F_i = 1 + 0 = 1[/math], что действительно верно.

По индукции предполагаем, что [math]F_{n-1} = 1 + \sum\limits_{i=0}^{n-3} F_i [/math]. Тогда

[math]F_n = F_{n-1} + F_{n-2} = 1 + \sum\limits_{i=0}^{n-3} F_i + F_{n-2} = 1 + \sum\limits_{i=0}^{n-2} F_i[/math]
[math]\triangleleft[/math]
Лемма:
Фибоначчиево дерево порядка [math]n[/math] содержит не менее [math]F_n[/math] вершин.
Доказательство:
[math]\triangleright[/math]

Докажем это утверждение по индукции. Пусть [math]s_n[/math] — минимальный размер фибоначчиева дерева порядка n.

При [math]n = 0[/math]

[math]s_0 = 1 \gt F_0[/math].

При [math]n = 1[/math]

[math]s_1 = 1 = F_1[/math].

Предположим по индукции, что для всех [math]i \lt n \ s_i \geqslant F_i[/math]. Пусть в нашем дереве удалено поддерево порядка [math]n - 1[/math]. Тогда

[math]s_n = 1 + \sum\limits_{i=0}^{n-2} s_i \geqslant 1 + \sum\limits_{i=0}^{n-2} F_i[/math]

Но по предыдущей лемме [math]1 + \sum\limits_{i=0}^{n-2} F_i = F_n[/math]. Следовательно, [math]s_n \geqslant F_n[/math]
[math]\triangleleft[/math]

Фибоначчиевы кучи

Определение:
Фибоначчиева куча - набор фибоначчиевых деревьев, упорядоченных в соответствии со свойством неубывающей кучи.


Пример фибоначчиевой кучи

Фибоначчиевы кучи поддерживают тот же набор операций, что и биномиальные кучи, но имеют то преимущество, что операции, в которых не требуется удаление, имеют амортизированное время работы, равное [math]O(1)[/math].

С теоретической точки зрения фибоначчиевы кучи особенно полезны в случае, когда количество операций [math]ExtractMin[/math] и [math]Delete[/math] относительно мало по сравнению с количеством других операций. Однако с практической точки зрения программная сложность и высокие значения постоянных множителей в формулах времени работы существенно снижают эффективность применения фибоначчиевых куч, делая их в большинстве случаев менее привлекательными, чем обычные бинарные кучи.


Определение:
Степень вершины - порядок фибоначчиева дерева, чьим корнем эта вершина является.


Лемма:
[math]F_n =\Theta(\varphi^n)[/math], где [math] \varphi = \frac {1 + \sqrt 5} {2}[/math]
Доказательство:
[math]\triangleright[/math]

Для начала докажем, что [math]F_n =[/math] [math]\frac {\varphi^n - (-\varphi)^{-n}} {\sqrt 5}[/math]

Используем для этого математическую индукцию.

При [math]n = 0[/math]

[math]F_0 =[/math] [math]\frac {\varphi^0 - (-\varphi)^0} {\sqrt 5} = \frac {1 - 1} {\sqrt 5} = 0[/math], что верно.

При [math]k = 1[/math]

[math]F_1 =[/math] [math]\frac {\varphi^1 - (-\varphi)^{-1}} {\sqrt 5} = \frac {1} {\sqrt 5}(\frac {1 + \sqrt 5} {2} - \frac {1 - \sqrt 5} {2}) = \frac {2\sqrt 5} {2\sqrt 5} = 1[/math], что также верно.

По индукции предполагаем, что [math]F_{n-1} =[/math] [math]\frac {\varphi^{n-1} - (-\varphi)^{1-n}} {\sqrt 5}[/math] и [math]F_{n-2} =[/math] [math]\frac {\varphi^{n-2} - (-\varphi)^{2-n}} {\sqrt 5}[/math]. Тогда

[math]F_n = F_{n-1} + F_{n-2} =[/math] [math]\frac {\varphi^{n-1} - (-\varphi)^{1-n}} {\sqrt 5} + \frac {\varphi^{n-2} - (-\varphi)^{2-n}} {\sqrt 5} =[/math]

[math]= \frac {1} {\sqrt 5}[/math] [math](\varphi^{n-1} - (-\varphi)^{1-n} + \varphi^{n-2} - (-\varphi)^{2-n}) [/math] [math]= \frac {1} {\sqrt 5}[/math] [math](\varphi^{n}(\varphi^{-1} + \varphi^{-2}) - (-\varphi)^{-n}(-\varphi + \varphi^{2}))[/math]

Подставив вместо [math]\varphi[/math] его значение, нетрудно убедится, что [math]\varphi^{-1} + \varphi^{-2} = -\varphi + \varphi^{2} = 1[/math]

Поскольку [math]\left\vert (-\varphi)^{-1} \right\vert \lt 1[/math], то выполняются неравенства [math]\frac {(-\varphi)^{-n}} {\sqrt 5} \lt \frac {1} {\sqrt 5} \lt \frac {1} {2}[/math]. Таким образом, [math]n[/math]-е число Фибоначчи равно [math]\frac {\varphi^{n}} {\sqrt 5}[/math], округленному до ближайшего целого числа. Следовательно, [math]F_n =\Theta(\varphi^n)[/math].
[math]\triangleleft[/math]


Лемма:
Максимальная степень [math]D(n)[/math] произвольной вершины в фибоначчиевой куче с [math]n[/math] вершинами равна [math]O(log(n))[/math]
Доказательство:
[math]\triangleright[/math]

Пусть [math]x[/math] — произвольная вершина в фибоначчиевой куче с [math]n[/math] вершинами, и пусть [math]k[/math] — степень вершины [math]x[/math]. Тогда по доказанному выше в дереве, корень которого [math]x[/math], содержится не менее [math]F_k[/math] вершин, что в свою очередь по лемме не менее [math]\varphi^{k}[/math]. То есть

[math]n \geqslant \varphi^{k}[/math]

Логарифмируя по основанию [math]\varphi[/math], получаем

[math]log_{\varphi}n \geqslant k[/math]

Таким образом, максимальная степень вершины [math]D(n)[/math] равна [math]O(log(n))[/math].
[math]\triangleleft[/math]

Операции

Потенциал

Введем потенциал фибоначчиевой кучи [math] \Phi(H) = C(t[H] + 2m[H]) [/math], где [math] t[H] [/math] — количество элементов в корневом списке кучи, а [math] m[H] [/math] — количество вершин, у которых удален один ребенок (то есть вершин с пометкой [math] mark[x] == true [/math]). Подходящую константу [math] C [/math] выберем позже, на этапе анализа каскадного вырезания. На языке метода предоплаты это выглядит следующим образом: возле каждого корня лежит одна монета, а возле каждой вершины, у которой удалили ребенка, лежит две монеты.

Создание кучи

Создается новый пустой корневой список, в [math] min[H] [/math] устанавливается значение [math] null [/math]. Реальное время работы — [math] O(1) [/math].

Слияние

Слияние двух фибоначчиевых куч происходит просто: объединяем списки этих куч в один, релаксируем минимум. Реальное время работы — [math] O(1) [/math]. Амортизированное время работы - также [math] O(1) [/math], поскольку, при объединении двух куч в одну, потенциалы обеих куч суммируются, итоговая сумма потенциалов не изменяется, [math] \Phi_{n + 1} - \Phi_n = 0 [/math].

Вставка элемента

Вставка элемента в фибоначчиеву кучу также тривиальна: создается новая куча из одного элемента и сливается с текущей. Амортизированная стоимость операции: 1 (создание кучи) + 2 (слияние куч + релаксация минимума) + 1(изменение потенциала) = 4.

Извлечение минимума

Первая рассматриваемая операция, в ходе которой меняется структура кучи. Здесь используется вспомогательная процедура Consolidate ("уплотнение" кучи). Возьмем указатель на [math] min[H] [/math], удалим эту вершину. Ее поддеревья (их не более, чем [math] D[H] [/math], где [math] D[H] [/math] — максимальная степень вершины в куче) все положим в корневой список. Теперь вызываем процедуру [math] Consolidate [/math].

"Уплотнение" (Consolidate)

Данная процедура принимает кучу, и делает из нее кучу, в корневом списке которой [math] O(D[H]) [/math] вершин.

Для этого возьмем массив списков указателей на корни деревьев [math] A[0..D[H]] [/math], где [math] D[H] [/math] — максимальная степень вершины в текущем корневом списке. Далее мы увидим, что [math] D[H] = O(logN) [/math].

Затем происходит процесс, аналогичный слиянию биномиальных куч : добавляем поочередно каждый корень, смотря на его степень. Пусть она равна [math] d [/math]. Если в соответствующей ячейке A еще нету вершины, записываем текущую вершину туда. Иначе подвешиваем одно дерево к другому, и пытаемся также добавить дерево, степень корня которого уже равна [math] d + 1 [/math]. Продолжаем, пока не найдем свободную ячейку.

Учетная стоимость [math] Consolidate [/math] равна [math] O(D[H]) [/math]. Докажем это:

Пусть изначально в корневом списке было [math] r [/math] вершин. Тогда в ходе операции [math] Consolidate [/math] мы сделали [math] O(r) [/math] слияний деревьев. Но эти [math] O(r) [/math] слияний скомпенсируются уменьшением потенциала [math] t_i + \Phi_i - \Phi_{i - 1} = r + C(O(D[H]) - r) = O(D[H]) [/math]. Остальных действий будет также [math] O(D[H]) [/math]. Таким образом, учетная стоимость [math] Consolidate: \, O(D[H]) [/math].

На языке метода предоплаты: Положим у каждой вершины-ребенка удаленной монету. Это [math] O(D[H]) [/math] действий. Теперь: у каждой вершины в корневом списке лежит монета, потратим ее на то, чтобы провести процедуру [math] Consolidate [/math]. Получили новый корневой список, снова раздаем монеты каждой вершине. Итого [math] O(D[H]) + O(D[H]) = O(D[H]) [/math] действий.

Уменьшение ключа

Основная идея: хотим, чтобы учетная стоимость данной операции была [math] O(1) [/math]. Было бы хорошо, чтобы вершина не всплывала до корня; тогда дерево не придется сильно перестраивать. Для этого, при удобном случае будем вырезать поддерево полностью и перемещать его в корневой список. Итак, сам алгоритм:

  1. Проверяем, если новое значение ключа все же не меньше значения ключа родителя, то все хорошо, и мы выходим.
  2. Иначе, вырезаем дерево с текущей вершиной в корневой список, и производим каскадное вырезание родителя.

Вырезание вершины

При вырезании вершины мы удаляем ее из списка детей своего родителя, уменьшаем степень ее родителя ([math] degree[p[x]] [/math]) и снимаем пометку с текущей вершины ([math] mark[x] = false [/math]).

Каскадное вырезание

Каскадное вырезание

Перед вызовом каскадного вырезания нам известно, что перед этим мы удалили ребенка у этой вершины. Если [math] mark[x] == false [/math], то мы ставим эту пометку [math] true [/math] и заканчиваем. В противном случае, вырезаем текущую вершину, и запускаем каскадное вырезание от родителя.

Докажем, что амортизированное время работы операции "уменьшение ключа" есть [math] O(1) [/math]. Поскольку в процедуре нет циклов, ее время работы определяется лишь количеством рекурсивных вызовов каскадного вырезания.

Пусть мы вызвали процедуру каскадного вырезания [math] k [/math] раз. Тогда вершин с пометкой [math] mark[x] == true [/math] стало на [math] k [/math] меньше, а в корневом списке прибавилось [math] k [/math] новых вершин. Итого, время работы будет: [math] O(k) + \Phi_i - \Phi_{i - 1} = O(k) + C(k - 2k + O(1)) [/math]. Теперь, подбирая соответствующую константу в потенциале, можем добиться того, чтобы амортизированное время работы этой процедуры стало [math] O(1) [/math]. Теперь также стало ясно, для чего в определении нашего потенциала количество вершин с пометкой [math] mark[x] [/math] учитывается вдвое больше, чем количество вершин в корневом списке.

На языке метода предоплаты: Покажем, что взяв в начале 4 монеты, нам хватит этого для выполнения данной операции. Возьмем 4 монеты перед началом уменьшения ключа. Теперь 1 монету потратим на перенос в корневой список и релаксацию минимума, еще 1 - на то, чтобы положить монету у новой вершины в корневом списке. У нас осталось 2 монеты. Далее производим каскадное вырезание: в случае, когда [math] mark[p[x]] == false [/math], кладем 2 монеты к этой вершине, и устанавливаем соответствующую пометку. Инвариант сохраняется.

Иначе, [math] mark[p[x]] == true [/math] и там лежит 2 монеты. 2 + 2 = 4, и мы можем рекурсивно продолжить данный процесс. Оценка доказана.

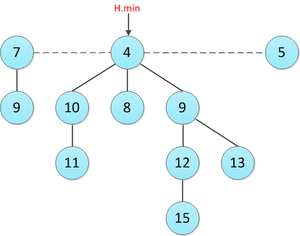
На рисунке проиллюстрирован процесс понижения ключа вершины c 10 до 7. Серым помечены вершины с [math] mark[x] == true [/math].

Удаление вершины

Удаление вершины реализуется через уменьшение ее ключа до [math] -\infty [/math] и последующим извлечением минимума. Амортизированное время работы: [math] O(1) + O(D[H]) = O(D[H]) [/math].

Поскольку, ранее мы показали, что [math] D[H] = O(log|H|) = O(logN) [/math], то соответствующие оценки доказаны.

Ссылки

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Фибоначчиева_куча&oldid=18985»