СНМ (наивные реализации) — различия между версиями
Free0u (обсуждение | вклад) м (→Источники) |
Free0u (обсуждение | вклад) (→С помощью списка) |
||
| Строка 65: | Строка 65: | ||
s[i].tail = s[i] | s[i].tail = s[i] | ||
| − | find(x)://подразумевается, что x - ссылка на один из элементов | + | find(x): //подразумевается, что x - ссылка на один из элементов |
while x.next != Null: | while x.next != Null: | ||
| − | x = x. | + | x = x.next |
return x.set | return x.set | ||
| − | union(x, y)://здесь важно, что x и y - представители множеств | + | union(x, y): //здесь важно, что x и y - представители множеств |
if x == y: | if x == y: | ||
return | return | ||
| Строка 78: | Строка 78: | ||
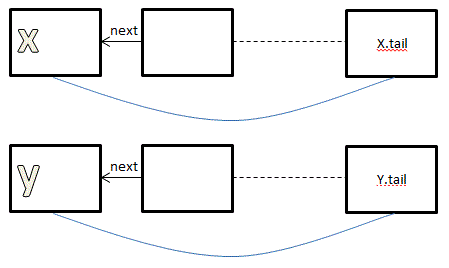
Два списка до операции union: | Два списка до операции union: | ||
| + | |||
[[Файл:1.GIF]] | [[Файл:1.GIF]] | ||
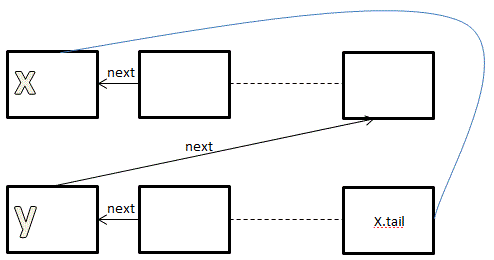
Два списка после операции union: | Два списка после операции union: | ||
| + | |||
[[Файл:2.GIF]] | [[Файл:2.GIF]] | ||
Версия 23:19, 13 марта 2012
| Определение: |
| Система непересекающихся множеств(disjoint set union, DSU) - структура данных, поддерживающая операции - объединения множеств, содержащих x и y, и - поиск множества, которому принадлежит элемент k. |
Содержание
Пример работы
Здесь будет пример работы
Реализации
С помощью массива "цветов"
Оценка работы:
Введем массив , в будет храниться цвет множества, к которому принадлежит . Тогда , очевидно, будет работать за .
Чтобы объединить множества и , надо изменить все , равные цвету , на цвет . Тогда работает за .
Псевдокод:
int color[n]
init():
for i = 0 to n - 1:
color[i] = i //сначала каждый элемент лежит в своем множестве
find(k):
return color[k]
union(x, y):
if color[x] == color[y]:
return
else:
t = color[y]
for i = 0 to n - 1:
if color[i] == t:
color[i] = color[x]
С помощью списка
Оценка работы
Пусть каждое множество хранится в виде списка. Вначале создается n списков, в котором каждый элемент является представителем своего множества. Для каждого списка будем хранить ссылку на следующий элемент(next) и ссылку на хвост(tail). Тогда для объединения множеств надо будет просто перекинуть ссылку next на начало другого множества. Таким образом, работает за .
Для того, чтобы найти элемент в одном из множеств, надо идти по next'ам, пока он не указывает на Null - тогда мы нашли элемент-представитель. Таким образом, работает за .
Псевдокод:
s[n]
init():
for i = 0 to n - 1:
s[i].set = i
s[i].next = Null
s[i].tail = s[i]
find(x): //подразумевается, что x - ссылка на один из элементов
while x.next != Null:
x = x.next
return x.set
union(x, y): //здесь важно, что x и y - представители множеств
if x == y:
return
else:
y.next = x.tail
x.tail = y.tail
Два списка до операции union:
Два списка после операции union:
Другие реализации
Источники
- Т. Кормен - Алгоритмы, построение и анализ. Второе издание. Часть V. Глава 21.