Предикат "левый поворот"

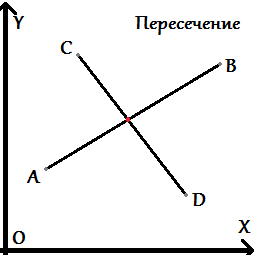
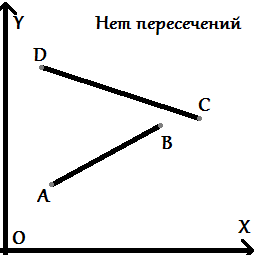
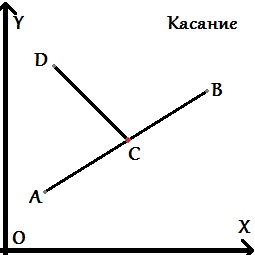
Даны два отрезка, которые задаются начальной и конечной точками [math]a,b\ \mathcal{2}\ \mathbb R^2[/math] и определяются как множества точек [math]s\ =\ \{(1-t)a + tb,\ t\ \in [0;1]\}[/math]. Требуется проверить существование множества их общих точек. Для определения этого факта в вычислительной геометрии используется предикат левый поворот (или по часовой стрелке). Рассмотрим возможные расположения точек и самих отрезков относительно друг друга:

Определим, лежат ли точки концов отрезков по разные стороны от другого отрезка.

Определение:

[math] $$ \operatorname{LeftTurn}(a, b, c) =\left\{ \begin{array}{rl} -1 &\mbox{, if}\ (b - a)\times(c - a) \lt 0\\ 0 &\mbox{, if}\ (b - a)\times(c - a) = 0\\ 1 &\mbox{, if}\ (b - a)\times(c - a) \gt 0 \end{array} \right. $$ [/math]

Распишем подробнее: [math](b - a)\times(c - a) = (b_x - a_x)(c_y - a_y) - (b_y - a_y)(c_x - a_x) = A - B[/math]

Какие при этом у нас будут погрешности? Допустим, что все числа положительные и будем писать без модулей:

Замечание: при сложении складываются абсолютные погрешности, при умножении складываются относительные погрешности.

[math] \delta (b - a)\times(c - a) = A \varepsilon \left(\frac{(b_x + a_x)}{(b_x \cdot a_x)} + \frac{(c_y + a_y)}{(c_y \cdot a_y)}\right) + B \varepsilon \left(\frac{(b_y + a_y)}{(b_y \cdot a_y)} + \frac{(c_x + a_x)}{(c_x \cdot a_x)}\right)[/math]

Заметим, что все координаты (а, значит, и наши вычисления) производятся в вещественных числах, а это значит, что при вычислениях мы можем допустить ошибку. Более точно, определить знак нашего выражения поможет вычисление с интервальной арифметикой. Все исходные переменные будут вырожденными интервалами. Из-за погрешностей, возникающих при округлении вещественных чисел, истинные значения операций нам будут неизвестны, но они обязательно будет содержаться в посчитанных интервалах. Для точного вычисления необходимо фильтрованное вычисление предикатов.

[math]\overbrace {(b - a)\times(c - a)}^{v} \approx \overbrace{(b_x \ominus a_x)\otimes(c_y \ominus a_y) \ominus (b_y \ominus a_y)\otimes(c_x \ominus a_x)}^{\tilde{v}} =[/math]

[math]= \big((b_x - a_x)(c_y - a_y)(1 + \delta_1)(1 + \delta_2)(1 + \delta_3)\ -[/math]

[math]-\ (b_y - a_y)(c_x - a_x)(1 + \delta_4)(1 + \delta_5)(1 + \delta_6)\big)(1 + \delta_7)[/math]

[math]\mid\delta_i\mid \le \varepsilon[/math];

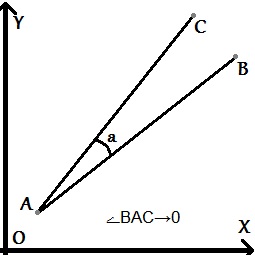
Именно поэтому, когда угол между отрезками АВ и АС крайне мал, мы можем получить неверное значение предиката.

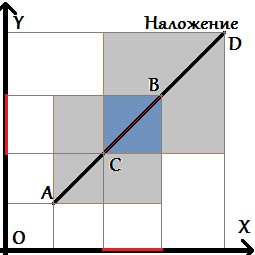
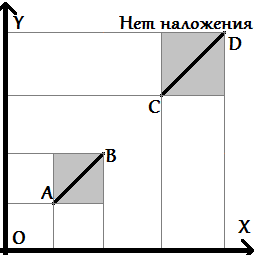
Bounding box

Ещё следует обратить внимание на граничные случаи, когда какие-то точки попадают на саму прямую. При этом возникает единственный особый случай, когда вышеописанные проверки ничего не дадут — случай, когда оба отрезка лежат на одной прямой. Этот случай надо рассмотреть отдельно. Для этого достаточно проверить, что проекции этих двух отрезков на оси X и Y пересекаются (часто эту проверку называют проверкой на bounding box).

План решения

Итак, теперь зная, какие подводные камни нам могут встретиться, накидаем план вычисления предиката:

рас-рас, тут еще пишу