Декартово дерево

Эта статья про Курево

Декартово дерево — это структура данных, объединяющая в себе бинарное дерево поиска и бинарную кучу (отсюда и второе её название: treap (tree + heap) и дерамида (дерево + пирамида), так же существует название курево (куча + дерево).

Более строго, это бинарное дерево, в узлах которого хранится пары [math] (x,y) [/math], где [math]x[/math] - это ключ, а [math]y[/math] - это приоритет. Также оно является двоичным деревом поиска по [math]x[/math] и пирамидой по [math]y[/math]. Предполагая, что все [math]x[/math] и все [math]y[/math] являются различными, получаем, что если некоторый элемент дерева содержит [math](x_0,y_0)[/math], то у всех элементов в левом поддереве [math]x \lt x_0[/math], у всех элементов в правом поддереве [math] x \gt x_0[/math], а также и в левом, и в правом поддереве имеем: [math] y \lt y_0[/math].

Дерамиды были предложены Сиделем (Siedel) и Арагоном (Aragon) в 1996 г.

Операции в декартовом дереве

Split

Операция split

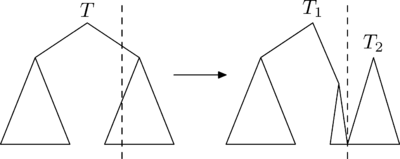
Операция [math]\mathrm{Split}[/math] (разрезать) позволяет сделать следующее: разрезать декартово дерево [math]T[/math] по ключу [math]k[/math] и получить два других декартовых дерева: [math]T_1[/math] и [math]T_2[/math], причем в [math]T_1[/math] находятся все ключи дерева [math]T[/math], не большие [math]k[/math], а в [math]T_2[/math] — большие [math]k[/math].

[math]\mathrm{Split}(T, k) \to \{T_1, T_2\}[/math].

Эта операция устроена следующим образом.

Рассмотрим случай, в котором требуется разрезать дерево по ключу, большему ключа корня. Посмотрим, как будут устроены результирующие деревья [math]T_1[/math] и [math]T_2[/math]:

• [math]T_1[/math]: левое поддерево [math]T_1[/math] совпадёт с левым поддеревом [math]T[/math]. Для нахождения правого поддерева [math]T_1[/math], нужно разрезать правое поддерево [math]T[/math] на [math]T^R_1[/math] и [math]T^R_2[/math] по ключу [math]k[/math] и взять [math]T^R_1[/math].
• [math]T_2[/math] совпадёт с [math]T^R_2[/math].

Случай, в котором требуется разрезать дерево по ключу, меньше либо равному ключа в корне, рассматривается симметрично.

Псевдокод:

Treap T // декартово дерево
Node k // ключ по которому нужно разрезать декартово дерево

Split (Treap T, Node k, Treap T1, Treap T2) { // T1, T2 - результат процедуры Split
  if (T == NULL) {
    T1 = T2 = NULL
  }
  else if (k.x > T.x) {
    Split (T.right, k, T.right, T2)
    T1 = T
  }
  else {
    Split (T.left, k, T1, T.left)
    T2 = T
  }
}

Оценим время работы операции [math]\mathrm{Split}[/math]. Во время выполнения вызывается одна операция [math]\mathrm{Split}[/math] для дерева хотя бы на один меньшей высоты и делается ещё [math]\mathcal{O}(1)[/math] операция. Тогда итоговая трудоёмкость этой операции равна [math]\mathcal{O}(h)[/math], где [math]h[/math] — высота дерева.

Merge

Операция merge

Рассмотрим вторую операцию с декартовыми деревьями — [math]\mathrm{Merge}[/math](слить).

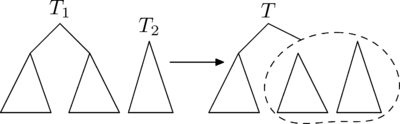
С помощью этой операции можно слить два декартовых дерева в одно. Причем, все ключи в первом(левом) дереве должны быть меньше, чем ключи во втором(правом). В результате получается дерево, в котором есть все ключи из первого и второго деревьев.

[math]\mathrm{Merge}(T_1, T_2) \to T[/math]

Рассмотрим принцип работы этой операции. Пусть нужно слить деревья [math]T_1[/math] и [math]T_2[/math]. Тогда, очевидно, у результирующего дерева [math]T[/math] есть корень. Корнем станет вершина из [math]T_1[/math] или [math]T_2[/math] с наибольшим ключом [math]y[/math]. Но вершина с самым большим [math]y[/math] из всех вершин деревьев [math]T_1[/math] и [math]T_2[/math] может быть только либо корнем [math]T_1[/math], либо корнем [math]T_2[/math]. Рассмотрим случай, в котором корень [math]T_1[/math] имеет больший [math]y[/math], чем корень [math]T_2[/math]. Случай, в котором корень [math]T_2[/math] имеет больший [math]y[/math], чем корень [math]T_1[/math], симметричен этому.

Если [math]y[/math] корня [math]T_1[/math] больше [math]y[/math] корня [math]T_2[/math], то он и будет являться корнем. Тогда левое поддерево [math]T[/math] совпадёт с левым поддеревом [math]T_1[/math]. Справа же нужно подвесить объединение правого поддерева [math]T_1[/math] и дерева [math]T_2[/math].

Псевдокод:

Treap T // результат процедуры Merge
Treap T1, T2 // сливаемые деревья

Merge (Treap T, Treap T1, Treap T2) {
  if (T1 == NULL || T2 == NULL) {
    if (T1 != NULL) {
      T = T1
    }
    else {
      T = T2
    }
  }
  else if (T1.y > T2.y) {
    Merge (T1.right, T1.right, T2)
    T = T1
  }
  else {
    Merge (T2.left, T1, T2.left)
    T = T2
  }
}

Рассуждая аналогично операции [math]\mathrm{Split}[/math] приходим к выводу, что трудоёмкость операции [math]\mathrm{Merge}[/math] равна [math]\mathcal{O}(h)[/math], где [math]h[/math] — высота дерева.

Insert

Операция [math]\mathrm{Insert}(T, k)[/math] добавляет в дерево [math]T[/math] элемент [math]k[/math], где [math]k.x[/math] — ключ, а [math]k.y[/math]— приоритет.

• Реализация №1

1. Разобьём наше дерево по ключу, который мы хотим добавить, то есть [math]\mathrm{Split}(T, k.x) \to \{T_1, T_2\}[/math].
2. Сливаем первое дерево с новым элементом, то есть [math]\mathrm{Merge}(T_1, k) \to T_1[/math].
3. Сливаем получившиеся дерево со вторым, то есть [math]\mathrm{Merge}(T_1, T_2) \to T[/math].

• Реализация №2

1. Сначала спускаемся по дереву (как в обычном бинарном дереве поиска по [math]k.x[/math]), но останавливаемся на первом элементе, в котором значение приоритета оказалось меньше [math]k.y[/math].
2. Теперь вызываем [math]\mathrm{Split }(T, k.x) \to \{T_1, T_2\}[/math] от найденного элемента (от элемента вместе со всем его поддеревом)
3. Полученные [math]T_1[/math] и [math]T_2[/math] записываем в качестве левого и правого сына добавляемого элемента.
4. Полученное дерево ставим на место элемента, найденного в первом пункте.

Remove

Операция [math]\mathrm{Remove}(T, x)[/math] удаляет из дерева [math]T[/math] элемент с ключом [math]x[/math].

• Реализация №1

1. Разобьём наше дерево по ключу, который мы хотим удалить, то есть [math]\mathrm{Split }(T, k.x) \to \{T_1, T_2\}[/math].
2. Теперь отделяем от первого дерева элемент [math]x[/math], опять таки разбивая по ключу [math]x[/math], то есть [math]\mathrm{Split }(T_1, k.x - \varepsilon) \to \{T_1, T_3\}[/math].
3. Сливаем первое дерево со вторым, то есть [math]\mathrm{Merge }(T_1, T_2) \to T[/math].

• Реализация №2

1. Спускаемся по дереву (как в обычном бинарном дереве поиска по [math]x[/math]), ища удаляемый элемент.
2. Найдя элемент, вызываем [math]Merge[/math] его левого и правого сыновей
3. Возвращаемое значение функции [math]Merge[/math] ставим на место удаляемого элемента.

Случайные ключи

Мы уже выяснили, что сложность операций с декартовым деревом линейно зависит от его высоты. В действительности высота декартова дерева может быть линейной относительно его размеров. Например, высота декартова дерева, построенного по набору ключей [math](1, 1), \ldots, (n, n)[/math], будет равна [math]n[/math]. Во избежание таких случаев, полезным оказывается выбирать приоритеты в ключах случайно.

Высота в декартовом дереве

Теорема:

Декартово дерево из [math]n[/math] узлов, ключи [math]y[/math] которых являются независимыми случайными величинами одного и того же распределения, имеет высоту [math]O(\log n)[/math].

Доказательство:

[math]\triangleright[/math]

Для начала введем несколько обозначений: [math]x_k[/math] — вершина с [math]k[/math]-ым по величине ключом; индикаторная величина [math]A_{i, j} = \left\{\begin{array}{lllc} 1 &&, x_i\ \text{is ancestor of} \ x_j\\ 0 &&, \text{otherwise}\\ \end{array}\right. [/math] [math]d(v)[/math] - глубина вершины [math]v[/math]; В силу обозначений глубину вершины можно записать как количество предков: [math]d(x_k) = \sum\limits_{i = 1}^{n} A_{i,k} [/math]. Теперь можно выразить математическое ожидание глубины конкретной вершины: [math]E(d(x_k)) = \sum\limits_{i = 1}^{n} Pr[A_{i,k} = 1] [/math] — здесь мы использовали линейность математического ожидания, и то что [math]E(X) = Pr[X = 1][/math] для индикаторной величины [math]X[/math] ([math]Pr[A][/math] — вероятность события [math]A[/math]). Для подсчёта средней глубины вершин нам нужно сосчитать вероятность того, что вершина [math]x_i[/math] является предком вершины [math]x_k[/math], то есть [math]Pr[A_{i,k} = 1][/math]. Введем новое обозначение: [math]X_{i, k}[/math] — множество ключей [math]\{x_i, \ldots, x_k\}[/math] или [math]\{x_k, \ldots, x_i\}[/math], в зависимости от [math]i \lt k[/math] или [math]i \gt k[/math]. [math]X_{i, k}[/math] и [math]X_{k, i}[/math] обозначают одно и тоже, их мощность равна [math]|k - i| + 1[/math]. Лемма: Для любых [math]i \ne k[/math] , [math]x_i[/math] является предком [math]x_k[/math] тогда и только тогда, когда [math]x_i[/math] имеет наименьший приоритет среди [math]X_{i, k}[/math]. Доказательство: [math]\triangleright[/math] Если [math]x_i[/math] является корнем, то оно является предком [math]x_k[/math] и по определению имеет минимальный приоритет среди всех вершин, следовательно, и среди [math]X_{i, k}[/math]. С другой стороны, если [math]x_k[/math] — корень, то [math]x_i[/math] — не предок [math]x_k[/math], и [math]x_k[/math] имеет минимальный приоритет в декартовом дереве; следовательно, [math]x_i[/math] не имеет наименьший приоритет среди [math]X_{i, k}[/math]. Теперь предположим, что какая-то другая вершина [math]x_m[/math] – корень. Тогда, если [math]x_i[/math] и [math]x_k[/math] лежат в разных поддеревьях, то [math]i \lt m \lt k[/math] или [math]i \gt m \gt k[/math], следовательно, [math]x_m[/math] содержится в [math]X_{i , k}[/math]. В этом случае [math]x_i[/math] – не предок [math]x_k[/math], и наименьший приоритет среди [math]X_{i, k}[/math] имеет вершина с номером [math]m[/math]. Наконец, если [math]x_i[/math] и [math]x_k[/math] лежат в одном поддереве, то доказательство применяется по индукции: пустое декартово дерево есть тривиальная база, а рассматриваемое поддерево является меньшим декартовым деревом. [math]\triangleleft[/math] Так как каждая вершина среди [math]X_{i, k}[/math] может иметь минимальный приоритет, мы немедленно приходим к следующему равенству: [math]Pr[A_{i, j} = 1] = \left\{\begin{array}{lllc} \frac{1}{k - i + 1} &&, k \ \gt \ i\\ 0 &&, k\ =\ i\\ \frac{1}{i - k + 1} &&, k \ \lt \ i\\ \end{array}\right. [/math] Подставив последнее в нашу формулу с математическим ожиданием получим: [math]E(d(x_k)) = \sum\limits_{i = 1}^{n} Pr[A_{i,k} = 1] = \sum\limits_{i = 1}^{k - 1} \frac{1}{k - i + 1} + \sum\limits_{i = k + 1}^{n} \frac{1}{i - k + 1} \le ln(k) + ln(n-k)[/math] В итоге мы получили что [math]E(d(x_k)) = O(ln(n))[/math].

[math]\triangleleft[/math]

Ссылки

• Декартово дерево — Википедия
• Treaps и T-Treaps