Двойственный граф планарного графа — различия между версиями
VVolochay (обсуждение | вклад) |
VVolochay (обсуждение | вклад) |
||
| Строка 14: | Строка 14: | ||
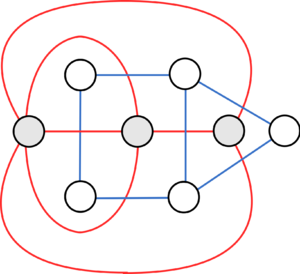
| − | [[Файл: | + | [[Файл:Dual graphs.png|300px|thumb|left|В верхнем двойственном графе есть вершина степени 6, а в нижнем — нет. Следовательно, они не изоморфны.]] |
== Свойства == | == Свойства == | ||
[[Файл:Treenflower new.png|250px|thumb|right|Дерево и двойственный к нему «цветок».]] | [[Файл:Treenflower new.png|250px|thumb|right|Дерево и двойственный к нему «цветок».]] | ||
Версия 12:53, 24 апреля 2012
Определение:
Граф[1] называется двойственным к планарному графу , если:
- Вершины соответствуют граням
- Между двумя вершинами в есть ребро тогда и только тогда, когда соответствующие грани в имеют общее ребро
Чтобы для данного плоского графа построить двойственный , необходимо поместить по вершине в каждую грань (включая внешнюю), а затем, если две грани в имеют общее ребро, соединить ребром соответствующие им вершины в (если грани имеют несколько общих рёбер, соответствующие вершины следует соединить несколькими параллельными рёбрами). В результате всегда получится плоский псевдограф.
Например: тетраэдр — самодвойственный граф, куб и октаэдр — двойственные, так же как додекаэдр и икосаэдр. Эти пять графов, образованные вершинами и рёбрами правильных многогранников, называют платоновыми.
Свойства
- Если — двойственный к двусвязному графу , то — двойственный к
- У одного и того же графа может быть несколько двойственных, в зависимости от конкретной укладки (см. картинку)
- Поскольку любой трёхсвязный планарный граф допускает только одну укладку на сфере[2], у него должен быть единственный двойственный граф
- Мост переходит в петлю, а петля — в мост
- Мультиграф, двойственный к дереву, — цветок
Самодвойственные графы
Определение:
Планарный граф называется самодвойственным, если он изоморфен своему двойственному графу.
Утверждение:
и — самодвойственные графы. Среди полных графов других самодвойственных нет.
Проверить, что и полны и самодвойственны несложно. Докажем, что других нет.
Поскольку грани графа переходят в вершины, количество вершин и граней в исходном графе должно совпадать, т.е. .
Подставив в формулу Эйлера имеем: .
В полном графе .
Получаем квадратное уравнение: .
Его решения: и .
Таким образом, чтобы полный граф был самодвойственным, в нём должна быть ровно одна или четыре вершины.
Поскольку грани графа переходят в вершины, количество вершин и граней в исходном графе должно совпадать, т.е. .
Подставив в формулу Эйлера имеем: .
В полном графе .
Получаем квадратное уравнение: .
Его решения: и .
Таким образом, чтобы полный граф был самодвойственным, в нём должна быть ровно одна или четыре вершины.
Утверждение:
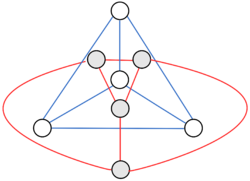
Все колёса самодвойственны.
Это утверждение очевидно.
Достаточно убедиться, что два варианта укладки колеса (вершина с большой степенью внутри или вершина с большой степенью снаружи) двойственны друг другу.
Достаточно убедиться, что два варианта укладки колеса (вершина с большой степенью внутри или вершина с большой степенью снаружи) двойственны друг другу.