Решение RMQ с помощью разреженной таблицы — различия между версиями
(small fix) |
Smolcoder (обсуждение | вклад) (→Применение к задаче RMQ) |
||
| Строка 36: | Строка 36: | ||
== Применение к задаче RMQ == | == Применение к задаче RMQ == | ||
[[Файл:SparseTableRMQ.png|right|Решение задачи RMQ на разреженной таблице]] | [[Файл:SparseTableRMQ.png|right|Решение задачи RMQ на разреженной таблице]] | ||
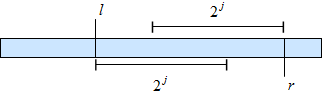
| − | <div>Дан запрос <tex>(l, r)</tex>. По нему найдем <tex>k = \max \{j| 2^j \le r - l + 1\}</tex>, т.е. логарифм длины запрашиваемого отрезка. Заметим, что <tex>k</tex> зависит лишь от длины отрезка. Предпосчитать эту величину за <tex>O(N\log N)</tex> можно введением функции <tex>fl[l] = k</tex>, для которой верно <tex>fl[1] = 0, fl[x] = fl[\lfloor \frac{x}{2}\rfloor] + 1</tex>. | + | <div>Дан запрос <tex>(l, r)</tex>. По нему найдем <tex>k = \max \{j| 2^j \le r - l + 1\}</tex>, т.е. логарифм длины запрашиваемого отрезка. Заметим, что <tex>k</tex> зависит лишь от длины отрезка. |
| − | Далее заметим, что <tex>\min(A[l], A[l+1], ..., A[r]) = \min\left(ST[l][k], ST[r-2^k+1][j]\right)</tex>. Таким образом мы можем находить <tex>k</tex> за <tex>O(1)</tex>.</div> | + | |
| + | Предпосчитать эту величину за <tex>O(N\log N)</tex> можно введением функции <tex>fl[l] = k</tex>, для которой верно <tex>fl[1] = 0, fl[x] = fl[\lfloor \frac{x}{2}\rfloor] + 1</tex>. | ||
| + | Далее заметим, что <tex>\min(A[l], A[l+1], ..., A[r]) = \min\left(ST[l][k], ST[r-2^k+1][j]\right)</tex>. | ||
| + | |||
| + | Таким образом мы можем находить <tex>k</tex> за <tex>O(1)</tex>.</div> | ||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
Версия 22:50, 2 мая 2012
Разреженная таблица (англ. sparse table) позволяет решать задачу online static RMQ за на запрос, с предподсчётом за и использованием памяти.
Содержание
Постановка задачи RMQ
Дан массив действительных чисел. Поступают запросы вида : найти минимум в подмассиве .
Разреженная таблица
Разреженная таблица — двумерная структура данных , для которой выполнено следующее: . Иначе говоря, в этой таблице хранятся минимумы на всех отрезках, длины которых равны степеням двойки. Объём, занимаемый таблицей, равен , и заполненными являются только те элементы, для которых .
Простой метод построения таблицы заключён в следующем реккурентном соотношении:
.
Идемпотентность
Такая простота достигается за счет идемпотентности операции минимум: . Это один из ключевых моментов этого метода, так как она позволяет нам корректно считать минимум в области пересечения отрезков. <wikitex> Пусть $\circ$ — произвольная бинарная операция, которая удовлетворяет свойствам:
- ассоциативности: $a \circ (b \circ c) = (a \circ b) \circ c $;
- коммутативности: $a \circ b = b \circ a$;
- идемпотентности: $a \circ a = a $.
| Утверждение: |
$a_l \circ a_{l+1} \circ \dots \circ a_r = (a_l \circ a_{l+1} \circ \dots \circ a_k) \circ (a_{r - k} \circ a_{r - k + 1} \circ \dots \circ a_r)$, где $l \leqslant k \leqslant r$. |
| Покажем, что $a \circ b \circ c \circ d = (a \circ b \circ c) \circ (b \circ c \circ d)$. Действительно, $a \circ b \circ c \circ b \circ c \circ d = a \circ b \circ b \circ c \circ c \circ d = a \circ b \circ c \circ d $. Будем применять это к выражению в правой части равенства до тех пор, пока не получим выражение в левой части. Поле каждого шага количество одинаковых элементов сократится на два. А так как их конечное четное (по $2k - r$ в каждой скобке) число, то и количество шагов будет конечным. |
Таким образом мы получаем целый класс задач, которые могут решаться разреженной таблицей. </wikitex>
Применение к задаче RMQ
Предпосчитать эту величину за можно введением функции , для которой верно . Далее заметим, что .
Таким образом мы можем находить за .См. также
Источники
- Bender, M.A., Farach-Colton, M. et al. — Lowest common ancestors in trees and directed acyclic graphs. — J. Algorithms 57(2) (2005) — с. 75–94.