Сжатое суффиксное дерево — различия между версиями
м (→Хранение суффиксного дерева) |
|||
| Строка 1: | Строка 1: | ||
| − | [[Суффиксный бор|Суффиксный бор]] {{---}} удобная структура для поиска подстроки в строке, но занимающая много места в памяти. Рассмотрим все такие пути от <tex>u</tex> до <tex>v</tex> в суффиксном боре, в которых каждая вершина имеет только одного сына. | + | [[Суффиксный бор|Суффиксный бор]] {{---}} удобная структура для поиска подстроки в строке, но занимающая много места в памяти. Рассмотрим все такие пути от <tex>u</tex> до <tex>v</tex> в суффиксном боре, в которых каждая вершина имеет только одного сына. Такой путь можно сжать до одного ребра <tex>u v</tex>, пометив его всеми встречающимися на пути символами. Получившееся дерево носит название '''сжатое суффиксное дерево'''. |
==Определение== | ==Определение== | ||
| Строка 6: | Строка 6: | ||
==Защитный символ== | ==Защитный символ== | ||
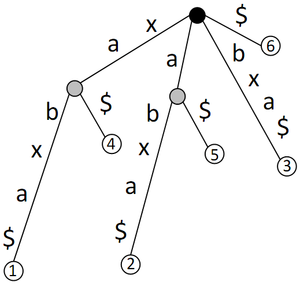
[[Файл:Suffix_tree_3.png|thumb|right|Суффиксное дерево для строки <tex>xabxa</tex> с защитным символом]] | [[Файл:Suffix_tree_3.png|thumb|right|Суффиксное дерево для строки <tex>xabxa</tex> с защитным символом]] | ||
| − | Определение суффиксного дерева не гарантирует, что такое дерево существует для любой строки <tex>s</tex>. Если один суффикс строки совпадает с префиксом другого, то построить суффиксное дерево, удовлетворяющее данному выше определению, невозможно. Например, для строки <tex>xabxa</tex> суффикс <tex>xa</tex> является префиксом суффикса <tex>xabxa.</tex> Во избежание этого в конце строки <tex>s</tex> добавляется символ, не входящий в исходный алфавит. Такой символ называется '''''защитным'''''. Как правило, это <tex>\$</tex>. Любой суффикс строки с защитным символом заканчивается в листе, т.к. он не встречается в строке нигде, кроме позиции последнего символа. | + | Определение суффиксного дерева не гарантирует, что такое дерево существует для любой строки <tex>s</tex>. Если один суффикс строки совпадает с префиксом другого, то построить суффиксное дерево, удовлетворяющее данному выше определению, невозможно. Например, для строки <tex>xabxa</tex> суффикс <tex>xa</tex> является префиксом суффикса <tex>xabxa.</tex> Во избежание этого в конце строки <tex>s</tex> добавляется символ, не входящий в исходный алфавит. Такой символ называется '''''защитным'''''. Как правило, это <tex>\$</tex>. Любой суффикс строки с защитным символом заканчивается в листе и только в листе, т.к. он не встречается в строке нигде, кроме позиции последнего символа. |
Далее <tex>n</tex> - длина строки <tex>s</tex> с защитным символом. | Далее <tex>n</tex> - длина строки <tex>s</tex> с защитным символом. | ||
==Хранение суффиксного дерева== | ==Хранение суффиксного дерева== | ||
| − | Каждое ребро дерева помечается подстрокой исходной строки <tex>s</tex>. Но лучше для него хранить не саму подстроку, а индексы ее начала и конца в исходной строке {{---}} <tex>l, r</tex>. Итак, с каждым ребром дерева ассоциируются две инцидентные ей вершины, символ, с которого начинается подстрока на ребре и два числа <tex>l, r</tex>. Представим дерево как массив <tex>[|V|*|\Sigma|]</tex>, где <tex>|V|</tex> {{---}} количество вершин в дереве, <tex>|\Sigma|</tex> - мощность алфавита. Каждая <tex>[i][j]</tex> ячейка массива содержит информацию о том, в какую вершину ведет <tex>i-</tex>ое ребро по <tex>j-</tex>ому символу и индексы <tex>l, r</tex> подстроки на ребре. | + | Каждое ребро суффиксного дерева помечается подстрокой исходной строки <tex>s</tex>. Но лучше для него хранить не саму подстроку, а индексы ее начала и конца в исходной строке {{---}} <tex>l, r</tex>. Итак, с каждым ребром дерева ассоциируются две инцидентные ей вершины, символ, с которого начинается подстрока на ребре и два числа <tex>l, r</tex>. Представим дерево как массив <tex>[|V|*|\Sigma|]</tex>, где <tex>|V|</tex> {{---}} количество вершин в дереве, <tex>|\Sigma|</tex> - мощность алфавита. Каждая <tex>[i][j]</tex> ячейка массива содержит информацию о том, в какую вершину ведет <tex>i-</tex>ое ребро по <tex>j-</tex>ому символу и индексы <tex>l, r</tex> подстроки на ребре. Очевидно, такое дерево занимает <tex>O(|V||\Sigma|)</tex> памяти. |
==Количество вершин== | ==Количество вершин== | ||
| − | В сжатом суффиксном дереве содержится <tex>n</tex> листьев, т.к. | + | В сжатом суффиксном дереве содержится <tex>n</tex> листьев, т.к. строка <tex>s</tex> содержит ровно <tex>n</tex> суффиксов. Рассмотрим теперь количество внутренних вершин такого дерева. |
{{Лемма | {{Лемма | ||
| Строка 30: | Строка 30: | ||
Рассмотрим все вершины в дереве для строки длины <tex>n + 1</tex>, у которых хотя бы один из детей - лист. | Рассмотрим все вершины в дереве для строки длины <tex>n + 1</tex>, у которых хотя бы один из детей - лист. | ||
| − | Если среди них есть вершина, у которой более двух детей, отрежем от нее лист. Получим дерево с <tex>n</tex> листьями, удовлетворяющее условию леммы по индукционному предположению, причем в нем количество внутренних вершин равно количеству внутренних вершин в исходном дереве. Тогда у полученного дерева менее <tex>n</tex> внутренних вершин, значит в исходном дереве количество внутренних вершин | + | Если среди них есть вершина, у которой более двух детей, отрежем от нее лист. Получим дерево с <tex>n</tex> листьями, удовлетворяющее условию леммы по индукционному предположению, причем в нем количество внутренних вершин равно количеству внутренних вершин в исходном дереве. Тогда у полученного дерева менее <tex>n</tex> внутренних вершин, значит в исходном дереве количество внутренних вершин меньше количества листьев. |
Иначе среди этих вершин есть вершина, у которой оба ребенка - листья. Отрежем оба этих листа, получим дерево с <tex>n</tex> листьями, удовлетворяющее условию леммы, количество внутренних вершин которого на <tex>1</tex> меньше количества внутренних вершин в исходном дереве. Тогда, по индукционному предположению, у полученного дерева менее <tex>n</tex> внутренних вершин, значит в исходном дереве количество внутренних вершин меньше <tex>n + 1</tex>. | Иначе среди этих вершин есть вершина, у которой оба ребенка - листья. Отрежем оба этих листа, получим дерево с <tex>n</tex> листьями, удовлетворяющее условию леммы, количество внутренних вершин которого на <tex>1</tex> меньше количества внутренних вершин в исходном дереве. Тогда, по индукционному предположению, у полученного дерева менее <tex>n</tex> внутренних вершин, значит в исходном дереве количество внутренних вершин меньше <tex>n + 1</tex>. | ||
| Строка 36: | Строка 36: | ||
==Занимаемая память== | ==Занимаемая память== | ||
| − | + | Так как любое суффиксное дерево удовлетворяет условиям леммы (у каждой вершины не менее двух детей), то количество внутренних вершин в нем меньше количества листьев, равного <tex>n</tex>. Значит, для его хранения требуется <tex>O(n|\Sigma|)</tex> памяти. | |
==Построение суффиксного дерева== | ==Построение суффиксного дерева== | ||
| Строка 43: | Строка 43: | ||
insert(<tex>i, n</tex>) //добавляем суффикс, начинающийся с него | insert(<tex>i, n</tex>) //добавляем суффикс, начинающийся с него | ||
| − | insert(l,r) | + | insert(l,r) |
<tex> cur \leftarrow root </tex> //инициализируем текущую вершину корнем | <tex> cur \leftarrow root </tex> //инициализируем текущую вершину корнем | ||
'''while''' (<tex> i < r </tex>) | '''while''' (<tex> i < r </tex>) | ||
| Строка 52: | Строка 52: | ||
<tex>finish \leftarrow go[cur][s[i]].r </tex> | <tex>finish \leftarrow go[cur][s[i]].r </tex> | ||
'''for''' <tex> j = start </tex> '''to''' <tex> finish </tex> //для каждого символа на ребре из текущей вершины | '''for''' <tex> j = start </tex> '''to''' <tex> finish </tex> //для каждого символа на ребре из текущей вершины | ||
| − | '''if''' <tex>s[i+j-start] <>s[j] </tex> //нашли не совпадающий символ | + | '''if''' <tex>s[i+j-start] <>s[j] </tex> //если нашли не совпадающий символ |
'''разбить ребро''' | '''разбить ребро''' | ||
'''break''' | '''break''' | ||
| Строка 61: | Строка 61: | ||
Этот алгоритм работает за время <tex>O(n^2)</tex>, однако существует [[Алгоритм Укконена| алгоритм Укконена]], позволяющий построить дерево за время <tex>O(n)</tex>. | Этот алгоритм работает за время <tex>O(n^2)</tex>, однако существует [[Алгоритм Укконена| алгоритм Укконена]], позволяющий построить дерево за время <tex>O(n)</tex>. | ||
| − | ==Использование== | + | ==Использование сжатого суффиксного дерева== |
Суффиксное дерево позволяет за линейное время найти: | Суффиксное дерево позволяет за линейное время найти: | ||
* Количество различных подстрок данной строки | * Количество различных подстрок данной строки | ||
Версия 12:23, 8 мая 2012
Суффиксный бор — удобная структура для поиска подстроки в строке, но занимающая много места в памяти. Рассмотрим все такие пути от до в суффиксном боре, в которых каждая вершина имеет только одного сына. Такой путь можно сжать до одного ребра , пометив его всеми встречающимися на пути символами. Получившееся дерево носит название сжатое суффиксное дерево.
Содержание
Определение
Суффиксное дерево (сжатое суффиксное дерево) для строки (где ) — ориентированное дерево с листьями, каждая внутренняя вершина которого имеет не меньше двух детей, а каждое ребро помечено непустой подстрокой строки и символом, с которого начинается эта подстрока. При этом два ребра, выходящие из одной вершины, не могут иметь одинаковых символьных пометок. Такое дерево содержит все суффиксы строки : для каждого листа конкатенация подстрок на ребрах пути от корня к этому листу составляет суффикс, который начинается в позиции , то есть . Иными словами, каждый суффикс строки заканчивается точно в листе и нигде кроме листа, как и в суффиксном боре.
Защитный символ
Определение суффиксного дерева не гарантирует, что такое дерево существует для любой строки . Если один суффикс строки совпадает с префиксом другого, то построить суффиксное дерево, удовлетворяющее данному выше определению, невозможно. Например, для строки суффикс является префиксом суффикса Во избежание этого в конце строки добавляется символ, не входящий в исходный алфавит. Такой символ называется защитным. Как правило, это . Любой суффикс строки с защитным символом заканчивается в листе и только в листе, т.к. он не встречается в строке нигде, кроме позиции последнего символа.
Далее - длина строки с защитным символом.
Хранение суффиксного дерева
Каждое ребро суффиксного дерева помечается подстрокой исходной строки . Но лучше для него хранить не саму подстроку, а индексы ее начала и конца в исходной строке — . Итак, с каждым ребром дерева ассоциируются две инцидентные ей вершины, символ, с которого начинается подстрока на ребре и два числа . Представим дерево как массив , где — количество вершин в дереве, - мощность алфавита. Каждая ячейка массива содержит информацию о том, в какую вершину ведет ое ребро по ому символу и индексы подстроки на ребре. Очевидно, такое дерево занимает памяти.
Количество вершин
В сжатом суффиксном дереве содержится листьев, т.к. строка содержит ровно суффиксов. Рассмотрим теперь количество внутренних вершин такого дерева.
| Лемма: |
Количество внутренних вершин дерева, каждая из которых имеет не менее двух детей, меньше количества листьев. |
| Доказательство: |
|
Докажем лемму индукцией по количеству листьев . База При в дереве одна внутренняя вершина - верно. Переход Рассмотрим все вершины в дереве для строки длины , у которых хотя бы один из детей - лист. Если среди них есть вершина, у которой более двух детей, отрежем от нее лист. Получим дерево с листьями, удовлетворяющее условию леммы по индукционному предположению, причем в нем количество внутренних вершин равно количеству внутренних вершин в исходном дереве. Тогда у полученного дерева менее внутренних вершин, значит в исходном дереве количество внутренних вершин меньше количества листьев. Иначе среди этих вершин есть вершина, у которой оба ребенка - листья. Отрежем оба этих листа, получим дерево с листьями, удовлетворяющее условию леммы, количество внутренних вершин которого на меньше количества внутренних вершин в исходном дереве. Тогда, по индукционному предположению, у полученного дерева менее внутренних вершин, значит в исходном дереве количество внутренних вершин меньше . |
Занимаемая память
Так как любое суффиксное дерево удовлетворяет условиям леммы (у каждой вершины не менее двух детей), то количество внутренних вершин в нем меньше количества листьев, равного . Значит, для его хранения требуется памяти.
Построение суффиксного дерева
Рассмотрим наивный алгоритм построения суффиксного дерева:
for to do //для каждого символа строки insert() //добавляем суффикс, начинающийся с него
insert(l,r)
//инициализируем текущую вершину корнем
while ()
if //если мы не можем пойти из вершины по символу
create_vertex() //создаем новую вершину
else
for to //для каждого символа на ребре из текущей вершины
if //если нашли не совпадающий символ
разбить ребро
break
if ребро не разбивали
//переходим по ребру
//двигаемся по суффиксу на длину подстроки, записанной на ребре
Этот алгоритм работает за время , однако существует алгоритм Укконена, позволяющий построить дерево за время .
Использование сжатого суффиксного дерева
Суффиксное дерево позволяет за линейное время найти:
- Количество различных подстрок данной строки
- Наибольшую общую подстроку двух строк
- Суффиксный массив и массив (longest common prefix) исходной строки
Источники
- Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.