Ортогональный поиск

Простейший случай

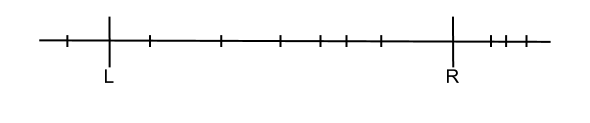
Пусть дана прямая с точками на ней и отрезок. Точки даны в отсортированном порядке. Необходимо указать, какие из изначальных точек лежат на этом отрезке.

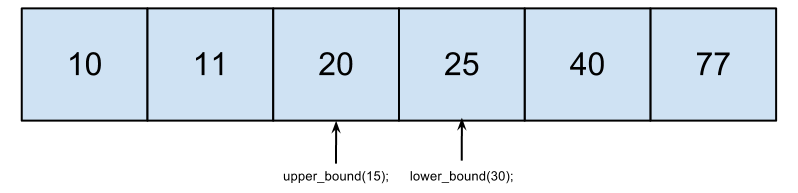
Данная задача решается с помощью функций из STL - upper_bound и lower_bound.

upper_bound возвращает наименьшее значение больше данного, lower_bound - наибольшее значение меньше данного.

Рассмотрим на примере:

Код реализации:

template<class RauIter, class OutIter, class Scalar> OutIter range_search(RauIter p, RauIter q, OutIter out)
{
   return std::copy(lower_bound(p, q, l), upper_bound(p, q, r), out);
}

Сбалансированное дерево поиска

Переходим к двумерному случаю. Пусть дано некоторое множество точек на плоскости. Нам необходимо ответить, какие именно из них лежат в некотором заданном прямоугольнике.

Для этого возьмем любое сбалансированное дерево поиска и наполним его точками [math](x, y)[/math] из множества. В качестве ключа будет использоваться [math]x[/math]-координата точки. Теперь слегка модернизируем дерево: в каждой вершине дерева будем хранить отсортированный по [math]y[/math]-координате массив точек, которые содержатся в соответствующем поддереве. В такой структуре данных поиск точек в заданном прямоугольнике [math](x_{min}, x_{max}) \times (y_{min}, y_{max})[/math] будет выглядеть следующим образом:

1. Выберем из дерева поиска те точки, [math]x[/math]-координата которых лежит в интервале [math](x_{min}, x_{max})[/math]. Сделаем это точно так же, как делается запрос сверху в дереве отрезков. Из аналогии с деревом отрезков следует, что мы ответ мы получим в виде [math]O(\log n)[/math] поддеревьев дерева поиска.
2. Для каждого из полученных поддеревьев обратимся к массиву содержащихся в нем точек и запустим от него приведенную выше функцию [math]range{\_}search(y_{min}, y_{max})[/math]. Все полученные таким образом точки и будут составлять ответ.

Каждая из функций [math]range{\_}search(y_{min}, y_{max})[/math] будет работать в худшем случае за [math]O(\log n)[/math], отсюда получаем итоговое время выполнения запроса [math]O(\log^2 n)[/math].