Разрешение коллизий — различия между версиями
SergeyN (обсуждение | вклад) (→Стратегии поиска) |
SergeyN (обсуждение | вклад) (→Стратегии поиска) |
||
| Строка 8: | Строка 8: | ||
'' Последовательный поиск '' | '' Последовательный поиск '' | ||
| − | [[Файл:hashtables1.png|thumb| | + | [[Файл:hashtables1.png|thumb|280px|right|Последовательный поиск, частный случай линейного поиска.]] |
При попытке добавить элемент в занятую ячейку <tex>i</tex> начинаем последовательно просматривать ячейки <tex>i+1, i+2, i+3</tex> и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. | При попытке добавить элемент в занятую ячейку <tex>i</tex> начинаем последовательно просматривать ячейки <tex>i+1, i+2, i+3</tex> и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. | ||
'' Линейный поиск '' | '' Линейный поиск '' | ||
| + | [[Файл:hashtables2.png|thumb|280px|right|Линейный поиск с шагом q.]] | ||
Выбираем шаг <tex>q</tex>. При попытке добавить элемент в занятую ячейку <tex>i</tex> начинаем последовательно просматривать ячейки <tex>i+(1 \cdot q), i+(2 \cdot q), i+(3 \cdot q)</tex> и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. | Выбираем шаг <tex>q</tex>. При попытке добавить элемент в занятую ячейку <tex>i</tex> начинаем последовательно просматривать ячейки <tex>i+(1 \cdot q), i+(2 \cdot q), i+(3 \cdot q)</tex> и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. | ||
| Строка 18: | Строка 19: | ||
'' Квадратичный поиск '' | '' Квадратичный поиск '' | ||
| + | [[Файл:hashtables3.png|thumb|280px|right|Квадратичный поиск.]] | ||
Шаг <tex>q</tex> не фиксирован, а изменяется квадратично: <tex>q = 1,4,9,16...</tex>. Соответственно при попытке добавить элемент в занятую ячейку <tex>i</tex> начинаем последовательно просматривать ячейки <tex> i+1, i+4, i+9</tex> и так далее, пока не найдём свободную ячейку. | Шаг <tex>q</tex> не фиксирован, а изменяется квадратично: <tex>q = 1,4,9,16...</tex>. Соответственно при попытке добавить элемент в занятую ячейку <tex>i</tex> начинаем последовательно просматривать ячейки <tex> i+1, i+4, i+9</tex> и так далее, пока не найдём свободную ячейку. | ||
Версия 20:59, 28 мая 2012
Поиск свободного места при закрытом хешировании - задача, возникающая при создании хеш-таблицы, использующей так называемое закрытое хеширование.
При использовании открытого хеширования такой проблемы не возникает, так как там в каждой ячейке хранится список всех элементов. При добавлении необходимо просто добавить элемент в начало списка.
Закрытое хеширование работает иначе: в каждой ячейке хеш-таблицы хранится только один элемент. Тогда при добавлении, если ячейка свободна, мы просто записываем добавляемый элемент в эту ячейку. Однако если эта ячейка занята - необходимо поместить добавляемый элемент в какую-нибудь другую свободную ячейку. Такие ситуации нередки, так как невозможно использовать хеш-функцию, не дающую коллизий, а каждой ячейке таблицы соответствует одно значение хеш-функции. Далее мы рассмотрим несколько стратегий поиска свободного места в данном случае.
Содержание
Стратегии поиска
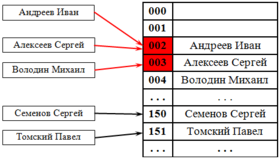
Последовательный поиск
При попытке добавить элемент в занятую ячейку начинаем последовательно просматривать ячейки и так далее, пока не найдём свободную ячейку. В неё и запишем элемент.
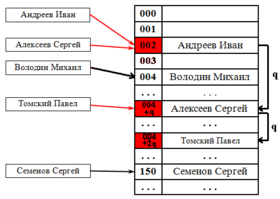
Линейный поиск
Выбираем шаг . При попытке добавить элемент в занятую ячейку начинаем последовательно просматривать ячейки и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. По сути последовательный поиск - частный случай линейного, где .
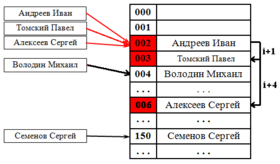
Квадратичный поиск
Шаг не фиксирован, а изменяется квадратично: . Соответственно при попытке добавить элемент в занятую ячейку начинаем последовательно просматривать ячейки и так далее, пока не найдём свободную ячейку.
Возможные проблемы
При поиске элемента может получится так, что мы дойдём до конца таблицы. Обычно поиск продолжается, начиная с другого конца. Однако, если мы придём в ту ячейку, откуда начинался поиск, то добавить элемент в текущую таблицу будет невозможно и необходимо провести операцию перехеширования.
Так же может случиться, что не останется свободных ячеек в хеш-таблице. Поэтому, при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.
Проверка наличия элемента в таблице
Проверка осуществляется аналогично добавлению: мы проверяем ячейку и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку.
Проблемы закрытого хеширования
Проблем две - крайне нетривиальное удаление элемента из таблицы и образование кластеров. Кластер - последовательность занятых клеток. Их наличие замедляет все операции с хеш-таблицей: при добавлении требуется перебирать всё больше элементов, при проверке тоже. Чем больше в таблице элементов, тем больше в ней кластеры и тем выше вероятность того, что добавляемый элемент попадёт в кластер. Для защиты от кластеризации используется двойное хеширование и хеширование кукушки.
Литература
- Хеширование — Википедия
- Хеш-таблица — Википедия
- Т. Кормен, Ч. Лейзерсон, Р. Ривест, Алгоритмы: построение и анализ, 2-е издание, Издательский дом "Вильямс", 2005 год, стр. 282