Сеть Бетчера — различия между версиями
Murtaught (обсуждение | вклад) (Объединяющая сеть) |
Murtaught (обсуждение | вклад) (Сортирующая сеть) |
||
| Строка 1: | Строка 1: | ||
{{В разработке}} | {{В разработке}} | ||
==Определение== | ==Определение== | ||
| − | <b>Сеть Бетчера (Batcher odd-even mergesort)</b> {{---}} сортирующая сеть размером <tex>O(n \log^2n)</tex> и глубиной <tex>O(\log^2n)</tex>, где <tex>n</tex> {{---}} количество элементов для сортировки. | + | <b>Сеть Бетчера <i>(Batcher odd-even mergesort)</i></b> {{---}} сортирующая сеть размером <tex>O(n \log^2n)</tex> и глубиной <tex>O(\log^2n)</tex>, где <tex>n</tex> {{---}} количество элементов для сортировки. |
==Конструирование сети== | ==Конструирование сети== | ||
| Строка 13: | Строка 13: | ||
<b>Нуль-единичные битонические последовательности</b> {{---}} последовательности вида <tex>0^i1^j0^k</tex> или <tex>1^i0^j1^k</tex> для целых <tex>i,j,k\ge0</tex>, где <tex>1^i</tex> или <tex>0^i</tex> обозначает <tex>i</tex> идущих подряд единиц или нулей соответственно.}} | <b>Нуль-единичные битонические последовательности</b> {{---}} последовательности вида <tex>0^i1^j0^k</tex> или <tex>1^i0^j1^k</tex> для целых <tex>i,j,k\ge0</tex>, где <tex>1^i</tex> или <tex>0^i</tex> обозначает <tex>i</tex> идущих подряд единиц или нулей соответственно.}} | ||
В качестве примеров нуль-единичной битонической последовательности можно привести последовательности <tex>00111000</tex>, <tex>11000111</tex>, <tex>1110</tex>, <tex>1</tex>, <tex>000</tex>. <br> | В качестве примеров нуль-единичной битонической последовательности можно привести последовательности <tex>00111000</tex>, <tex>11000111</tex>, <tex>1110</tex>, <tex>1</tex>, <tex>000</tex>. <br> | ||
| − | С первого взгляда битонические последовательности могут показаться бесполезными в деле построения сортирующих сетей, но на самом деле они обладают одним полезным свойством: если соединить вместе две отсортированные последовательности, причем одна из них должна быть отсортировала по возрастанию, а другая по убыванию {{---}} то получится битоническая последовательность. Далее | + | С первого взгляда битонические последовательности могут показаться бесполезными в деле построения сортирующих сетей, но на самом деле они обладают одним полезным свойством: если соединить вместе две отсортированные последовательности, причем одна из них должна быть отсортировала по возрастанию, а другая по убыванию {{---}} то получится битоническая последовательность. Далее этому свойству будет найдено применение. |
===Битонический сортировщик=== | ===Битонический сортировщик=== | ||
| − | + | Построим сеть, которая эффективно сортирует все битонические последовательности {{---}} т.н. <b>битонический сортировщик</b>. <br> | |
{| <!-- Какие-то адовые костыли только чтобы разместить картинку справа от текста --> | {| <!-- Какие-то адовые костыли только чтобы разместить картинку справа от текста --> | ||
| | | | ||
====Полуфильтр==== | ====Полуфильтр==== | ||
| − | Основной элемент битонического сортировщика называется <b>полуфильтром< | + | Основной элемент битонического сортировщика называется <b>полуфильтром <i>(half-cleaner)</i></b>. |
| − | Каждый полуфильтр {{---}} сравнивающая сеть единичной глубины, в которой <tex>i</tex>-й входной провод сравнивается со входным проводом с номером <tex>\frac{n}{2} + i</tex>, где <tex>i=1,2,...,\frac{n}{2}</tex> ( | + | Каждый полуфильтр {{---}} сравнивающая сеть единичной глубины, в которой <tex>i</tex>-й входной провод сравнивается со входным проводом с номером <tex>\frac{n}{2} + i</tex>, где <tex>i=1,2,...,\frac{n}{2}</tex> (пусть количество входов <tex>n</tex> {{---}} чётное).<br> |
| − | [[Файл:Half-Cleaner1.png|250px|center|thumb|Рис.1 Полуфильтр для 8 проводов]] | + | [[Файл:Half-Cleaner1.png|250px|center|thumb|Рис.1 Полуфильтр для 8 проводов.]] |
{{Лемма|statement= | {{Лемма|statement= | ||
| Строка 31: | Строка 31: | ||
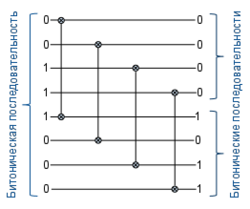
Для всех <tex>i=1,2,...,\frac{n}{2}</tex> полуфильтр сравнивает провода с номерами <tex>i</tex> и <tex>i+\frac{n}{2}</tex>. Без потери общности будем рассматривать входную последовательность вида <tex>0...01...10...0</tex> (для последовательности вида <tex>1...10...01...1</tex> рассуждения аналогичны). В зависимости от того в каком блоке из последовательно расположенных нулей и единиц находится средняя точка <tex>\frac{n}{2}</tex> входной последовательности, можно выделить 3 случая, причем один из случаев (когда средняя точка попадает на блок из единиц) можно разбить еще на 2 случая. Все 4 случая разобраны на рис. 2. Для каждого из ни лемма выполняется. | Для всех <tex>i=1,2,...,\frac{n}{2}</tex> полуфильтр сравнивает провода с номерами <tex>i</tex> и <tex>i+\frac{n}{2}</tex>. Без потери общности будем рассматривать входную последовательность вида <tex>0...01...10...0</tex> (для последовательности вида <tex>1...10...01...1</tex> рассуждения аналогичны). В зависимости от того в каком блоке из последовательно расположенных нулей и единиц находится средняя точка <tex>\frac{n}{2}</tex> входной последовательности, можно выделить 3 случая, причем один из случаев (когда средняя точка попадает на блок из единиц) можно разбить еще на 2 случая. Все 4 случая разобраны на рис. 2. Для каждого из ни лемма выполняется. | ||
}} | }} | ||
| − | ||[[Файл:Half-Cleaner-proof.png|200px|right|thumb|Рис.2 Все случаи попадания битонической последовательности на полуфильтр]] | + | ||[[Файл:Half-Cleaner-proof.png|200px|right|thumb|Рис.2 Все случаи попадания битонической последовательности на полуфильтр.]] |
|} | |} | ||
| Строка 37: | Строка 37: | ||
| | | | ||
====Битонический сортировщик==== | ====Битонический сортировщик==== | ||
| − | Теперь | + | Теперь используем полуфильтры для сортировки битонических последовательностей. Как только что было доказано, один полуфильтр разделяет битоническую последовательность на две равные части, одна из которых однородна, а другая сама по себе является битонической последовательностью, причем части расположены в правильном порядке. Тогда мы можем каждую часть снова отправить в полуфильтр вдвое меньшего размера, чем предыдущий. Затем, если нужно, четыре получившихся части снова отправить в полуфильтры и так далее, пока количество проводов в одной части больше <tex>1</tex>. |
Так можно построить сеть для числа входов, являющегося степенью <tex>2</tex>. Поскольку каждый вертикальный ряд полуфильтров вдвое сокращает число входов, которые необходимо отсортировать, глубина всей сети равна <tex>\log_{2}n</tex>, где <tex>n</tex> {{---}} число входов. | Так можно построить сеть для числа входов, являющегося степенью <tex>2</tex>. Поскольку каждый вертикальный ряд полуфильтров вдвое сокращает число входов, которые необходимо отсортировать, глубина всей сети равна <tex>\log_{2}n</tex>, где <tex>n</tex> {{---}} число входов. | ||
| Строка 49: | Строка 49: | ||
|definition= | |definition= | ||
<b>Объединяющая сеть <i>(Merger)</i></b> {{---}} сеть компараторов, объединяющая две отсортированные входные последовательности в одну отсортированную выходную последовательность.}} | <b>Объединяющая сеть <i>(Merger)</i></b> {{---}} сеть компараторов, объединяющая две отсортированные входные последовательности в одну отсортированную выходную последовательность.}} | ||
| − | Построим объединяющую сеть на основе битонического сортировщика. Для этого рассмотрим наши отсортированные | + | Построим объединяющую сеть на основе битонического сортировщика. Для этого рассмотрим наши отсортированные входные последовательности: <br> |
| − | Отсортированная последовательность имеет вид <tex>0^i1^j</tex> для целых <tex>i, j\ge0</tex>. Запишем две входные последовательности как <tex>0^i1^j</tex> и <tex>0^k1^l</tex>. Если перевернуть вторую последовательность, получится отсортированная по невозрастанию последовательность <tex>1^l0^k</tex>. Если теперь записать | + | Отсортированная последовательность имеет вид <tex>0^i1^j</tex> для целых <tex>i, j\ge0</tex>. Запишем две входные последовательности как <tex>0^i1^j</tex> и <tex>0^k1^l</tex>. Если перевернуть вторую последовательность, получится отсортированная по невозрастанию последовательность <tex>1^l0^k</tex>. Если теперь записать первую и перевернутую вторую последовательности подряд, получится битоническая последовательность <tex>0^i1^{j+l}0^k</tex>, которую можно отсортировать в битоническом сортировщике с глубиной <tex>O(\log{n})</tex>. |
| − | |||
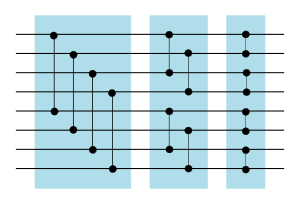
| − | + | Объединяющая сеть является ничем иным как битоническим сортировщиком. Единственное отличие в том, что половина входных проводов расположена в обратном порядке (предполагается, что мы объединяем две сети одинакового размера <tex>\frac{n}{2}</tex>). Поэтому первый полуфильтр будет отличаться от остальных {{---}} он будет соединять <tex>i</tex>-ый провод не с <tex>\frac{n}{2} + i</tex>-ым, а с <tex>n-i+1</tex>-ым проводом. Пример объединяющей сети для 8 проводов приведен на рисунке 4. | |
| − | ||[[Файл:Merger_8.png|294px|right|thumb|Рис.4 | + | ||[[Файл:Merger_8.png|294px|right|thumb|Рис.4 Сеть, объединяющая две отсортированные последовательности из 4 чисел в одну отсортированную последовательность из 8 чисел.]] |
| + | |} | ||
| + | |||
| + | {| | ||
| + | | | ||
| + | === Сортирующая сеть === | ||
| + | Теперь, с помощью описанных выше объединяющих сетей мы построим параллельную версию [[сортировка слиянием|сортировки слиянием]]. <br> | ||
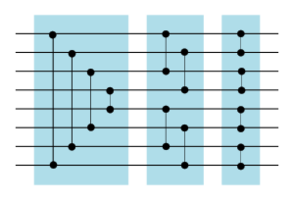
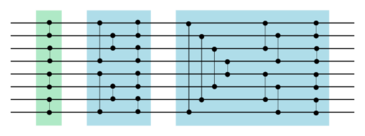
| + | Пусть мы хотим отсортировать <tex>n=2^k</tex> входов, <tex>k</tex> {{---}} целое и <tex>k \ge0</tex>. Для этого сначала отсортируем пары проводов, поставив в первом слое компаратор между <tex>i</tex>-ым и <tex>i+1</tex>-ым проводом для нечетных <tex>i < n</tex>. Затем с помощью объединяющих сетей параллельно объединим отсортированные пары проводов в отсортированные четверки. Затем объединим отсортированные четверки в отсортированные восьмерки. И так далее, пока на выходе очередной объединяющей сети не будет <tex>n</tex> проводов. <br> | ||
| + | Пример такой сети приведен на рисунке 5. | ||
| + | ||[[Файл:Sorter_8.png|365px|right|thumb|Рис.5 Сортирующая сеть для 8 проводов.]] | ||
|} | |} | ||
==Источники== | ==Источники== | ||
Версия 15:15, 5 июня 2012
Содержание
Определение
Сеть Бетчера (Batcher odd-even mergesort) — сортирующая сеть размером и глубиной , где — количество элементов для сортировки.
Конструирование сети
Для начала введем понятие битонической последовательности:
| Определение: |
| Битонической последовательностью называется последовательность, которая сначала монотонно возрастает, а затем монотонно убывает, или последовательность, которая приводится к такому виду путем циклического сдвига. |
Сейчас мы будем рассматривать только нуль-единичные битонические последовательности:
| Определение: |
| Нуль-единичные битонические последовательности — последовательности вида или для целых , где или обозначает идущих подряд единиц или нулей соответственно. |
В качестве примеров нуль-единичной битонической последовательности можно привести последовательности , , , , .
С первого взгляда битонические последовательности могут показаться бесполезными в деле построения сортирующих сетей, но на самом деле они обладают одним полезным свойством: если соединить вместе две отсортированные последовательности, причем одна из них должна быть отсортировала по возрастанию, а другая по убыванию — то получится битоническая последовательность. Далее этому свойству будет найдено применение.
Битонический сортировщик
Построим сеть, которая эффективно сортирует все битонические последовательности — т.н. битонический сортировщик.
ПолуфильтрОсновной элемент битонического сортировщика называется полуфильтром (half-cleaner).
Каждый полуфильтр — сравнивающая сеть единичной глубины, в которой -й входной провод сравнивается со входным проводом с номером , где (пусть количество входов — чётное).
|
Битонический сортировщикТеперь используем полуфильтры для сортировки битонических последовательностей. Как только что было доказано, один полуфильтр разделяет битоническую последовательность на две равные части, одна из которых однородна, а другая сама по себе является битонической последовательностью, причем части расположены в правильном порядке. Тогда мы можем каждую часть снова отправить в полуфильтр вдвое меньшего размера, чем предыдущий. Затем, если нужно, четыре получившихся части снова отправить в полуфильтры и так далее, пока количество проводов в одной части больше . Так можно построить сеть для числа входов, являющегося степенью . Поскольку каждый вертикальный ряд полуфильтров вдвое сокращает число входов, которые необходимо отсортировать, глубина всей сети равна , где — число входов. |
Объединяющая сеть
Битонический сортировщик находит своё применение в конструкции так называемой объединяющей сети.
Построим объединяющую сеть на основе битонического сортировщика. Для этого рассмотрим наши отсортированные входные последовательности: Объединяющая сеть является ничем иным как битоническим сортировщиком. Единственное отличие в том, что половина входных проводов расположена в обратном порядке (предполагается, что мы объединяем две сети одинакового размера ). Поэтому первый полуфильтр будет отличаться от остальных — он будет соединять -ый провод не с -ым, а с -ым проводом. Пример объединяющей сети для 8 проводов приведен на рисунке 4. |
Сортирующая сетьТеперь, с помощью описанных выше объединяющих сетей мы построим параллельную версию сортировки слиянием. |
Источники
- Wikipedia — Batcher odd-even mergesort
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2005. — С. 808—818.