Персистентный стек — различия между версиями
Yurik (обсуждение | вклад) |
Yurik (обсуждение | вклад) |
||
| Строка 23: | Строка 23: | ||
* Пусть изначально у нас есть один пустой стек. Запишем его в массив. | * Пусть изначально у нас есть один пустой стек. Запишем его в массив. | ||
| + | [[Файл:стек1.png|500px|nothumb|right|]] | ||
{| border = 1; cellspacing = 0; class="wikitable" | {| border = 1; cellspacing = 0; class="wikitable" | ||
|- align = "center" | |- align = "center" | ||
| Строка 37: | Строка 38: | ||
* Далее выполним <tex>push(1, 3)</tex>. Создается новая вершина со значением 3, ссылающаяся на 1-ую, помещаем ее во 2-ую ячейку массива: | * Далее выполним <tex>push(1, 3)</tex>. Создается новая вершина со значением 3, ссылающаяся на 1-ую, помещаем ее во 2-ую ячейку массива: | ||
| + | [[Файл:стек2.png|500px|nothumb|right|]] | ||
{| border = 1; cellspacing = 0; class="wikitable" | {| border = 1; cellspacing = 0; class="wikitable" | ||
|- align = "center" | |- align = "center" | ||
| Строка 54: | Строка 56: | ||
* Аналогично выполним <tex>push(2, 5)</tex>: | * Аналогично выполним <tex>push(2, 5)</tex>: | ||
| + | [[Файл:стек3.png|500px|nothumb|right|]] | ||
{| border = 1; cellspacing = 0; class="wikitable" | {| border = 1; cellspacing = 0; class="wikitable" | ||
|- align = "center" | |- align = "center" | ||
| Строка 74: | Строка 77: | ||
* Выполним <tex>pop(3)</tex>. он возвращает 5 и копирует 2-ую вершину. | * Выполним <tex>pop(3)</tex>. он возвращает 5 и копирует 2-ую вершину. | ||
| + | [[Файл:стек4.png|500px|nothumb|right|]] | ||
{| border = 1; cellspacing = 0; class="wikitable" | {| border = 1; cellspacing = 0; class="wikitable" | ||
|- align = "center" | |- align = "center" | ||
| Строка 97: | Строка 101: | ||
* Так будет выглядеть массив после последовательности операций <tex>push(3, 6), push(5, 1), pop(4), pop(5), push(7, 9):</tex> | * Так будет выглядеть массив после последовательности операций <tex>push(3, 6), push(5, 1), pop(4), pop(5), push(7, 9):</tex> | ||
| − | + | [[Файл:стек.png|500px|nothumb|right|]] | |
{| border = 1; cellspacing = 0; class="wikitable" | {| border = 1; cellspacing = 0; class="wikitable" | ||
|- align = "center" | |- align = "center" | ||
| Строка 133: | Строка 137: | ||
|7 | |7 | ||
|} | |} | ||
| − | + | ||
В итоге мы имеем доступ ко всем версиям стека за <tex>O(1)</tex> времени и <tex>O(n)</tex> памяти. | В итоге мы имеем доступ ко всем версиям стека за <tex>O(1)</tex> времени и <tex>O(n)</tex> памяти. | ||
| + | |||
| + | |||
== См. также== | == См. также== | ||
Версия 19:16, 8 июня 2012
Персистентными структурами данных называются такие структуры, хранящие все свои промежуточные версии.
Рассмотрим такую структуру на примере стека.
Наивная реализация
Самое простое и очевидное решение этой задачи — честное копирование стека при каждой операции.
Очевидно, это не самое эффективное решение. Сложность одной операции составляет и количество требуемой памяти — .
Эффективная реализация
Попробуем решить задачу эффективнее. Заведем массив запросов, модифицирующих стек.
У каждого элемента массива будет 2 поля: значение в вершине стека и индекс предыдущей версии стека.
Тогда операции push и pop будут иметь следующий вид:
- — добавляет элемент х в стек с номером i, результирующий стек будет иметь номер .
- — возвращает значение, хранящееся в элементе с номером i и копирует элемент, предыдущий для него.
результирующий стек будет иметь номер .
Пример
- Пусть изначально у нас есть один пустой стек. Запишем его в массив.
| index | 1 |
|---|---|
| value | |
| prev |
- Далее выполним . Создается новая вершина со значением 3, ссылающаяся на 1-ую, помещаем ее во 2-ую ячейку массива:
| index | 1 | 2 |
|---|---|---|
| value | 3 | |
| prev | 1 |
- Аналогично выполним :
| index | 1 | 2 | 3 |
|---|---|---|---|
| value | 3 | 5 | |
| prev | 1 | 2 |
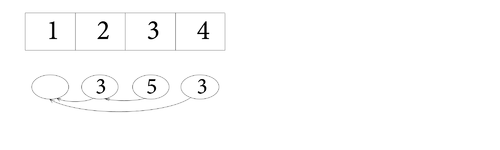
- Выполним . он возвращает 5 и копирует 2-ую вершину.
| index | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| value | 3 | 5 | 3 | |
| prev | 1 | 2 | 1 |
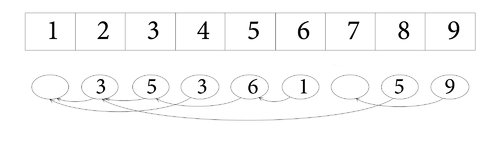
- Так будет выглядеть массив после последовательности операций
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| value | 3 | 5 | 3 | 6 | 1 | 5 | 9 | ||
| prev | 1 | 2 | 1 | 3 | 5 | 2 | 7 |
В итоге мы имеем доступ ко всем версиям стека за времени и памяти.