Сортировка кучей — различия между версиями
| Строка 24: | Строка 24: | ||
{|align="right" | {|align="right" | ||
|-valign="top" | |-valign="top" | ||
| − | |[[Файл:heap1.png| | + | |[[Файл:heap1.png|155px|thumb|Строим кучу]] |
| − | |[[Файл:heap2.png| | + | |[[Файл:heap2.png|155px|thumb|Первый проход]] |
| − | |[[Файл:heap3.png| | + | |[[Файл:heap3.png|155px|thumb|Строим новую кучу]] |
|- | |- | ||
| − | |[[Файл:heap4.png| | + | |[[Файл:heap4.png|155px|thumb|Второй проход]] |
| − | |[[Файл:heap5.png| | + | |[[Файл:heap5.png|155px|thumb|Третий проход]] |
| − | |[[Файл:heap6.png| | + | |[[Файл:heap6.png|155px|thumb|Четвертый проход]] |
|} | |} | ||
Версия 16:34, 10 июня 2012
Сортировка кучей, пирамидальная сортировка (англ. Heapsort) — алгоритм сортировки, использующий структуру данных двоичная куча. Это неустойчивый алгоритм сортировки с временем работы , где — количество элементов для сортировки, и использующий дополнительной памяти.
Содержание
Алгоритм
Необходимо отсортировать массив , размером . Построим на базе этого массива за невозрастающую кучу. Так как по свойству кучи максимальный элемент находится в корне, то, поменявшись его местами с , он встанет на свое место. Далее вызовем процедуру , предварительно уменьшив на . Она за просеет на нужное место и сформирует новую кучу (так как мы уменьшили ее размер, то куча располагается с по , а элемент находится на своем месте). Повторим эту процедуру для новой кучи, только корень будет менять местами не с , а с . Делая аналогичные действия, пока не станет равен , мы будем ставить наибольшее из оставшихся чисел в конец не отсортированной части. Очевидно, что таким образом, мы получим отсортированный массив.
Реализация
— массив, который необходимо отсортировать; — количество элементов в нем; - процедура, которая строит из передаваемого массива невозрастающую кучу в этом же массиве; — процедура, которая просеивает вниз элемент в куче из элементов, находящихся в начале массива .
heapsort(A)
build_heap(A);
heap_size = A.size;
for i = 0 to n - 2
swap(A[0], A[n - 1 - i]);
heap_size--;
sift_down(A, 0, heap_size);
Сложность
Операция работает за . Всего цикл выполняется раз. Таким образом сложность сортировки кучей является .
Пример
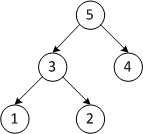
Пусть дана последовательность из элементов .
| Массив | Описание шага | |
|---|---|---|
| 5 3 4 1 2 | Строим кучу из исходного массива | |
| Первый проход | ||
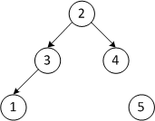
| 2 3 4 1 5 | Меняем местами первый и последний элементы | |
| 4 3 2 1 5 | Строим кучу из первых четырех элементов | |
| Второй проход | ||
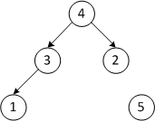
| 1 3 2 4 5 | Меняем местами первый и четвертый элементы | |
| 3 1 2 4 5 | Строим кучу из первых трех элементов | |
| Третий проход | ||
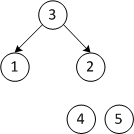
| 2 1 3 4 5 | Меняем местами первый и третий элементы | |
| 2 1 3 4 5 | Строим кучу из двух элементов | |
| Четвертый проход | ||
| 1 2 3 4 5 | Меняем местами первый и второй элементы | |
| 1 2 3 4 5 | Массив отсортирован | |
Ссылки
Литература
- Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, 2-е издание. М.: Издательский дом "Вильямс", 2005. ISBN 5-8459-0857-4