Карманная сортировка — различия между версиями
Daniel (обсуждение | вклад) |
Daniel (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | '''Карманная сортировка''' (Bucket sort) | + | '''Карманная сортировка''' (Bucket sort) {{---}} алгоритм сортировки, основанный на предположении о равномерном распределении входных данных. |
== Алгоритм сортировки == | == Алгоритм сортировки == | ||
=== Принцип работы === | === Принцип работы === | ||
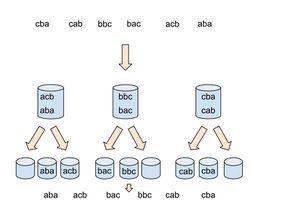
[[Файл:Bucket-sort-example.jpg|right|300px|thumb|Пример работы рекурсивного Bucketsort.]] | [[Файл:Bucket-sort-example.jpg|right|300px|thumb|Пример работы рекурсивного Bucketsort.]] | ||
| − | * элементы массива входных данных разбиваются на <tex>k</tex> блоков ("карманов","корзин"). | + | * элементы массива входных данных разбиваются на <tex>k</tex> блоков ("карманов", "корзин"). |
* каждый из блоков сортируется либо другой сортировкой, либо рекурсивно тем же методом разбиения. | * каждый из блоков сортируется либо другой сортировкой, либо рекурсивно тем же методом разбиения. | ||
* из каждого отсортированного блока данные записываются в массив в порядке разбиения на блоки. | * из каждого отсортированного блока данные записываются в массив в порядке разбиения на блоки. | ||
Важно отметить, что разбиение на блоки производится таким образом, чтобы элементы каждого следующего блока были бы больше предыдущего. | Важно отметить, что разбиение на блоки производится таким образом, чтобы элементы каждого следующего блока были бы больше предыдущего. | ||
=== Реализация === | === Реализация === | ||
| − | Рассмотрим код работы | + | Существует несколько разных реализаций "карманной сортировки". |
| + | ==== Рекурсивный bucket sort ==== | ||
| + | Рассмотрим код работы рекурсивной реализации "карманной сортировки", на вход которой подаются строки длины <tex> p </tex>. | ||
<wikitex> | <wikitex> | ||
| − | Bucketsort ( | + | // j - the current index in string |
| − | if ( | + | //base = 256 |
| − | return | + | Bucketsort (array, j){ |
| − | + | if (array.length < 2 || j == p + 1) | |
| − | + | return array; | |
| − | for i = 0 to | + | initialize buckets <- new array of n empty lists |
| − | + | for i = 0 to array.length - 1 | |
| − | + | insert array[i] at end buckets[partition (array[i], j)] | |
| − | + | for i = 0 to base - 1 | |
| − | for i = 0 to | ||
buckets[i] = Bucketsort (buckets[i],j+1) | buckets[i] = Bucketsort (buckets[i],j+1) | ||
| − | answer | + | intialize answer |
| − | for i = 0 to | + | for i = 0 to base - 1 |
for k = 0 to buckets[i].length - 1 | for k = 0 to buckets[i].length - 1 | ||
| − | + | insert buckets[i][k] аt end answer | |
return answer | return answer | ||
} | } | ||
| + | fuction partition( string s, j) | ||
| + | return int(s[j]) | ||
</wikitex> | </wikitex> | ||
| − | + | base {{---}} основание системы счисления, в случае со строками base <tex> = 256</tex>. | |
| + | ====Не рекурсивная реализация ==== | ||
| + | <wikitex> | ||
| + | function bucketSort(array, n) { | ||
| + | buckets ← new array of n empty lists | ||
| + | for i = 0 to ( array.length - 1) do | ||
| + | insert array[i] into buckets[partition (array[i], k)] | ||
| + | for i = 0 to n - 1 do | ||
| + | nextSort (buckets[i]) | ||
| + | return the concatenation of buckets[0], ..., buckets[ n - 1] | ||
| + | } | ||
| + | </wikitex> | ||
| + | В данном псевдокоде функция partition возвращает для каждого объекта число от <tex>0</tex> до <tex>k - 1</tex>, причем partition монотонная функция. | ||
| + | nextSort {{---}} функция сортирующая массив. | ||
| − | |||
==Асимптотика== | ==Асимптотика== | ||
| − | Пусть <tex>n</tex> - количество элементов в массиве, <tex>k</tex> - основание системы исчисления и | + | Пусть <tex>n</tex> {{---}} количество элементов в массиве, <tex>k</tex> {{---}} основание системы исчисления и |
| − | <tex>p</tex> - количество разрядов в объекте. | + | <tex>p</tex> {{---}} количество разрядов в объекте. |
Тогда алгоритм "Bucket sort" в процессе работы сделает не более чем <Tex>O (p </Tex> <Tex>(n + k))</Tex> итераций. | Тогда алгоритм "Bucket sort" в процессе работы сделает не более чем <Tex>O (p </Tex> <Tex>(n + k))</Tex> итераций. | ||
Заметим, что в случае случайного распределения мат. ожидания количество элементов в каждом блоке <tex> n/k</tex>. Следовательно, в средним алгоритм "карманной сортировки" совершает <Tex>O (n </Tex> <Tex>\log_k n)</Tex> действий. При этом на некотором множестве наборов, где <tex> k = O(n)</tex>, алгоритм отработает за линейное время. | Заметим, что в случае случайного распределения мат. ожидания количество элементов в каждом блоке <tex> n/k</tex>. Следовательно, в средним алгоритм "карманной сортировки" совершает <Tex>O (n </Tex> <Tex>\log_k n)</Tex> действий. При этом на некотором множестве наборов, где <tex> k = O(n)</tex>, алгоритм отработает за линейное время. | ||
| Строка 45: | Строка 60: | ||
* [http://www.google.ru/url?sa=t&rct=j&q=&esrc=s&source=web&cd=10&ved=0CI0BEBYwCQ&url=http%3A%2F%2Fcs.iupui.edu%2F~xkzou%2Fteaching%2FCS580%2FSortinginlineartime.ppt&ei=d7fUT8WWIs3S4QSkkPT-Ag&usg=AFQjCNEUbmlVNhSgrJKV9-QjPBwU6U0obQ&sig2=3yaysrpuwVjmyhjBCpyBeQ Презентация о линейных сортировках]. | * [http://www.google.ru/url?sa=t&rct=j&q=&esrc=s&source=web&cd=10&ved=0CI0BEBYwCQ&url=http%3A%2F%2Fcs.iupui.edu%2F~xkzou%2Fteaching%2FCS580%2FSortinginlineartime.ppt&ei=d7fUT8WWIs3S4QSkkPT-Ag&usg=AFQjCNEUbmlVNhSgrJKV9-QjPBwU6U0obQ&sig2=3yaysrpuwVjmyhjBCpyBeQ Презентация о линейных сортировках]. | ||
| − | + | * [https://www-927.ibm.com/ibm/cas/hspc/student/algorithms/BucketSort.html Приведен код на Jave рекурсивной реализации "карманной" сортировки] | |
| + | * [http://www.youtube.com/watch?v=Iiuqrns0Gwk хорошее обучающее видео по теме bucket sort] | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Сортировки]] | [[Категория: Сортировки]] | ||
Версия 12:02, 11 июня 2012
Карманная сортировка (Bucket sort) — алгоритм сортировки, основанный на предположении о равномерном распределении входных данных.
Содержание
Алгоритм сортировки
Принцип работы
- элементы массива входных данных разбиваются на блоков ("карманов", "корзин").
- каждый из блоков сортируется либо другой сортировкой, либо рекурсивно тем же методом разбиения.
- из каждого отсортированного блока данные записываются в массив в порядке разбиения на блоки.
Важно отметить, что разбиение на блоки производится таким образом, чтобы элементы каждого следующего блока были бы больше предыдущего.
Реализация
Существует несколько разных реализаций "карманной сортировки".
Рекурсивный bucket sort
Рассмотрим код работы рекурсивной реализации "карманной сортировки", на вход которой подаются строки длины . <wikitex>
// j - the current index in string
//base = 256
Bucketsort (array, j){
if (array.length < 2 || j == p + 1)
return array;
initialize buckets <- new array of n empty lists
for i = 0 to array.length - 1
insert array[i] at end buckets[partition (array[i], j)]
for i = 0 to base - 1
buckets[i] = Bucketsort (buckets[i],j+1)
intialize answer
for i = 0 to base - 1
for k = 0 to buckets[i].length - 1
insert buckets[i][k] аt end answer
return answer
}
fuction partition( string s, j)
return int(s[j])
</wikitex> base — основание системы счисления, в случае со строками base .
Не рекурсивная реализация
<wikitex>
function bucketSort(array, n) {
buckets ← new array of n empty lists
for i = 0 to ( array.length - 1) do
insert array[i] into buckets[partition (array[i], k)]
for i = 0 to n - 1 do
nextSort (buckets[i])
return the concatenation of buckets[0], ..., buckets[ n - 1]
}
</wikitex> В данном псевдокоде функция partition возвращает для каждого объекта число от до , причем partition монотонная функция. nextSort — функция сортирующая массив.
Асимптотика
Пусть — количество элементов в массиве, — основание системы исчисления и — количество разрядов в объекте. Тогда алгоритм "Bucket sort" в процессе работы сделает не более чем итераций. Заметим, что в случае случайного распределения мат. ожидания количество элементов в каждом блоке . Следовательно, в средним алгоритм "карманной сортировки" совершает действий. При этом на некотором множестве наборов, где , алгоритм отработает за линейное время. В худшем случае сортировка работает за .
Примечания
Сортировка быстро работает для равновероятного распределения значений разрядов объектов в заданной для них системе счисления. Быстрая сортировка является частным случаем "карманной" сортировки, в случае разбиения всех элементов на "кармана". Также стоит отметить, что по принципу своей работы Bucket sort схожа с Цифровой сортировкой.