Участник:Nechaev/Черновик — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Линейное разрешение коллизий)
 
(не показано 18 промежуточных версий этого же участника)
Строка 1: Строка 1:
−
'''Сортировка подсчётом''' — алгоритм сортировки, в котором используется диапазон чисел сортируемого массива или списка для подсчёта совпадающих элементов. Применение сортировки подсчётом целесообразно лишь тогда, когда сортируемые числа имеют (или их можно отобразить в) диапазон возможных значений, который достаточно мал по сравнению с сортируемым множеством, например, миллион натуральных чисел меньших 1000. Эффективность алгоритма падает, если при попадании нескольких различных элементов в одну ячейку, их надо дополнительно сортировать.  
+
'''Хеш-табли́ца''' {{---}} структура данных, реализующая интерфейс ассоциативного массива. Представляет собой эффективную структуру данных для реализации словарей, а именно, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу.
  
−
== Простой алгоритм ==
+
=== Введение ===
 +
Существует два основных вида хеш-таблиц: ''с цепочками'' и ''открытой адресацией''. Хеш-таблица содержит некоторый массив <tex>H</tex>, элементы которого есть пары (хеш-таблица с открытой адресацией) или списки пар (хеш-таблица с цепочками).
  
−
Это простейший вариант алгоритма. Создать вспомогательный массив <tex>C[0..k - 1]</tex>, состоящий из нулей, затем последовательно прочитать элементы входного массива <tex>A</tex>, для каждого <tex>A[i]</tex> увеличить <tex>C[A[i]]</tex> на единицу. Теперь достаточно пройти по массиву <tex>C</tex>, для каждого <tex>j \in \{0, ..., k - 1\}</tex> в массив <tex>A</tex> последовательно записать число <tex>j</tex> <tex> C[j]</tex> раз.
+
Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Хеш-код <tex>i = h(key)</tex> играет роль индекса в массиве <tex>H</tex>, а зная индекс, мы можем выполнить требующуюся операцию (добавление, удаление или поиск).
−
<code>
 
−
SimpleCountingSort
 
−
    for i = 0 to k - 1
 
−
        C[i] = 0;
 
−
    for i = 0 to n - 1
 
−
        C[A[i]] = C[A[i]] + 1;
 
−
    b = 0;
 
−
    for j = 0 to k - 1
 
−
        for i = 0 to C[j] - 1
 
−
            A[b] = j;
 
−
            b = b + 1;
 
−
</code>
 
  
 +
Количество коллизий зависит от хеш-функции; чем лучше используемая хеш-функция, тем меньше вероятность их возникновения. При вставке в хеш-таблицу размером 365 ячеек всего лишь 23-х элементов вероятность коллизии превышает 50%<ref>
 +
<tex>p(n) = 1 - 1 \cdot \left(1-\frac{1}{len}\right) \cdot \left(1-\frac{2}{len}\right)  \cdots \left(1-\frac{n-1}{len}\right) = { len \cdot len-1 \cdots (len-n+1) \over len^n } </tex> <tex> = { len! \over len^n \cdot (len-n)!},</tex><br>
 +
где <tex>n</tex> {{---}} количество элементов в хеш-таблице, а <tex>len</tex> {{---}} её размер.</ref> (при равномерном распределении значений хеш-функции)<ref>[http://ru.wikipedia.org/wiki/Парадокс_дней_рождения Парадокс дней рождения {{---}} Википедия]</ref>. Способ разрешения коллизий — важная составляющая любой хеш-таблицы.
  
−
== Устойчивый алгоритм ==
+
Полностью избежать коллизий для произвольных данных невозможно в принципе, и хорошая хеш-функция в состоянии только минимизировать их количество. Но, в некоторых специальных случаях их удаётся избежать. Если все ключи элементов известны заранее, либо меняются очень редко, то можно подобрать хеш-функцию, с помощью которой, все ключи будут распределены по хеш-таблице без коллизий. Это хеш-таблицы с ''прямой адресацией''; в них все операции, такие как: поиск, вставка и удаление работают за <tex>O(1)</tex>.
  
−
В этом варианте помимо входного массива <tex>A</tex> потребуется два вспомогательных массива — <tex>C[0..k - 1]</tex> для счётчика и <tex>B[0..n - 1]</tex> для отсортированного массива. Сначала следует заполнить массив <tex>C</tex> нулями, и для каждого <tex>A[i]</tex> увеличить <tex>C[A[i]]</tex> на 1. Далее подсчитывается число элементов меньше или равных текущему. Для этого каждый <tex>C[j]</tex>, начиная с <tex>C[1]</tex>, увеличивают на <tex>C[j - 1]</tex>. На последнем шаге алгоритма читается входной массив с конца, значение <tex>C[A[i]]</tex> уменьшается на 1 и в каждый <tex>B[C[A[i]]]</tex> записывается <tex>A[i]</tex>. Алгоритм устойчив. Устойчивость может потребоваться при [[Сортировка_подсчетом_сложных_объектов|сортировке сложных структур данных]].  
+
Если мы поделим число хранимых элементов на размер массива <tex>H</tex> (число возможных значений хеш-функции), то узнаем коэффициент заполнения хеш-таблицы (англ. ''load factor''). От этого параметра зависит среднее время выполнения операций.
−
<code>
 
−
StableCountingSort
 
−
    for i = 0 to k - 1
 
−
        C[i] = 0;
 
−
    for i = 0 to n - 1
 
−
        C[A[i]] = C[A[i]] + 1;
 
−
    for j = 1 to k - 1
 
−
        C[j] = C[j] + C[j - 1];
 
−
    for i = n - 1 to 0
 
−
        C[A[i]] = C[A[i]] - 1;
 
−
        B[C[A[i]]] = A[i];
 
−
</code>
 
  
−
== Обобщение на произвольный целочисленный диапазон ==
+
=== Хеширование ===
  
−
Если диапазон значений (min и max) заранее не известен, можно воспользоваться линейным поиском min и max, что не повлияет на асимптотику алгоритма. При работе с массивом <tex>C</tex> из <tex>A[i]</tex> необходимо вычитать min, а при обратной записи прибавлять.  
+
'''Хеширование''' {{---}} класс методов поиска, идея которого состоит в вычислении хеш-кода, однозначно определяемого элементом с помощью хеш-функции, и использовании его, как основы для поиска (индексирование в памяти по хеш-коду выполняется за <tex>O(1)</tex>). В общем случае, однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов исходных данных, поэтому существуют элементы, имеющие одинаковые хеш-коды — так называемые коллизии, но если два элемента имеют разный хеш-код, то они гарантированно
 +
различаются. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций.
 +
{{Определение
 +
|id=def1
 +
|definition=<tex>U </tex> {{---}} множество объектов (универсум).<br> <tex>h : U \rightarrow S = \mathcal {f} 0 ... m - 1 \mathcal {g}</tex> {{---}} называется хеш-функцией, где множество <tex>S</tex> хранит ключи из множества <tex>U</tex>.<br> Если <tex>x \in U</tex> значит <tex>h(x) \in S</tex> <br> '''Коллизия:''' <tex>\exists x \neq y : h(x) = h(y)</tex>
 +
}}
 +
==== Виды хеширования ====
 +
* По способу хранения:
 +
** Статическое {{---}} фиксированное количество элементов. Один раз заполняем хеш-таблицу и осуществляем только проверку на наличие в ней нужных элементов.
 +
** Динамическое {{---}} добавляем, удаляем и смотрим на наличие нужных элементов.
 +
* По виду хеш-функции:
 +
** Детерминированная хеш-функция.
 +
** Случайная хеш-функция.
  
−
== Анализ ==
+
=== Свойства хеш-таблицы ===
  
−
В первом алгоритме первые два цикла работают за <tex>\Theta(k)</tex> и <tex>\Theta(n)</tex>, соответственно; двойной цикл за <tex>\Theta(n + k)</tex>. Во втором алгоритме циклы занимают <tex>\Theta(k)</tex>, <tex>\Theta(n)</tex>, <tex>\Theta(k)</tex> и <tex>\Theta(n)</tex>, соответственно. Итого оба алгоритма имеют линейную временную трудоёмкость <tex>\Theta(n + k)</tex>. Используемая память в первом алгоритме равна <tex>\Theta(k)</tex>, а во втором <tex>\Theta(n + k)</tex>.
+
На поиск элемента в хеш-таблице в худшем случае, может потребоваться столько же времени, как и в списке, а именно <tex>\Theta(n)</tex>, но на практике хеширование более эффективно. При некоторых разумных допущениях математическое ожидание времени поиска элемента в хеш-таблице составляет <tex>O(1)</tex>. А все операции (поиск, вставка и удаление элементов) в среднем выполняются за время <tex>O(1)</tex>.
 +
При этом не гарантируется, что время выполнения отдельной операции мало́, так как при достижении некоторого значения коэффициента заполнения необходимо [[Перехеширование. Амортизационный анализ|перехешировать]] таблицу: увеличить размер массива <tex>H</tex> и заново добавить в новую хеш-таблицу все пары.
  
 +
== Разрешение коллизий ==
  
−
== Ссылки ==
+
=== Разрешение коллизий с помощью цепочек ===
 +
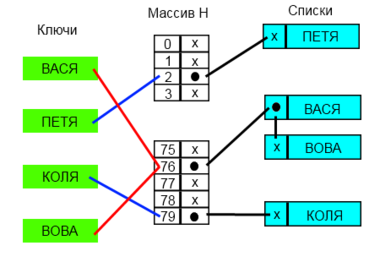
[[Файл:open_hash.png|thumb|380px|right|Разрешение коллизий при помощи цепочек.]]
 +
Каждая ячейка <tex>i</tex> массива <tex>H</tex> содержит указатель на начало списка всех элементов, хеш-код которых равен <tex>i</tex>, либо указывает на их отсутствие. Коллизии приводят к тому, что появляются списки размером больше одного элемента.
  
−
[http://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0_%D0%BF%D0%BE%D0%B4%D1%81%D1%87%D1%91%D1%82%D0%BE%D0%BC Википедия: Сортировка подсчетом]
+
Время, необходимое для вставки в наихудшем случае равно <tex>O(1)</tex>. Это операция выполняет быстро, так как считается, что вставляемый элемент отсутствует в таблице, но если потребуется, то перед вставкой мы можем выполнить поиск этого элемента.
 +
 
 +
Время работы поиска в наихудшем случае пропорционально длине списка, а если все <tex>n</tex> ключей захешировались в одну и ту же ячейку (создав список длиной <tex>n</tex>) время поиска будет равно <tex>\Theta(n)</tex> плюс время вычисления хеш-функции, что ничуть не лучше, чем использование связного списка для хранения всех <tex>n</tex> элементов.
 +
 
 +
Удаления элемента может быть выполнено за <tex>O(1)</tex>, как и вставка, при использовании двухсвязного списка.
 +
 
 +
=== Линейное разрешение коллизий ===
 +
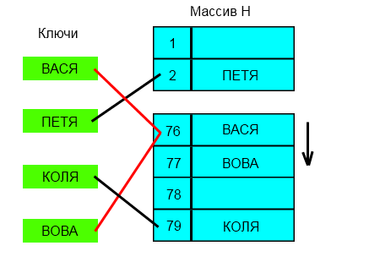
[[Файл:close_hash.png|thumb|380px|right|Пример хеш-таблицы с открытой адресацией и линейным пробированием.]]
 +
Все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличии от хеширования с цепочками, при использовании этого метода может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, следовательно будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.
 +
 
 +
Рассмотрим один из таких методов.<ref>Другой метод борьбы с коллизиями {{---}} [[Двойное хеширование | двойное хеширование]]</ref>
 +
 
 +
В массиве <tex>H</tex> хранятся сами пары ключ-значение. Алгоритм вставки элемента проверяет ячейки массива <tex>H</tex> в заданном порядке до тех пор, пока не будет найдена первая свободная ячейка, в неё и будет записан новый элемент. Это позволяет сэкономить память на хранение указателей.
 +
 
 +
Последовательность, в которой просматриваются ячейки хеш-таблицы, называется последовательностью проб. В общем случае, она зависит только от ключа элемента, то есть это последовательность <tex>h_0(x)</tex>, <tex>h_1(x)</tex>, ...,<tex>h_n</tex><tex>_-</tex><tex>_1</tex><tex>(x)</tex>, где <tex>x</tex> — ключ элемента, а <tex>h_i(x)</tex> — произвольные функции, сопоставляющие каждому ключу ячейку в хеш-таблице. Первый элемент в последовательности, как правило, равен значению некоторой хеш-функции от ключа, а остальные считаются от него каким-нибудь способом. Для успешной работы алгоритмов поиска последовательность проб должна быть такой, чтобы все ячейки хеш-таблицы оказались просмотренными ровно по одному разу.<ref>[[Поиск свободного места при закрытом хешировании | Поиск свободного места при закрытом хешировании]]</ref>
 +
 
 +
== Примечания ==
 +
<references/>
 +
 
 +
== Источники ==
 +
* Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. «Алгоритмы. Построение и анализ» {{---}} «Вильямс», 2011 г. {{---}} 1296 стр. {{---}} ISBN 978-5-8459-0857-5, 5-8459-0857-4, 0-07-013151-1
 +
* Дональд Кнут. «Искусство программирования, том 3. Сортировка и поиск» {{---}} «Вильямс», 2007 г. {{---}} 824 стр. {{---}} ISBN 0-201-89685-0
 +
* [http://ru.wikipedia.org/wiki/Хеш-таблица Хеш-таблица {{---}} Википедия]
 +
 
 +
[[Категория:Дискретная математика и алгоритмы]]
 +
[[Категория:Хеширование]]

Текущая версия на 17:25, 11 июня 2012

Хеш-табли́ца — структура данных, реализующая интерфейс ассоциативного массива. Представляет собой эффективную структуру данных для реализации словарей, а именно, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу.

Введение

Существует два основных вида хеш-таблиц: с цепочками и открытой адресацией. Хеш-таблица содержит некоторый массив [math]H[/math], элементы которого есть пары (хеш-таблица с открытой адресацией) или списки пар (хеш-таблица с цепочками).

Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Хеш-код [math]i = h(key)[/math] играет роль индекса в массиве [math]H[/math], а зная индекс, мы можем выполнить требующуюся операцию (добавление, удаление или поиск).

Количество коллизий зависит от хеш-функции; чем лучше используемая хеш-функция, тем меньше вероятность их возникновения. При вставке в хеш-таблицу размером 365 ячеек всего лишь 23-х элементов вероятность коллизии превышает 50%[1] (при равномерном распределении значений хеш-функции)[2]. Способ разрешения коллизий — важная составляющая любой хеш-таблицы.

Полностью избежать коллизий для произвольных данных невозможно в принципе, и хорошая хеш-функция в состоянии только минимизировать их количество. Но, в некоторых специальных случаях их удаётся избежать. Если все ключи элементов известны заранее, либо меняются очень редко, то можно подобрать хеш-функцию, с помощью которой, все ключи будут распределены по хеш-таблице без коллизий. Это хеш-таблицы с прямой адресацией; в них все операции, такие как: поиск, вставка и удаление работают за [math]O(1)[/math].

Если мы поделим число хранимых элементов на размер массива [math]H[/math] (число возможных значений хеш-функции), то узнаем коэффициент заполнения хеш-таблицы (англ. load factor). От этого параметра зависит среднее время выполнения операций.

Хеширование

Хеширование — класс методов поиска, идея которого состоит в вычислении хеш-кода, однозначно определяемого элементом с помощью хеш-функции, и использовании его, как основы для поиска (индексирование в памяти по хеш-коду выполняется за [math]O(1)[/math]). В общем случае, однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов исходных данных, поэтому существуют элементы, имеющие одинаковые хеш-коды — так называемые коллизии, но если два элемента имеют разный хеш-код, то они гарантированно различаются. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций.

Определение:
[math]U [/math] — множество объектов (универсум).
[math]h : U \rightarrow S = \mathcal {f} 0 ... m - 1 \mathcal {g}[/math] — называется хеш-функцией, где множество [math]S[/math] хранит ключи из множества [math]U[/math].
Если [math]x \in U[/math] значит [math]h(x) \in S[/math]
Коллизия: [math]\exists x \neq y : h(x) = h(y)[/math]

Виды хеширования

  • По способу хранения:
    • Статическое — фиксированное количество элементов. Один раз заполняем хеш-таблицу и осуществляем только проверку на наличие в ней нужных элементов.
    • Динамическое — добавляем, удаляем и смотрим на наличие нужных элементов.
  • По виду хеш-функции:
    • Детерминированная хеш-функция.
    • Случайная хеш-функция.

Свойства хеш-таблицы

На поиск элемента в хеш-таблице в худшем случае, может потребоваться столько же времени, как и в списке, а именно [math]\Theta(n)[/math], но на практике хеширование более эффективно. При некоторых разумных допущениях математическое ожидание времени поиска элемента в хеш-таблице составляет [math]O(1)[/math]. А все операции (поиск, вставка и удаление элементов) в среднем выполняются за время [math]O(1)[/math]. При этом не гарантируется, что время выполнения отдельной операции мало́, так как при достижении некоторого значения коэффициента заполнения необходимо перехешировать таблицу: увеличить размер массива [math]H[/math] и заново добавить в новую хеш-таблицу все пары.

Разрешение коллизий

Разрешение коллизий с помощью цепочек

Разрешение коллизий при помощи цепочек.

Каждая ячейка [math]i[/math] массива [math]H[/math] содержит указатель на начало списка всех элементов, хеш-код которых равен [math]i[/math], либо указывает на их отсутствие. Коллизии приводят к тому, что появляются списки размером больше одного элемента.

Время, необходимое для вставки в наихудшем случае равно [math]O(1)[/math]. Это операция выполняет быстро, так как считается, что вставляемый элемент отсутствует в таблице, но если потребуется, то перед вставкой мы можем выполнить поиск этого элемента.

Время работы поиска в наихудшем случае пропорционально длине списка, а если все [math]n[/math] ключей захешировались в одну и ту же ячейку (создав список длиной [math]n[/math]) время поиска будет равно [math]\Theta(n)[/math] плюс время вычисления хеш-функции, что ничуть не лучше, чем использование связного списка для хранения всех [math]n[/math] элементов.

Удаления элемента может быть выполнено за [math]O(1)[/math], как и вставка, при использовании двухсвязного списка.

Линейное разрешение коллизий

Пример хеш-таблицы с открытой адресацией и линейным пробированием.

Все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличии от хеширования с цепочками, при использовании этого метода может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, следовательно будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.

Рассмотрим один из таких методов.[3]

В массиве [math]H[/math] хранятся сами пары ключ-значение. Алгоритм вставки элемента проверяет ячейки массива [math]H[/math] в заданном порядке до тех пор, пока не будет найдена первая свободная ячейка, в неё и будет записан новый элемент. Это позволяет сэкономить память на хранение указателей.

Последовательность, в которой просматриваются ячейки хеш-таблицы, называется последовательностью проб. В общем случае, она зависит только от ключа элемента, то есть это последовательность [math]h_0(x)[/math], [math]h_1(x)[/math], ...,[math]h_n[/math][math]_-[/math][math]_1[/math][math](x)[/math], где [math]x[/math] — ключ элемента, а [math]h_i(x)[/math] — произвольные функции, сопоставляющие каждому ключу ячейку в хеш-таблице. Первый элемент в последовательности, как правило, равен значению некоторой хеш-функции от ключа, а остальные считаются от него каким-нибудь способом. Для успешной работы алгоритмов поиска последовательность проб должна быть такой, чтобы все ячейки хеш-таблицы оказались просмотренными ровно по одному разу.[4]

Примечания

  1. ↑ [math]p(n) = 1 - 1 \cdot \left(1-\frac{1}{len}\right) \cdot \left(1-\frac{2}{len}\right) \cdots \left(1-\frac{n-1}{len}\right) = { len \cdot len-1 \cdots (len-n+1) \over len^n } [/math] [math] = { len! \over len^n \cdot (len-n)!},[/math]
    где [math]n[/math] — количество элементов в хеш-таблице, а [math]len[/math] — её размер.
  2. ↑ Парадокс дней рождения — Википедия
  3. ↑ Другой метод борьбы с коллизиями — двойное хеширование
  4. ↑ Поиск свободного места при закрытом хешировании

Источники

  • Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. «Алгоритмы. Построение и анализ» — «Вильямс», 2011 г. — 1296 стр. — ISBN 978-5-8459-0857-5, 5-8459-0857-4, 0-07-013151-1
  • Дональд Кнут. «Искусство программирования, том 3. Сортировка и поиск» — «Вильямс», 2007 г. — 824 стр. — ISBN 0-201-89685-0
  • Хеш-таблица — Википедия
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Участник:Nechaev/Черновик&oldid=24953»