Сведение задачи LCA к задаче RMQ — различия между версиями
(→Сложность: fixup) |
(→Препроцессинг: naming and formatting) |
||
| Строка 7: | Строка 7: | ||
== Алгоритм == | == Алгоритм == | ||
=== Препроцессинг === | === Препроцессинг === | ||
| − | + | Для каждой вершины <tex>T</tex> определим глубину вершину с помощью следующей рекурсивной формулы: | |
:<tex>depth(u)= \begin{cases} | :<tex>depth(u)= \begin{cases} | ||
0 & u = root(T),\\ | 0 & u = root(T),\\ | ||
| − | depth(v) + 1 & u = son(v) | + | depth(v) + 1 & u = son(v) |
| − | \end{cases}</tex> | + | \end{cases}.</tex> |
| + | Ясно, что глубина вершины элементарным образом поддерживается во время обхода в глубину. | ||
| − | + | Запустим [[Обход в глубину, цвета вершин|обход в глубину]] из корня, который будет строить список посещений узлов <tex>d</tex>. Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына. | |
=== Запрос === | === Запрос === | ||
Версия 19:33, 12 июня 2012
Содержание
Постановка задачи LCA
| Определение: |
| Наименьшим общим предком (least common ancestor) двух узлов и в корневом дереве называется узел , который среди всех узлов, являющихся предками как узла , так и , имеет наибольшую глубину. |
Пусть дано корневое дерево . На вход подаются запросы вида , для каждого запроса требуется найти их наименьшего общего предка.
Алгоритм
Препроцессинг
Для каждой вершины определим глубину вершину с помощью следующей рекурсивной формулы:
Ясно, что глубина вершины элементарным образом поддерживается во время обхода в глубину.
Запустим обход в глубину из корня, который будет строить список посещений узлов . Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына.
Запрос
Обозначим — функция, возвращающая любой индекс ячейки в списке глубин , в котором хранится глубина узла . Ее можно строить во время обхода в глубину. Пусть имеется запрос — пара узлов В результате обхода в глубину получился список глубин вершин, в котором наименьшему общему предку вершин соответствует минимальная глубина на отрезке .
Доказательство корректности алгоритма
| Теорема: |
Наименьшему общему предку вершин соответствует минимальная глубина на отрезке . |
| Доказательство: |
| Рассмотрим два узла корневого дерева . Рассмотрим отрезок . Поскольку этот отрезок — путь из в , он проходит через их наименьшего общего предка (в дереве есть только один простой путь между вершинами). Покажем, что его глубина минимальна на отрезке . Допустим обратное. Все потомки имеют глубину больше. Но тогда получим, что поиск в глубину вышел из поддерева вершины раньше, чем посетил вершину . |
Пример
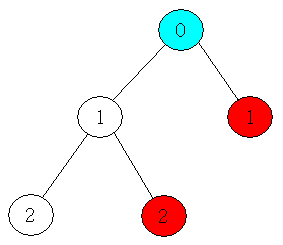
Рассмотрим дерево на рисунке 1. Найдем наименьшего общего предка вершин, помеченных красным цветом. Список глубин, получающийся в результате обхода в глубину - Глубина наименьшего общего предка красных вершин равна минимуму на отрезке
Сложность
Для нахождения минимального элемента на отрезке можно использовать дерево отрезков. Длина массива глубин будет равна , т. е. дерево отрезков можно построить за Таким образом, препроцессинг работает за Время выполнения запроса равно времени запроса минимального элемента на отрезке в дереве отрезков, т. е.
См.также
- Метод двоичного подъема
- Решение RMQ с помощью разреженной таблицы
- Алгоритм Фарака-Колтона и Бендера
- Сведение задачи RMQ к задаче LCA