Сортировка слиянием

Описание

Сортировка слиянием — алгоритм сортировки. Он был пред­ло­жен Джо­ном фон Ней­ма­ном в 1945 го­ду.

Это устойчивый ал­го­ритм, использующий [math]O(n)[/math] дополнительной памяти и [math]O(n[/math] [math]\log(n))[/math] времени.

• Анимированная работа алгоритма (англ.)

Принцип работы

Пример работы процедуры слияния.

Этот алгоритм использует принцип «разделяй и властвуй». Этот принцип заключается в том, что исходная задача разбивается на подзадачи меньшего размера, а потом они решаются рекурсивным методом или же конкретно, если их размер мал. Потом из решения объединяются и получается решение основной (исходной) задачи.

Для процедуры слияния требуется два отсортированных массива. Зная, что массив из одного элемента по определению отсортирован, мы можем разработать такой алгоритм:

1. Массив разбивается на равные (или почти равные) части, до тех пор, пока он не разобьется на части, размер которых равен единице.
2. Далее каждая из частей сортируется по отдельности. Или нет, в случае, если это у нас одиночный элемент.
3. После происходия слияние двух упорядоченных массивов в один.

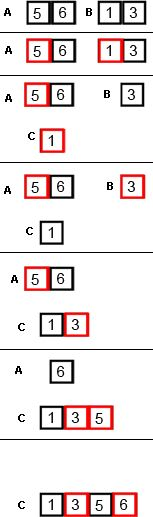
Слияние двух массивов

У нас есть два массива [math]A[/math] и [math]B[/math] (фактически это будут две части одного массива, но для удобства будем писать, что у нас просто два массива). Нам надо получить массив [math]C[/math] размером [math]|A| + |B|[/math]. Для этого можно применить процедуру слияния. Эта процедура заключается в том, что мы сравниваем элементы массивов (начиная с начала) и меньший из них записываем в финальный. И затем, в массиве у которого оказался меньший элемент, переходим к следующему элементу и сравниваем теперь его. В конце, если один из массивов закончился, мы просто дописываем в финальный другой массив. После мы наш финальный массив записываем заместо двух исходных и получаем отсортированный участок.

Ниже приведён псевдокод процедуры слияния, который сливает две части массива A — [left; mid) и [mid; right)

Merge(A, left, mid, right):
  it1 = 0
  it2 = 0
  result = new int[right - left]
  
  while left + it1 < mid and mid + it2 < right:
    if A[left + it1] < A[mid + it2]:
      result[it1 + it2] = A[left + it1]
      it1 += 1
    else:
      result[it1 + it2] = A[mid + it2]
      it2 += 1
  
  while left + it1 < mid:
    result[it1 + it2] = A[left + it1]
    it1 += 1
  
  while mid + it2 < right:
    result[it1 + it2] = A[mid + it2]
    it2 += 1
  
  for i = 0 to it1 + it2:
    A[left + i] = result[i]

Рекурсивный алгоритм

Пример работы рекурсивного алгоритма сортировки слиянием

Функция сортирует участок массива от элемента с номером left до элемен­та с номером right. Будем реализовывать так, что бы производилась сортировка полуинтервала [left, right)

right и left — правая и левая граница массива, middle — середина.

sort(array a, int left, int right)
  middle = left + (right - left ) / 2;  
  if left >= right    
    return;
  sort(a, left, middle);
  sort (a, middle, right);
  merge(array a, left, middle, right);

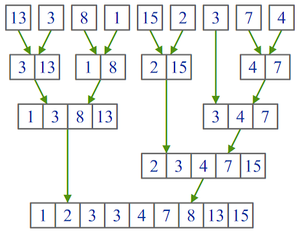
Пример работы алгоритма показан на рисунке:

Время работы

Чтобы оценить время работы этого алгоритма, составим рекуррентное соотношение. Пускай [math]T(n)[/math] — время сортировки массива длины n, тогда для сортировки слиянием справедливо [math]T(n)=2T(n/2)+O(n)[/math]
([math]O(n)[/math] — это время, необходимое на то, чтобы слить два массива). Распишем это соотношение:

[math]T(n)[/math] [math]=[/math] [math]2T(n/2)[/math] [math]+[/math] [math]O(n)[/math] [math]=[/math] [math]4T(n/4)[/math] [math]+[/math] [math]2O(n)[/math] [math]=[/math] [math]...[/math] [math]=[/math] [math]2^kT(1)[/math] [math]+[/math] [math]kO(n).[/math]

Осталось оценить [math]k[/math]. Мы знаем, что [math]2^k=n[/math], а значит [math]k=\log n[/math]. Уравнение примет вид [math]T(n)=nT(1)+ \log n[/math] [math]O(n)[/math]. Так как [math]T(1)[/math] — константа, то [math]T(n)=O(n)+\log n [/math] [math]O(n)=O(n\log n)[/math].

Ссылки

• Википедия — сортировка слиянием
• Сортировка слиянием, анимация и свойства (англ.)
• Примеры реализации на различных языках (Википедия)
• Сортировка слиянием в картинках (источник картинок в статье)