|
|
| Строка 29: |
Строка 29: |
| | }} | | }} |
| | | | |
| − | == Построение дерева за линейное время ==
| |
| − | Пусть дан массив <tex>A[1..N]</tex>. Будем по очереди слева на право добавлять элементы в дерево. Чтобы добавить новое значение <tex>A[i]</tex>, начнем обход из вершины <tex>A[i-1]</tex> к корню, пока не найдем вершину <tex>x</tex>, для которой <tex>x < A[i]</tex>. Тогда правого сына <tex>x</tex> назначим левым сыном <tex>A[i]</tex>, а <tex>A[i]</tex> {{---}} правым сыном <tex>x</tex>. Рассмотрим правую ветку дерева, т.е. по которой проходит обход алгоритма. Заметим, что при добавлении нового узла в дерево элементы, по которым только что прошелся алгоритм отправляются налево, т.е. перестают принадлежать правой ветке. Таким образом процедура поиска родителя не сможет выполнится более <tex>n</tex> раз и итоговая асимптотика алгоритма <tex>O(n)</tex>.
| |
| | == Сложность == | | == Сложность == |
| | Выше описан алгоритм построения дерева за <tex>O(n)</tex>. | | Выше описан алгоритм построения дерева за <tex>O(n)</tex>. |
Версия 14:43, 21 июня 2012
Постановка задачи RMQ
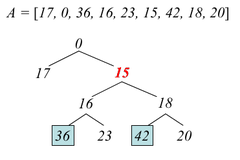
Пример построенного дерева для массива А
Дан массив [math]A[1..N][/math]. Поступают запросы вида [math](i, j)[/math], на каждый запрос требуется найти минимум в массиве [math]A[/math], начиная с позиции [math]i[/math] и заканчивая позицией [math]j[/math].
Алгоритм
Декартово дерево (англ. сartesian tree) по неявному ключу на массиве [math]A[1..N][/math] — это бинарное дерево, допускающее следующее рекурсивное построение:
- Корнем дерева является элемент массива, имеющий минимальное значение [math]A[/math], скажем [math]A[i][/math]. Если минимальных элементов несколько, можно взять любой.
- Левым поддеревом является декартово дерево на массиве [math]A[1..i-1][/math].
- Правым поддеревом является декартово дерево на массиве [math]A[i+1..N][/math].
Здесь и далее [math]A[i][/math] будет также использоваться для обозначения соответствующей вершины дерева.
Построим декартово дерево на массиве [math]A[/math]. Тогда [math]RMQ(i, j)[/math] = [math]LCA(A[i], A[j])[/math].
Доказательство
| Теорема: |
[math]RMQ(i, j)[/math] = [math]LCA(A[i], A[j])[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Положим [math]w = LCA(A[i], A[j])[/math].
Заметим, что [math]A[i][/math] и [math]A[j][/math] не принадлежат одновременно либо правому, либо левому поддереву [math]w[/math], потому как тогда бы соответствующий сын находился на большей глубине, чем [math]w[/math], и также являлся предком как [math]A[i][/math] так и [math]A[j][/math], что противоречит определению [math]LCA[/math]. Из этого замечанию следует, что [math]w[/math] лежит между [math]A[i][/math] и [math]A[j][/math] и, следовательно, принадлежит отрезку [math]A[i..j][/math].
По построению мы также знаем, что:
- Любая вершина дерева имеет свое значение меньшим либо равным значению её детей.
- Поддерево с корнем в [math]w[/math] содержит в себе подмассив [math]A[i..j][/math].
Суммируя, получаем, что [math]w[/math] имеет минимальное значение на отрезке, покрывающем [math]A[i..j][/math], и принадлежит отрезку [math]A[i..j][/math], отсюда [math]RMQ(i, j) = w[/math]. |
| [math]\triangleleft[/math] |
Сложность
Выше описан алгоритм построения дерева за [math]O(n)[/math].
Препроцессинг для [math]LCA[/math] — [math]O(n)[/math] и ответ на запрос [math]O(1)[/math].
В итоге получили [math]RMQ[/math] {построение [math]O(n)[/math], запрос [math]O(1)[/math]}.
См.также
Ссылки
