Дополнительный, самодополнительный граф — различия между версиями
Yurik (обсуждение | вклад) |
Yurik (обсуждение | вклад) |
||
| Строка 10: | Строка 10: | ||
|colspan="2"|Пример графа с 6-ю вершинами и его дополнение. | |colspan="2"|Пример графа с 6-ю вершинами и его дополнение. | ||
|- | |- | ||
| − | | [[Файл:допграф1.png|200px|link= | + | | [[Файл:допграф1.png|200px|link=]] |
| − | | [[Файл:допграф2.png|200px|link= | + | | [[Файл:допграф2.png|200px|link=]] |
|} | |} | ||
| Строка 47: | Строка 47: | ||
Тогда ребро $(u, v) \notin G \Rightarrow (u, v) \in \overline{G} \Rightarrow u$ и $v$ лежат в одной компоненте связности $\overline{G}$. | Тогда ребро $(u, v) \notin G \Rightarrow (u, v) \in \overline{G} \Rightarrow u$ и $v$ лежат в одной компоненте связности $\overline{G}$. | ||
<br> | <br> | ||
| − | [[Файл:допграф3.png|500px|слева | + | [[Файл:допграф3.png|500px|слева]] |
<br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | ||
| Строка 54: | Строка 54: | ||
Тогда по предыдущему пункту $(v, w) \in \overline{G}$ и $(u, w) \in \overline{G} \Rightarrow v$ и $u$ лежат в одной компоненте связности $\overline{G}$. | Тогда по предыдущему пункту $(v, w) \in \overline{G}$ и $(u, w) \in \overline{G} \Rightarrow v$ и $u$ лежат в одной компоненте связности $\overline{G}$. | ||
<br> | <br> | ||
| − | [[Файл:допграф4.png|500px|слева | + | [[Файл:допграф4.png|500px|слева]] |
<br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | ||
| Строка 91: | Строка 91: | ||
Будем доказывать по индукции. Для $k = 1$ утверждение справедливо. | Будем доказывать по индукции. Для $k = 1$ утверждение справедливо. | ||
| − | [[Файл:допграф7.png|400px|link= | + | [[Файл:допграф7.png|400px|link=]] |
Пусть у нас есть самодополнительный граф $G$ с $n$ вершинами, построим самодополнительный граф с $n + 4$ вершинами. | Пусть у нас есть самодополнительный граф $G$ с $n$ вершинами, построим самодополнительный граф с $n + 4$ вершинами. | ||
| Строка 106: | Строка 106: | ||
Тогда между ребрами $A$ и $\overline{A}$ тоже будет биекция. | Тогда между ребрами $A$ и $\overline{A}$ тоже будет биекция. | ||
| − | [[Файл:допграф9.png|400px| | + | [[Файл:допграф9.png|400px|]] |
}} | }} | ||
Версия 21:00, 9 декабря 2012
| НЯ! Эта статья полна любви и обожания. Возможно, стоит добавить ещё больше? |
Дополнительный граф
<wikitex>
| Определение: |
| Пусть дан граф $G<V, E>$. Дополнительным графом к $G$ называется граф $G_1<V, \overline{E}>$, то есть граф с вершинами из $V$ и теми и только теми ребрами из $E$, которые не вошли в $G$. |
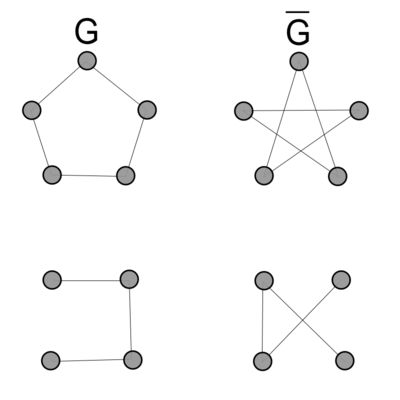
| Пример графа с 6-ю вершинами и его дополнение. | |
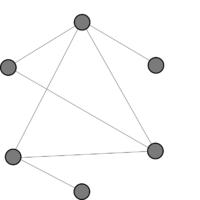
|
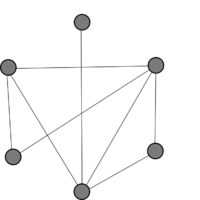
|
| Теорема: |
Дополнительный граф к дополнительному графу $G$ есть граф $G$. |
| Доказательство: |
| $\overline{\overline{G<V, E> |
}}
| Теорема: |
В дополнительном графе к $G<V, E>$ количество ребер равняется . |
| Доказательство: |
| Так как множества ребер в $G$ и $\overline{G}$ дизъюнктны, то $\left\vert E \right\vert + \left\vert \overline{E} \right\vert =$ , из чего следует утверждение теоремы. |
| Теорема: |
Дополнительный граф к несвязному графу связен. |
| Доказательство: |
|
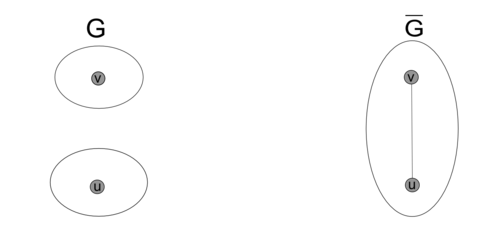
Для графа с одной вершиной утверждение очевидно. Докажем его для остальных графов. Пусть $G$ - данный граф. Рассмотрим произвольные вершины $v$ и $u$ из $G$. Возможны два случая.
Тогда ребро $(u, v) \notin G \Rightarrow (u, v) \in \overline{G} \Rightarrow u$ и $v$ лежат в одной компоненте связности $\overline{G}$.
$G$ — несвязный $\Rightarrow \exists w \in G$, не лежащая в одной компоненте связности с $v$ и $u$.
Тогда по предыдущему пункту $(v, w) \in \overline{G}$ и $(u, w) \in \overline{G} \Rightarrow v$ и $u$ лежат в одной компоненте связности $\overline{G}$.
|
Самодополнительный граф
| Определение: |
| Самодополнительным графом называется граф, изоморфный своему дополнительному. |
| Теорема: |
Любой самодополнительный граф имеет $4k$ или $4k + 1$ вершину. |
| Доказательство: |
|
Обозначим $\left\vert V \right\vert$ за $n$, $\left\vert E \right\vert$ за $a$. Граф самодополнителен $\Rightarrow$ количество его ребер равно количеству ребер в его дополнении. Но по одной из предыдущих теорем, $- a = \left\vert \overline{E} \right\vert = a \Rightarrow 4a = n \cdot \left ( n - 1 \right )$, из чего следует утверждение теоремы. |
</wikitex>
Источники
- Ф. Харари Теория графов, М:Мир 1973г, 29 стр.