Избыточное кодирование, код Хэмминга

Избыточное кодирование - вид кодирования, использующий избыточное количество информации с целью последующего контроля целостности данных при записи/воспроизведении информации или при её передаче по линиям связи.

Код, определяющий одну ошибку

Увеличив объем кода на 1 бит, можно получить возможность определять при передаче наличие одной ошибки. Для этого к коду нужно добавить бит [math]x[/math]: [math]0110..10x[/math], такой, чтобы сумма всех единиц была четной. В случае, если контрольная сумма окажется нечетной, следует отправить запрос на повторную посылку элемента, в котором была обнаружена ошибка. Такое кодирование применяется только если вероятность ошибки крайне мала, например, в оперативной памяти компьютера.

Кодирование Хэмминга

Кодирование Хэмминга предусматривает как возможность обнаружения ошибки, так и возможность её исправления. Рассмотрим простой пример [math]-[/math] закодируем четыре бита: [math]a, b, c, d[/math]. Полученный код будет иметь длину 8 бит и выглядеть следующим образом: [math]a,b,c,d, a \oplus b, c \oplus d, a \oplus c, b \oplus d.[/math] Рассмотрим табличную визуализацию кода:

[math]a[/math]	[math]b[/math]	[math]a \oplus b[/math]
[math]c[/math]	[math]d[/math]	[math]c \oplus d[/math]
[math]a \oplus c[/math]	[math]b \oplus d[/math]

Как видно из таблицы, даже если один из битов [math]a, b, c, d[/math] передался с ошибкой, содержащие его [math]xor[/math]-суммы не сойдутся. Итого, зная строку и столбец в проиллюстрированной таблице можно точно исправить ошибочный бит.

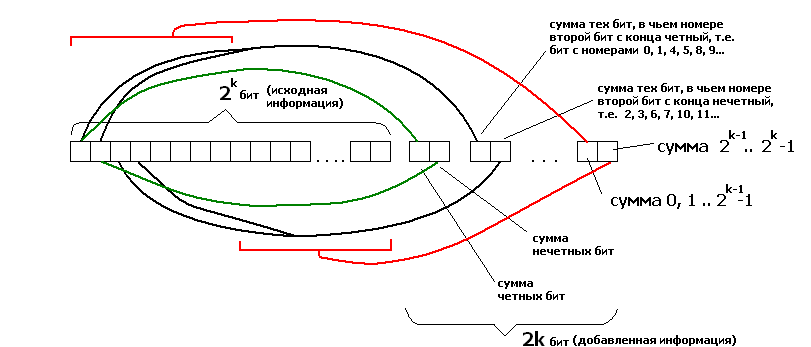
По аналогичному принципу можно закодировать любое число бит. Пусть мы имеем исходную строку длиной в [math]2^k[/math] бит. Для получения её кода добавим к ней [math]k[/math] пар бит по следующему принципу:

• Первая пара: сумма четных бит и сумма нечетных бит
• Вторая пара: сумма тех бит, в чьем номере второй бит с конца ноль и сумма тех бит, в чьем номере второй бит с конца единица

...

• [math]k[/math]-тая пара: сумма тех бит, в чьем номере [math]k[/math]-тый бит с конца ноль и сумма тех бит, в чьем номере [math]k[/math]-тый бит с конца единица
  

Легко понять, что если в одном бите из строки допущена ошибка, то с помощью дописанных [math]k[/math] пар бит можно точно определить, какой именно бит ошибочный. Это объясняется тем, что каждая пара определяет один бит номера ошибочного бита в строке. Всего пар [math]k[/math], следовательно мы имеем [math]k[/math] бит номера ошибочного бита, что вполне достаточно: общее число бит строки не превосходит [math]2^k[/math].

Теперь заметим, что в случае наличия ошибки в исходной строке, ровно один бит в каждой паре будет равен единице. Тогда нам достаточно хранить только один бит из пары, при этом потребуется добавить ещё бит, отвечающий за местонахождение ошибки - в исходной или добавленной части, пусть он будет равен [math]xor[/math]'у всех исходных битов (заметим, что в этом случае этот бит [math]\oplus[/math] бит из пары = второй бит из пары, потому вторые биты в парах не нужны).

Определение и устранение ошибок в общем случае

Пусть [math]\Sigma[/math] — исходный алфавит, [math]C: \Sigma \to B^m[/math] — кодирование, [math]B=(0,1)[/math]

[math]d: B^m,B^m \to R^+[/math] — Расстояние Хэмминга между двумя кодами.
Определим [math]d_0 = \min[/math] [math]~d(c(x),c(y))[/math], [math]x,y \in \Sigma[/math], [math]x \ne y[/math]

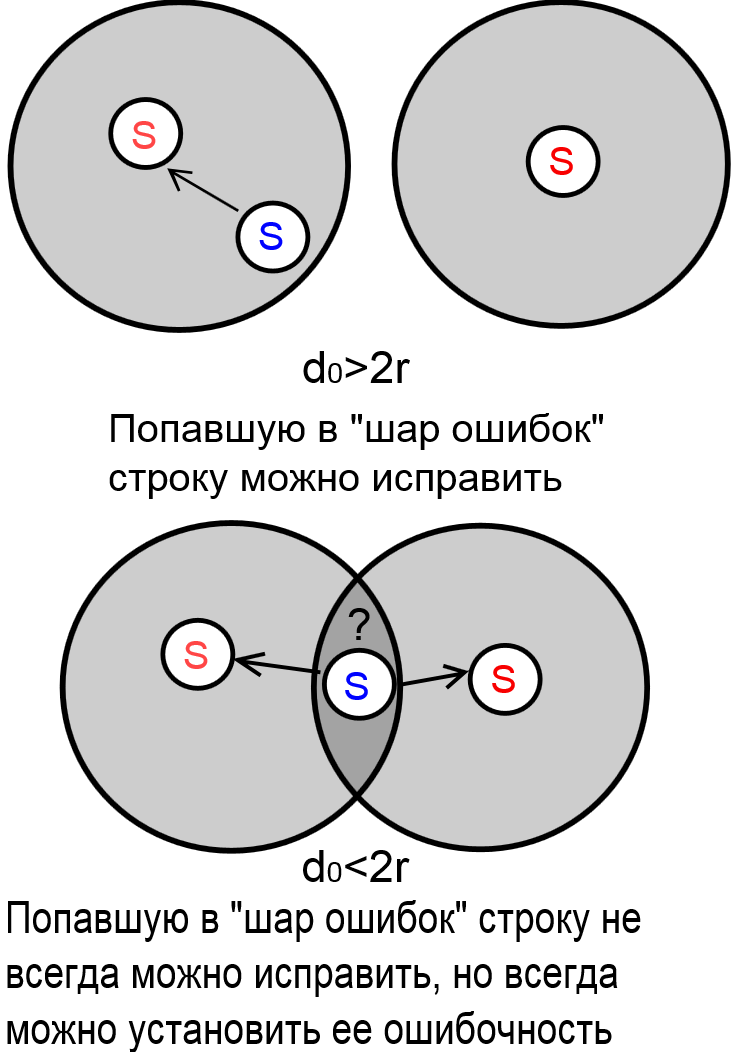
Тогда легко понять, что код, полученный преобразованием [math]C[/math] может исправлять [math]~[[/math][math]{d_0-1}\over{2}[/math][math]~][/math] и обнаруживать [math][d_0-1][/math] ошибок. Действительно, при любом натуральном количестве допустимых ошибок [math]r[/math] любой код [math]S[/math] образует вокруг себя проколотый шар таких строк [math]S_i[/math], что [math]0\lt d(S,S_i)\le r[/math]. Если этот шар не содержит других кодов (что выполняется при [math]r\lt d_0[/math]) , то можно утверждать, что если в него попадает строка, то она ошибочна. Аналогично можно утверждать, что если шары всех кодов не пересекаются (что выполняется при [math]r\le {{d_0-1}\over{2}} [/math]), то попавшую в шар строку [math]S_i[/math] можно считать ошибочной и тождественно исправить на центр шара — строку [math]S[/math].

Ссылки

• Hamming code - Wikipedia, the free encyclopedia