Скрытые Марковские модели — различия между версиями
Gfv (обсуждение | вклад) |
Gfv (обсуждение | вклад) (→Пример) |
||
| Строка 9: | Строка 9: | ||
== Пример == | == Пример == | ||
| − | [[Файл:HMM-Moroz-Example.png|right|Пример СММ]] | + | [[Файл:HMM-Moroz-Example.png|200px|right|Пример СММ]] |
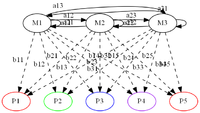
Рассмотрим пример скрытой марковской модели. У Деда Мороза есть три мешка с подарками в разноцветной упаковке: красной, синей, зеленой и фиолетовой. Ночью Дед Мороз пробирается в квартиру и тайком выкладывает подарки под елкой в ряд, доставая по одному подарку из мешка. Наутро мы обнаруживаем упорядоченную последовательность из пяти подарков и хотим сделать наилучшее предположение о последовательности мешков, из которых он доставал эти подарки. | Рассмотрим пример скрытой марковской модели. У Деда Мороза есть три мешка с подарками в разноцветной упаковке: красной, синей, зеленой и фиолетовой. Ночью Дед Мороз пробирается в квартиру и тайком выкладывает подарки под елкой в ряд, доставая по одному подарку из мешка. Наутро мы обнаруживаем упорядоченную последовательность из пяти подарков и хотим сделать наилучшее предположение о последовательности мешков, из которых он доставал эти подарки. | ||
Дед Мороз с мешками {{---}} скрытая марковская модель. При этом 4 цвета {{---}} пространство из <tex>M</tex> возможных событий, 3 мешка {{---}} количество состояний <tex>N</tex>, 5 подарков {{---}} наши <tex>K</tex> наблюдений, каждое из которых представлено цифрой {{---}} номером цвета {{---}} от 1 до 5. Мы знаем, каковы вероятности того, что Дед Мороз начнет доставать подарки из мешка с номером <tex>i</tex> {{---}} вектор <tex>\pi[i]</tex>. Мы также знаем матрицу переходов <tex>A</tex>, какова вероятность того, что от мешка с номером <tex>i</tex> Дед Мороз переходит к мешку с номером <tex>j</tex>. Мешки Деда Мороза бесконечны, но мы точно знаем, каково соотношение цветов подарков в каждом мешке ему загрузили на заводе в Великом Устюге. Это матрица вероятностей эмиссии <tex>B</tex>. | Дед Мороз с мешками {{---}} скрытая марковская модель. При этом 4 цвета {{---}} пространство из <tex>M</tex> возможных событий, 3 мешка {{---}} количество состояний <tex>N</tex>, 5 подарков {{---}} наши <tex>K</tex> наблюдений, каждое из которых представлено цифрой {{---}} номером цвета {{---}} от 1 до 5. Мы знаем, каковы вероятности того, что Дед Мороз начнет доставать подарки из мешка с номером <tex>i</tex> {{---}} вектор <tex>\pi[i]</tex>. Мы также знаем матрицу переходов <tex>A</tex>, какова вероятность того, что от мешка с номером <tex>i</tex> Дед Мороз переходит к мешку с номером <tex>j</tex>. Мешки Деда Мороза бесконечны, но мы точно знаем, каково соотношение цветов подарков в каждом мешке ему загрузили на заводе в Великом Устюге. Это матрица вероятностей эмиссии <tex>B</tex>. | ||
Версия 14:38, 14 января 2013
| Определение: |
| Скрытая Марковская модель — модель процесса, в которой процесс считается Марковским, причем неизвестно, в каком состоянии находится система (состояния скрыты), но каждое состояние может с некоторой вероятностью произвести событие , которое можно наблюдать. |
Модель представляет из себя марковскую цепь, для которой нам известны начальная вероятность и матрица вероятностей переходов. Скрытой она называется потому, что мы не имеем информации о ее текущем состоянии. Мы получаем информацию на основе некоторого наблюдения, в рассмотренном ниже алгоритме мы будем использовать просто натуральное число от 1 до , как индекс наблюдаемого события. Для каждого состояния скрытой марковской модели задан вектор вероятности эмиссии, который характеризует вероятность наблюдения каждого события, когда модель находится в этом состоянии. Совокупность таких векторов образует матрицу эмиссии.
Марковская модель задается как , где — состояния, — возможные события, — начальные вероятности, — матрица переходов, а — вероятность наблюдения события после перехода в состояние .
Пример
Рассмотрим пример скрытой марковской модели. У Деда Мороза есть три мешка с подарками в разноцветной упаковке: красной, синей, зеленой и фиолетовой. Ночью Дед Мороз пробирается в квартиру и тайком выкладывает подарки под елкой в ряд, доставая по одному подарку из мешка. Наутро мы обнаруживаем упорядоченную последовательность из пяти подарков и хотим сделать наилучшее предположение о последовательности мешков, из которых он доставал эти подарки. Дед Мороз с мешками — скрытая марковская модель. При этом 4 цвета — пространство из возможных событий, 3 мешка — количество состояний , 5 подарков — наши наблюдений, каждое из которых представлено цифрой — номером цвета — от 1 до 5. Мы знаем, каковы вероятности того, что Дед Мороз начнет доставать подарки из мешка с номером — вектор . Мы также знаем матрицу переходов , какова вероятность того, что от мешка с номером Дед Мороз переходит к мешку с номером . Мешки Деда Мороза бесконечны, но мы точно знаем, каково соотношение цветов подарков в каждом мешке ему загрузили на заводе в Великом Устюге. Это матрица вероятностей эмиссии .