Парадоксы теории вероятностей

В теории вероятностей существует несколько задач, решение которых, на первый взгляд, противоречит здравому смыслу. Такие задачи называют парадоксами.

Парадокс двух конвертов

Первая формулировка

Есть два неразличимых конверта с деньгами. В обоих конвертах находится некая степень двойки денег, причем в одном находится сумма в два раза большая, чем во втором. Величина этой суммы неизвестна. Конверты дают двум игрокам. Каждый из них может открыть свой конверт и пересчитать в нём деньги. После этого игроки должны решить: стоит ли обменять свой конверт на чужой? Оба игрока рассуждают следующим образом. Я вижу в своём конверте сумму X. Если Х = 1, то менять точно выгодно. если Х другой, то в чужом конверте равновероятно может находиться [math] 2X [/math] или [math] X \over 2[/math]. Поэтому, если я поменяю конверт, то у меня в среднем будет [math] \tfrac{(2X + \tfrac{X}{2})}{2} = \tfrac{5}{4} X [/math], т.е. больше, чем сейчас. Значит обмен выгоден. Однако обмен не может быть выгоден обоим игрокам. Где в их рассуждениях кроется ошибка?

В данном рассуждении ошибка кроется в предположении о том, что в другом конверте может равновероятно находится [math] 2X [/math] или [math] X \over 2[/math]. В действительности этого не может быть.

Предположим от противного, что существует вероятностное распределение [math]p(x)[/math], определенное на степенях двойки так, что [math]p(2^{x_1})[/math] - вероятность того, что в конвертах будут записаны [math]2^{x_1}[/math] и [math]2^{x_1 + 1}[/math], причем значения этой функции на соседних степенях равны. Тогда значения этой функции вообще говоря должны быть равны на всех степенях, т.е. [math]p(x)[/math] постоянна. Но [math]\displaystyle \sum_{i=1}^\infty p(2^i) = 1[/math] (т.к это вероятностное распределение) - противоречие.

Также есть формулировка парадокса, обходящая данное доказательство.

Вторая формулировка

Действительно, пусть нам дано вероятностное распределение геометрической прогрессией:

• вероятность выпадения 1 и 2 в конвертах — [math](1-q)[/math]

• вероятность выпадения 2 и 4 в конвертах — [math](1-q)q[/math]

• вероятность выпадения 4 и 8 в конвертах — [math](1-q)q^2[/math]

• вероятность выпадения [math]2^i[/math] и [math]2^{i+1}[/math] в конвертах — [math](1-q)q^i[/math]

• и так далее.

тогда сумма всех вероятностей действительно [math](1-q) \cdot \frac{1}{(1-q)} = 1[/math]

Итак, пусть нам дали конверт с суммой [math]2^i[/math]. тогда вероятность того, что в другом конверте [math]2^{i-1} \ [/math] — [math] \ \frac{1}{(1+q)} [/math], а того, что в другом конверте [math]2^{i+1} \ [/math] — [math] \ \frac{q}{(1+q)} [/math]

Тогда "в среднем" при обмене мы будем получать [math]\left ( 2^{i-1} \cdot \frac{1}{(1+q)} + 2^{i+1} \cdot \frac{q}{(1+q)} \right ) = 2^i \cdot \left ( \frac{1 + 4q}{2 + 2q} \right ) [/math].

При [math]q \gt \frac{1}{2}[/math] последняя скобка больше единицы. Таким образом "в среднем" мы получим больше, чем [math]2^i[/math]. Такое же рассуждение справедливо для обоих игроков. В чем же тут ошибка рассуждения?

А между тем ошибка тут психологическая. Ведь что человек понимает под понятием "в среднем"? Это некоторое "среднее значение", при условии, что число экспериментов очень велико. Рассчитаем математическое ожидание выигрыша, если мы не будем менять конверты.

[math]E = \displaystyle \frac{(1 - q)}{2} \cdot 1 + \sum_{i=1}^{\infty} \left ( 2^i \cdot \frac{ (1 - q)q^{i-1} + (1-q)q^i }{2} \right ) = \frac{(1 - q)}{2} + (1 - q^2) \sum_{i=0}^{\infty} \left ( 2q \right )^i[/math], а так как [math]q \gt \frac{1}{2}[/math], то под знаком суммирования стоит возрастающая геометрическая прогрессия, тогда [math]E = \infty[/math].

А в равенстве [math] \infty = \infty \cdot \left ( \frac{1 + 4q}{2 + 2q} \right ) [/math] ошибки нет.

Парадокс Монти Холла

Формулировка

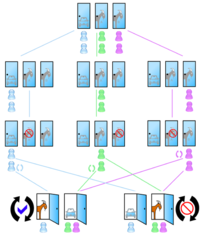
Допустим, вы участвуете в игре. Перед вами три двери, за одной из них - автомобиль, за двумя другими - козы. Вы выбираете одну из трёх дверей и указываете на неё. Ведущий, который знает, за какой дверью машина, открывает одну из двух оставшихся дверей, за которой коза. После этого он предлагает вам выбрать одно из двух: выбрать другую дверь, или не менять свой выбор. Увеличатся ли шансы выиграть авто, если вы выберете другую дверь?

Решение

После того, как ведущий открыл одну из дверей с козой, автомобиль может быть либо за выбранной первоначально дверью, либо за оставшейся. С житейской точки зрения, вероятность выигрыша не зависит от первоначального выбора, при любом поведении одинакова и равна 0,5. Однако, такой ход рассуждений неверен. Предположим, что мы выбрали дверь №1. Пусть событие A - автомобиль за дверью №2. B - автомобиль за дверью №3. [math]P(A) =\frac{2}{3} \cdot \frac{1}{2} = \frac{1}{3}; P(B) = \frac{2}{3} \cdot \frac{1}{2}= \frac{1}{3}[/math], где [math]\frac{1}{2}[/math] - условная вероятность нахождения автомобиля именно за данной дверью при условии, что автомобиль не за дверью, выбранной игроком. Ведущий, открывая одну из оставшихся дверей, всегда проигрышную, сообщает тем самым игроку ровно 1 бит информации и меняет условные вероятности для B и C соответственно на "1" и "0". В результате выражения принимают вид: [math]P(A) = \frac{2}{3} \cdot 1 = \frac{2}{3}[/math]; [math]P(B) = \frac{2}{3} \cdot 0 =0; [/math]

Таким образом, мы видим, что при любом первоначальном выборе, вероятность выиграть, если не менять решения - [math]\frac{1}{3} [/math], а если поменять - [math]\frac{2}{3} [/math], что противоречит интуитивному пониманию данного вопроса. Другими словами, если игрок не меняет решения, то он проиграет в том и только в том случае, если первоначально выбрал дверь за которой автомобиль, а вероятность выбрать автомобиль первоначально составляет [math]\frac{1}{3} [/math].

За выбранной дверью Решение Результат Автомобиль Оставить Выигрыш Коза Оставить Проигрыш Коза Оставить Проигрыш Автомобиль Поменять Проигрыш Коза Поменять Выигрыш Коза Поменять Выигрыш Разбор парадокса Санкт-Петербургский парадокс Иллюстрирует расхождение мат. ожидания выигрыша и его житейской оценки. Формулировка Игроку в казино предлагают сыграть в игру, состоящую в следующем: после уплаты определённого вступительного взноса за участие в игре, игрок подбрасывает честную монету пока у него не выпадет орёл. Если у него выпал орёл с первой попытки, ему выплачивают рубль. Если со второй - два рубля. С третьей - 4, и так далее. После получения денег - игра закончена. Нужно определить, какого размера вступительный взнос должно просить казино, чтобы не остаться в убытке. Разбор Согласно некоторым статистическим данным, игрок готов заплатить за участие в такой игре 10-20, редко 50 рублей, что нелогично с математической точки зрения, ведь мат. ожидание выигрыша в такой ситуации равно бесконечности. Докажем это: Рассмотрим величину [math] E_{n} [/math] - мат. ожидание выигрыша с n-й попытки: [math] E_{1} = 1 \cdot \frac{1}{2} = 0,5[/math]; [math] E_{2} = 2 \cdot \frac{1}{4} = 0,5[/math]; ... [math] E_{n} = \frac{2^{n-1}}{2^n} = 0,5[/math]; Согласно линейности мат. ожидания, мат. ожидание выигрыша в этом случае равно [math]E_{1}+E_{1}+... = 0,5+0,5+0,5 = \infty [/math] Данный парадокс до сих пор не имеет математически полного решения. Нетрудно заметить, что задача легко решается если наложить ограничения на количество игр и предельно малую вероятность, которую можно считать ненулевой. Вероятность того, что в определённой игре количество бросков превысит n, равна [math]\frac{1}{2^{n}}[/math]. Пусть игрок может сыграть не более k игр. Тогда вероятность того, что количество бросков хотя бы в одной игре превысит n, равна [math]1-(1-\frac{1}{2^{n}})^{k}[/math]. Известно, что [math]\lim_{n\rightarrow\infty}1-(1-\frac{1}{2^{n}})^{k} = \frac{k}{2^{n}}[/math] (теорема Бернулли). Пусть p - предельная ненулевая вероятность. Тогда «реальное» количество бросков не превышает [math]\log_2 \frac{k}{p}[/math]. При таком допущении средний выигрыш за одну игру приближёно равен: [math]1 \cdot \frac{1}{2} + 2 \cdot \frac{1}{4}+...+2^{n} \cdot \frac{1}{2^{n+1}}=\frac{n}{2},[/math] где [math]n=\log_2 \frac{k}{p}.[/math] Таким образом, средний выигрыш равен [math]\frac{1}{2} \log_2 \frac{k}{p}.[/math] Ссылки Википедия — Парадокс двух конвертов Википедия — Парадокс Монти Холла Википедия — Санкт-Петербургский парадокс Sinset.com — Парадокс двух конвертов Визуализатор парадокса Монти Холла