Алгоритм Борувки — различия между версиями
(→Реализация) |
Alex z (обсуждение | вклад) |
||
| Строка 58: | Строка 58: | ||
T.addEdge(minEdge[k]) // добавляем ребро если его не было в T | T.addEdge(minEdge[k]) // добавляем ребро если его не было в T | ||
return T; | return T; | ||
| + | |} | ||
| + | |||
| + | ==Пример== | ||
| + | {| class = "wikitable" | ||
| + | ! Изображение !! Множество рёбер !! Описание | ||
| + | |- | ||
| + | |[[Файл:Mst_bor_1.png|200px]] | ||
| + | | | ||
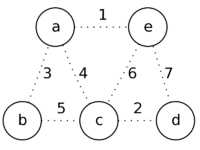
| + | |Переберём все вершины и отметим для каждой вершины инцидентное ей ребро минимального веса. | ||
| + | {| width="100%" | ||
| + | |Вершина || '''a''' || '''b''' || '''c''' || '''d''' || '''e''' | ||
| + | |- | ||
| + | |Ребро минимального веса || '''ae''' || '''ab''' || '''cd''' || '''cd''' || '''ae''' | ||
| + | |} | ||
| + | |- | ||
| + | |[[Файл:Mst_bor_2.png|200px]] | ||
| + | | | ||
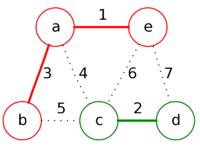
| + | |Объединим каждую полученную компоненту связности в одну вершину.<br/> | ||
| + | Полученные вершины ''abe'' и ''cd'' соединяют рёбра '''bc''', '''ac''', '''ec''' и '''ed'''.<br/> | ||
| + | Выберем среди них ребро с минимальным весом - '''ac''' и положим его между полученными вершинами.<br/> | ||
| + | |- | ||
| + | |[[Файл:Mst_bor_3.png|200px]]<br/>[[Файл:Mst_bor_4.png|200px]] | ||
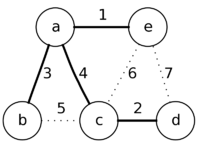
| + | |<center>'''ae''' '''ab''' '''cd'''</center> | ||
| + | |Повторим алгоритм борувки на полученном графе, в результате чего он будет сжат в одну вершину. | ||
| + | |- | ||
| + | |<center>[[Файл:Mst_bor_5.png|80px]]</center> | ||
| + | |<center>'''ae''' '''ab''' '''cd''' '''ac'''</center> | ||
| + | |Граф сжат в одну вершину.<br/>Теперь нужно заменить множество рёбер заданного графа на полученное в алгоритме. | ||
| + | |- | ||
| + | |[[Файл:Mst_bor_6.png|200px]] | ||
| + | | | ||
| + | |Полученный граф - минимальное остовное дерево заданного графа. | ||
|} | |} | ||
| Строка 66: | Строка 98: | ||
Общее время работы алгоритма получается <tex>O(E\log{V})</tex>. | Общее время работы алгоритма получается <tex>O(E\log{V})</tex>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
==См. также== | ==См. также== | ||
* [[Алгоритм Прима]] | * [[Алгоритм Прима]] | ||
* [[Алгоритм Краскала]] | * [[Алгоритм Краскала]] | ||
| + | * [[Алгоритм двух китайцев]] | ||
| + | |||
| + | == Ссылки == | ||
| + | * [http://rain.ifmo.ru/cat/view.php/vis/graph-spanning-trees/mst-2006 Визуализатор алгоритма] | ||
| + | * [http://www.csee.wvu.edu/~ksmani/courses/fa01/random/lecnotes/lecture11.pdf Minimum Spanning Trees] | ||
| + | * [http://ru.wikipedia.org/wiki/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D0%91%D0%BE%D1%80%D1%83%D0%B2%D0%BA%D0%B8 Алгоритм Борувки— Википедия] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Остовные деревья ]] | [[Категория: Остовные деревья ]] | ||
Версия 19:33, 17 января 2013
Алгоритм Борувки — алгоритм поиска минимального остовного дерева (minimum spanning tree, MST) во взвешенном неориентированном связном графе. Впервые был опубликован в 1926 году Отакаром Борувкой.
Содержание
Описание алгоритма
Пусть подграф графа . Изначально содержит все вершины из и не содержит ребер.
Будем добавлять в ребра следующим образом:
Пока не является деревом
- Для каждой компоненты связности находим минимальное по весу ребро, которое связывает вершину из данной компоненты с вершиной, не принадлежащей данной компоненте.
- Добавим в все ребра, которые хотя бы для одной компоненты связности оказались минимальными.
Получившийся граф является минимальным остовным деревом графа .
Данный алгоритм может работать неправильно, если в графе есть ребра равные по весу. Например, полный граф из трех вершин, вес каждого ребра равен один. В могут быть добавлены все три ребра. Избежать эту проблему можно, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером.
Доказательство будем проводить, считая веса всех ребер различными.
Доказательство корректности
| Лемма: |
Рассмотрим связный неориентированный взвешенный граф с инъективной весовой функцией .
Тогда после первой итерации главного цикла алгоритма Борувки получившийся подграф можно достроить до MST. |
| Доказательство: |
| Предположим обратное: пусть любое MST графа не содержит . Рассмотрим какое-нибудь MST. Тогда существует ребро из такое что не принадлежит MST. Добавив ребро в MST, получаем цикл в котором не максимально, т.к оно было минимальным. Тогда, исходя из критерия Тарьяна, получаем противоречие. |
| Теорема: |
Алгоритм Борувки строит MST. |
| Доказательство: |
|
Очевидно, что алгоритм Борувки строит дерево.Будем доказывать что после каждой итерации главного цикла в алгоритме Борувки текущий подграф можно достроить до MST. Докажем это по индукции.
|
Реализация
У вершины есть поле comp — компонента связности, которой принадлежит эта вершина.
Graph Boruvka(Graph G)
while T.size < n - 1
init() // для каждой компоненты связности вес минимального ребра = Inf
findComp(T) // разбиваеv граф T на компоненты связности обычным dfs-ом
for uv E
if u.comp != v.comp
if minEdge[u.comp].w < uv.w
minEdge[u.comp] = uv
if minEdge[v.comp].w < uv.w
minEdge[v.comp] = uv
for k Component // Component — множество компонент связности в T
T.addEdge(minEdge[k]) // добавляем ребро если его не было в T
return T;
|
Пример
Асимптотика
Время работы внутри главного цикла будет равно .
Количество итераций, которое выполняется главным циклом равно так как на каждой итерации количество компонент связности уменьшается в 2 раза (изначально количество компонент равно , в итоге должна стать одна компонента).
Общее время работы алгоритма получается .