Очередь

Определение

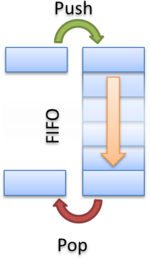
Очередь (Queue)  — это структура данных, добавление и удаление элементов в которой происходит путём операций Push и Pop соответственно. Притом первым из очереди удаляется элемент, который был помещен туда первым, то есть в очереди реализуется принцип «первым вошел — первым вышел» (first-in, first-out — FIFO). У очереди имеется голова (head) и хвост (tail). Когда элемент ставится в очередь, он занимает место в её хвосте. Из очереди всегда выводится элемент, который находится в ее голове.

• [math]push[/math] (запись в очередь) - операция вставки нового элемента.
• [math]pop[/math] (снятие с очереди) - операция удаления нового элемента.
• [math]empty[/math] - проверка очереди на наличие в ней элементов

Реализация на массиве

Очередь, способную вместить не более [math]n[/math] элементов, можно реализовать с помощью массива [math]elements[1..n][/math]. Она будет обладать следующими полями:

• [math]head[/math] (голова очереди)
• [math]tail[/math] (хвост очереди)
• [math]size[/math] (размер очереди)

push

push(x)
   elements[tail] = x
   tail = (tail + 1) % elements.length
   size++

pop

pop()
   if !empty()
      x = elements[head]
      head = (head + 1) % elements.length
      size--
      return x

empty

empty()
   return size == 0

Из-за того что нам не нужно перевыделять память, каждая операция выполняется за [math]O(1)[/math] времени.

Плюсы:

- прост в разработке

- по сравнению с реализацией на списке, есть незначительная экономия памяти

Минусы:

- количество элементов в очереди ограничено размером массива (исправляется написанием функции расширения массива)

- при переполнении очереди требуется перевыделение памяти и копирование всех элементов в новый массив

Реализация на списке

Для данной реализации очереди необходимо создать список ([math]list[/math]) и операции работы на созданном списке.

Реализация очереди на односвязном списке:

list

• [math]x.value[/math] - поле, в котором хранится значение элемента
• [math]x.next[/math] - указатель на следующий элемент очереди

push

push(x)
   element = tail
   tail = new list(x, NULL)
   if size == 0
      head = tail
   else 
      element.next = tail
   size++

pop

pop()
   if empty()
      return
   element = head
   head = head.next
   size--
   return element

empty

empty()
   return size == 0

Каждая операция выполняется за время [math]O(1)[/math].

Минусы:

• Память фрагментируется гораздо сильнее и последовательная итерация по такой очереди может быть ощутимо медленнее, нежели итерация по очереди реализованной на массиве

Реализация на двух стеках

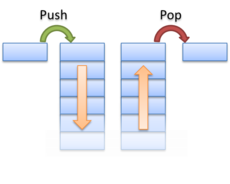
Очередь можно реализовать на двух стеках [math]leftStack[/math] и [math]rightStack[/math]. Один из стеков [math](leftStack)[/math] будем использовать для операции [math]push[/math], другой для операции [math]pop[/math]. При этом, если при попытке извлечения элемента из [math]rightStack[/math] он оказался пустым, просто перенесем все элементы из [math]leftStack[/math] в него (при этом элементы в [math]rightStack[/math] получатся уже в обратном порядке, что нам и нужно для извлечения элементов, а [math]leftStack[/math] станет пустым).

• [math]pushLeft[/math] и [math]pushRight[/math] - функции, реализующие операцию [math]push[/math] для соответствующего стека;
• [math]popLeft[/math] и [math]popRight[/math] - аналогично операции [math]pop[/math].

push

push(x)
   pushLeft(x)

pop

if !rigthStack.empty()
   return popRight()

else
   while !leftStack.empty()
      pushRight(popLeft())
   return popRight()

При выполнении операции [math]push[/math] будем использовать три монеты: одну для самой операции, вторую в качестве резерва на операцию [math]pop[/math] из первого стека, третью во второй стек на финальный [math]pop[/math]. Тогда для операций [math]pop[/math] учётную стоимость можно принять равной нулю и использовать для операции монеты, оставшиеся после операции [math]push[/math].

Таким образом, для каждой операции требуется [math]O(1)[/math] монет, а значит, амортизационная стоимость операций [math]O(1)[/math].

Минусы:

• Если [math]leftStack[/math] не пуст, то операция [math]pop[/math] может выполняться [math]O(n)[/math] времени, в отличии от других реализаций, где [math]pop[/math] всегда выполняется за [math]O(1)[/math]

Реализация на шести стеках

Одним из минусов реализации на двух стеках является то, что в худшем случае мы тратим [math]O(n)[/math] времени на операцию. Если распределить время, необходимое для перемещения элементов из одного стека в другой, по операциям, мы получим очередь без худших случаев с [math]O(1)[/math] истинного времени на операцию.

Сначала будем действовать аналогично случаю с двумя стеками. Пусть у нас есть стек [math]L[/math] для операций [math]push[/math] и стек [math]R[/math] для операций [math]pop[/math]. К моменту опустошения стека [math]R[/math] нам нужно успеть получить стек [math]R'[/math], содержащий текущие элементы стека [math]L[/math] в правильном для извлечения порядке. Перекопирование начнется, когда появится опасность того, что мы не сможем за оставшиеся [math]R.size[/math] операций [math]pop[/math] со стеком [math]R[/math] перекопировать стек [math]L[/math] в новый стек [math]R'[/math]. Очевидно, это ситуация [math]L.size\gt R.size[/math], пусть такое состояние отражает специальная переменная логического типа [math]recopy[/math].

Понятно, что во время перекопирования могут поступить операции [math]push[/math], а стек [math]L[/math] в это время потеряет свою структуру, сложить элементы туда мы уже не сможем, значит нужно завести еще один стек [math]L'[/math], в который мы и будем складывать новые элементы. После окончания перекопирования мы поменяем ролями [math]L,L'[/math] и [math]R,R'[/math], и вроде бы все станет хорошо.

Однако, если реализовать этот алгоритм, мы получим неприятную вещь: старый стек [math]R[/math] может и не опустошиться за это время, то есть мы получили два стека с выходными данными, а значит возможен случай (например, когда все поступающие операции [math]push[/math]), когда при следующем перекопировании у нас не будет свободного стека для копировании туда элементов [math]L[/math]. Для преодоления этой проблемы мы принудительно будем извлекать все элементы из стека [math]R[/math] во вспомогательный стек [math]T[/math], затем копировать элементы из стека [math]L[/math] в [math]R[/math], а затем обратно копировать элементы из стека [math]T[/math] в [math]R[/math]. Легко показать, что приведенный алгоритм как раз получает на выходе в [math]R[/math] все элементы стеков [math]L,R[/math] в правильном порядке.

Но этого еще недостаточно. Если мы принудительно извлекаем элементы из стека [math]R[/math], появляются следующие проблемы:

1. Что вернуть при операции [math]pop[/math]? Для этого заведем себе стек [math]Rc[/math] — копию стека [math]R[/math].
2. Как поддерживать корректность такой копии? Поскольку этот стек нужен только для перекопирования, а во время него он занят, нужна запасная копия [math]Rc'[/math], в которую мы будем копировать все те же элементы, которые мы копируем в [math]R[/math], а по окончании перекопирования поменяем ролями стеки [math]Rc,Rc'[/math], как мы делали со стеками [math]L, L'[/math].

№ Как учесть, что во время перекопирования часть элементов была извлечена из [math]Rc[/math]? Для этого заведем специальную переменную [math]toCopy[/math], которая показывает, сколько корректных элементов находится в стеке [math]T[/math] и уменьшается при каждом извлечении из [math]T[/math] или операции [math]pop[/math]. К счастью, все некорректные элементы будут нарастать с дна стека, так что мы никогда не извлечем некорректный элемент, если [math]toCopy\gt 0[/math].

Если мы использовали стек [math]L[/math] для операций [math]push[/math] и стек [math]R[/math] для операций [math]pop[/math], то для перекопирования мы должны заменить текущий стек [math]R[/math] на новый стек [math]R'[/math], который содержит сначала все элементы [math]L[/math] в обратном порядке, а затем все элементы [math]R[/math] в прямом порядке. Этого можно добиться, если сначала извлечь все элементы [math]R[/math] во вспомогательный стек [math]T[/math], затем извлечь все элементы [math]L[/math] в стек [math]R[/math], а затем обратно извлечь весь стек [math]T[/math] в [math]R[/math]. Поскольку мы выполняем эти действия не сразу, а во время выполнения обычных операций с очередью, нам нужно уметь обрабатывать операции [math]push[/math], для этого будем класть поступающие элементы во вспомогательный стек [math]L'[/math], а для операций [math]pop[/math] будем использовать не стек [math]R[/math], который во время перекопирования потерял свою структуру, а его копию [math]Rc[/math], остающуюся неизменной во время перекопирования. Чтобы сохранить информацию о том, сколько элементов мы уже извлекли из [math]Rc[/math], будем использовать счетчик [math]toCopy[/math], который показывает, сколько элементов из скопированных в [math]T[/math] из [math]R[/math] действительно находятся в очереди, оставшиеся элементы нужно извлечь без копирования.

Для такой реализации будем использовать стеки [math]L_1, L_2, R, Rc_1, Rc_2, T[/math], причем стеки [math]L_1, L_2[/math] используются для операций [math]push[/math], стек [math]R[/math] используется для операций [math]pop[/math], стеки [math]Rc_1, Rc_2[/math] используются в качестве копий стека [math]R[/math] для операций [math]pop[/math] при перекопировании, стек [math]T[/math] используется как временное хранилище элементов [math]R[/math].

В каждый момент времени в очереди зафиксировано, какой [math]L[/math] из стеков [math]L_1[/math] и [math]L_2[/math] используется для помещения туда элементов, пришедших с операцией [math]push[/math], а также какой [math]Rc[/math] из стеков [math]Rc_1[/math] и [math]Rc_2[/math] является в данный момент точной копией стека [math]R[/math].

Также очередь будет запоминать, находится ли она сейчас в режиме перекопирования (recopy mode), в который переходит из обычного режима, когда после очередной операции в стеке [math]L[/math] становится больше элементов, чем в стеке [math]R[/math]. При активации инициализируется счетчик [math]toCopy[/math], показывающий, сколько находится неизвлеченных элементов в стеке [math]Rc[/math].

Обрабатываем поступающие дальше операции следующим образом: [math]push[/math] кладет элемент в парный нашему стеку [math]L[/math] стек [math]L'[/math], а [math]pop[/math] извлекает элемент только из [math]Rc[/math], при этом уменьшая счетчик [math]toCopy[/math]. [math]empty[/math] в этом режиме всегда возвращает [math]false[/math], так как при перекопировании [math]n+1\gt 0[/math] элементов из [math]L[/math] всегда остаются в очереди, так как извлечение происходит только из [math]Rc[/math].

Пусть в этот момент в стеке [math]R[/math], а значит, и в стеке [math]Rc[/math] находились [math]n[/math] элементов, тогда в стеке [math]L[/math] их [math]n+1[/math]. Заметим, что мы можем корректно обработать все операции [math]push[/math] и первые [math]n[/math] операций [math]pop[/math], то есть у нас есть на перекопирование не меньше [math]n+1[/math] операции вместе с активирующей.

Корректной ситуация станет, когда в стеках [math]R[/math] и парном стеке [math]Rc'[/math] окажутся все находящиеся на момент активации в очереди и не извлеченные после активации элементы, причем в порядке, правильном для извлечения.

Чтобы получить корректную ситуацию и перейти в обычный режим, нужно:

1. Извлечь весь стек [math]R[/math] в стек [math]T[/math], [math]n[/math] действий.
2. Извлечь весь стек [math]L[/math] в стеки [math]R, Rc'[/math], [math]n+1[/math] действие.
3. Извлечь [math]toCopy[/math] элементов [math]T[/math] в стеки [math]R, Rc'[/math], а оставшиеся выкинуть, [math]n[/math] действий.
4. Назначить [math]Rc'[/math] текущей копией стека [math]R[/math], а [math]L'[/math] — текущим стеком для операций [math]push[/math], [math]2[/math] действия.

Таким образом, получили [math]3 \cdot n + 3[/math] действий на [math]n + 1[/math] операций с очередью, то есть выполняя 3 дополнительных действия во время операции мы успеем перекопировать все элементы вовремя. Тогда очередь действительно будет выполнять каждое действие за [math]O(1)[/math] реального времени.

Теперь рассмотрим, какие изменения произошли за время перекопирования. Пусть среди [math]n[/math] следующих за активацией операций у нас [math]x[/math] операций [math]pop[/math] и [math]n-x[/math] операций [math]push[/math]. Тогда в стеке [math]R[/math] оказалось [math]2 \cdot n + 1 - x[/math] элементов, а в новом стеке [math]L[/math] оказалось [math]n - x[/math] элементов. Тогда в стеке [math]R[/math] на [math]n+1[/math] больше элементов, чем в стеке [math]L[/math], а это значит, что до следующего режима перекопирования [math]n + 2[/math] операции, и за это время мы успеем очистить старый стек [math]Rc[/math], в котором находится максимум [math]n[/math] ненужных элементов, просто удаляя при каждой операции в обычном режиме один элемент из [math]Rc[/math], если он непуст.

Заметим, что вышеприведенный алгоритм гарантирует нам, что в обычном режиме в стеке [math]L[/math] находится не больше элементов, чем в [math]R[/math], так что проверка на пустоту очереди при обычном режиме сводится к проверке на пустоту стека [math]R[/math].

Пусть наша очередь [math]Q[/math] имеет стеки [math]L1, L2, R, Rc1, Rc2, T[/math], а также переменные [math]recopy[/math] и [math]toCopy[/math], тогда следующий псевдокод выполняет требуемые операции.

empty

empty()
   return !recopy and R.size == 0

push

push(x)
   if !recopy
      L1.push(x)
      checkRecopy()
   else
      L2.push(x)
      checkNormal()

pop

pop()
   if !recopy
      tmp = R.pop()
      Rc1.pop()
      checkRecopy()
      return tmp
   else
      tmp = Rc1.pop()
      toCopy = toCopy - 1
      checkNormal()
      return tmp

checkRecopy

checkRecopy()
   if Rc2.size > 0
      Rc2.pop()
   recopy = L1.size > R.size
   if recopy
      toCopy = Rc1.size
      additionalOperations()

checkNormal

checkNormal()
   additionalOperations()
   // Если мы не все перекопировали, то у нас не пуст стек T
   recopy = T.size != 0

additionalOperations

additionalOperations()
   // Нам достаточно 3 операций на вызов
   toDo = 3
   // Пытаемся перекопировать R в T
   while toDo > 0 and R.size > 0
      T.push(R.pop())
      toDo = toDo - 1
   // Пытаемся перекопировать L1 в R и Rc2
   while toDo > 0 and L1.size > 0
      x = L1.pop()
      R.push(x)
      Rc2.push(x)
      toDo = toDo - 1
   // Пытаемся перекопировать T в R и Rc2 с учетом toCopy
   while toDo > 0 and T.size > 0
      x = T.pop()
      if toCopy > 0
         R.push(x)
         Rc2.push(x)
         toCopy = toCopy - 1
      toDo = toDo - 1
   // Если все скопировано, то меняем роли L1, L2 и Rc1, Rc2
   if T.size = 0
      swap(L1, L2)
      swap(Rc1, Rc2)

Плюсы:

• [math]O(1)[/math] реального времени на операцию.
• Возможность дальнейшего улучшения до персистентной очереди, если использовать персистентные стеки.

Минусы:

• Больше константа на операции.
• Больше расход памяти.
• Больше сложность реализации.

См. также

• Стек

Ссылки

• Википедия - Очередь (программирование)
• Т. Кормен. «Алгоритмы. Построение и анализ» второе издание, Глава 10.1, стр. 262
• T. H. Cormen. «Introduction to Algorithms» third edition, Chapter 10.1, p. 262
• Hood R., Melville R. Real Time Queue Operations in Pure LISP. — Cornell University, 1980