Timsort

Timsort

Timsort — гибридный алгоритм сортировки, сочетающий сортировку вставками и сортировку слиянием.

Данный алгоритм был изобретен в 2002 году Тимом Петерсом(в честь него и назван). В настоящее время Timsort является стандартным алгоритмом сортировки в Python, OpenJDK 7 и реализован в Android JDK 1.5. Чтобы понять почему — достаточно взглянуть на таблицу из Википедии:

Основная идея алгоритма

[math]*[/math] По специальному алгоритму входной массив разделяется на подмассивы.

[math]*[/math] Каждый подмассив сортируется сортировкой вставками.

[math]*[/math] Отсортированные подмассивы собираются в единый массив с помощью модифицированной сортировки слиянием.

Данный алгоритм основывается на том, что в реальном мире сортируемые массивы данных часто содержат в себе упорядоченные подмассивы. На таких данных Timsort существенно быстрее многих дргугих алгоритмов сортировки.

Алгоритм

Используемые понятия и комментарии

[math]*[/math] [math]n[/math] — размер входного массива.

[math]*[/math] [math]run[/math] — некоторый подмассив во входном массиве, который обязан быть упорядоченным одним из двух способов:

1. строго по убыванию [math] a_{i} \gt a_{i + 1} \gt ... [/math].
2. нестрого по возрастанию [math] a_{i} \le a_{i + 1} \le ... [/math].

[math]*[/math] [math]minrun[/math] — минимальный размер подмассива, описанного в предыдущем пункте.

Алгоритм Timsort состоит из нескольких шагов:

Шаг №1. Вычисление minrun

Число [math]minrun[/math] определяется на основе [math] n [/math], исходя из принципов:

[math] * [/math] Оно не должно быть слишком большим, поскольку к подмассиву размера [math] minrun [/math] будет в дальнейшем применена сортировка вставками, а она эффективна только на небольших массивах.

[math] * [/math] Оно не должно быть слишком маленьким, так как чем меньше подмассив — тем больше итераций слияния подмассивов придётся выполнить на последнем шаге алгоритма. Оптимальная величина для [math] n / minrun [/math] — степень двойки. Это требование обусловлено тем, что алгоритм слияния подмассивов наиболее эффективно работает на подмассивах примерно равного размера.

[math]*[/math] Согласно авторским экспериментам:

1. При [math] minrun \gt 256 [/math] нарушается пункт [math]1[/math].
2. При [math] minrun \lt 8 [/math] нарушается пункт [math]2[/math].
3. Наиболее эффективные значения [math] minrun [/math] из диапозона [math] (32; 65) [/math].
4. Исключение — если [math] n \lt 64 [/math], тогда [math] n = minrun [/math] и Timsort превращается в сортировку вставками.

Таким образом, алгоритм расчета [math] minrun [/math] не так уж сложен: берем старшие 6 бит числа [math] n [/math] и добавляем единицу, если в оставшихся младших битах есть хотя бы один ненулевой.

 int GetMinrun(int n) {
     int flag = 0;           /* станет 1 если среди сдвинутых битов есть хотя бы 1 ненулевой */
     while (n >= 64) {
         flag |= n & 1;
         n >>= 1;
     }
     return n + flag;
 }

Шаг №2. Разбиения на подмассивы и их сортировка

На данном этапе у нас есть входной массив, его размер [math]n[/math] и вычисленное число [math]minrun[/math]. Алгоритм работы этого шага:

1. Указатель текущего элемента ставится в начало входного массива.
2. Начиная с текущего элемента, идет поиск во входном массиве упорядоченного подмассива [math]run[/math]. По определению, в [math]run[/math] однозначно войдет текущий элемент и следующий за ним. Если получившийся подмассив упорядочен по убыванию — элементы переставляются так, чтобы они шли по возрастанию.
3. Если размер текущего [math]run[/math] меньше [math]minrun[/math], тогда выбираются следующие за найденным подмассивом [math]run[/math] элементы в количестве [math] minrun - size(run) [/math]. Таким образом, на выходе будет получен подмассив размером большим или равный [math]minrun[/math], часть которого (в лучшем случае — он весь) упорядочена.
4. К данному подмассиву применяем сортировка вставками. Так как размер подмассива невелик и часть его уже упорядочена — сортировка работает эффективно.
5. Указатель текущего элемента ставится на следующий за подмассивом элемент.
6. Если конец входного массива не достигнут — переход к пункту 2, иначе — конец данного шага.

Шаг №3. Слияние

Если данные изначального массива достаточно близки к случайным, то размер упорядоченных подмассивов близок к [math]minrun[/math]. Если в изначальных данных были упорядоченные диапазоны, то упорядоченные подмассивы могут иметь размер, превышающий [math]minrun[/math].

[math]*[/math] Итак, нужно объединить полученные подмассивы для получения результирующего упорядоченного массива. Для достижения эффективности, объединение должно удовлетворять требованиям:

1. Объединять подмассивы примерно равного размера
2. Сохранить стабильность алгоритма (не делать бессмысленных перестановок).
   

Алгоритм шага №3:

1. Создается пустой стек пар <индекс начала подмассива> [math]-[/math] <размер подмассива>.
2. Берется первый упорядоченный подмассив.
3. Добавляется в стек пара данных <индекс начала текущего подмассива> [math]-[/math] <его размер>.
4. При выполнении двух последующих правил выполняется процедура слияния текущего подмассива с предыдущими.

Если [math]X, Y, Z[/math] — размеры трёх верхних подмассивов в стеке, то:

1. [math]X \gt Y + Z[/math]
2. [math]Y \gt Z[/math]

Если одно из правил нарушается — массив [math]Y[/math] сливается с меньшим из массивов [math]X[/math], [math]Z[/math]. Процедура повторяется до выполнения обоих правил или полного упорядочивания данных. Если остались не рассмотренные подмассивы, то берется следующий и переходим ко второму пункту. Иначе — конец.

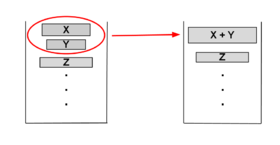
Основная цель этой процедуры — сохранение баланса. Изменения будут выглядеть как на картинке, а значит и размеры подмассивов в стеке эффективны для дальнейшей сортировки слиянием.

Описание процедуры слияния

[math]*[/math] Создается временный массив в размере меньшего из сливаемых подмассивов.

[math]*[/math] Меньший из подмассивов копируется во временный массив

[math]*[/math] Ставятся указатели текущей позиции на первые элементы большего и временного массива.

[math]*[/math] На каждом шаге рассматривается значение текущих элементов в большем и временном массивах, берется меньший из них, копируется в новый отсортированный массив. Указатель текущего элемента перемещается в массиве, из которого был взят элемент.

[math]*[/math] Предыдущий пункт повторяется, пока один из массивов не закончится.

[math]*[/math] Все элементы оставшегося массива добавляются в конец нового массива.

Источники

[math]*[/math] Peter McIlroy "Optimistic Sorting and Information Theoretic Complexity", Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, ISBN 0-89871-313-7, Chapter 53, pp 467-474, January 1993.

[math]*[/math] Magnus Lie Hetland Python Algorithms: Mastering Basic Algorithms in the Python Language. — Apress, 2010. — 336 с.

[math]*[/math] Wikipedia - Timsort

[math]*[/math] Habrahabr - Алгоритм сортировки Timsort