Сверхбыстрый цифровой бор — различия между версиями
Shersh (обсуждение | вклад) |
Shersh (обсуждение | вклад) |
||
| Строка 31: | Строка 31: | ||
===insert=== | ===insert=== | ||
| − | При вставке с помощью succOrPred и двусвязного списка находим следующий и предыдущий элементы и вставляем нужный элемент между ними. А также при создании новой вершины(у которой будет только один ребенок) на обратном пути рекурсии заменяем ссылки. | + | При вставке с помощью <tex>succOrPred</tex> и двусвязного списка находим следующий и предыдущий элементы и вставляем нужный элемент между ними. А также при создании новой вершины (у которой будет только один ребенок) на обратном пути рекурсии заменяем ссылки. |
| − | Удаление происходит аналогично. | + | <code style = "display: inline-block;"> |
| + | // prefixes {{---}} HashMap всех префиксов бора | ||
| + | insert(x) | ||
| + | if prefixes.contains(x): // ''x'' содержится в боре | ||
| + | return | ||
| + | root = insertNode(root, w, x) | ||
| + | Node ''left'' = prec(x), ''right'' = succ(x) | ||
| + | insert ''x'' между ''left'' и ''right'' в двусвязном списке листьев | ||
| + | prefixes.addAll(allPrefixes(x)) | ||
| + | |||
| + | insertNode(vertex, depth, value) | ||
| + | if vertex == <tex> \varnothing </tex>: | ||
| + | vertex = new Node(left = <tex>\varnothing</tex>, right = <tex>\varnothing</tex>, terminal = depth == 0) | ||
| + | if depth == 0: | ||
| + | return vertex | ||
| + | if hiBit(x) == 0: | ||
| + | vertex.left = insertNode(vertex.left, depth - 1, x[1:]) | ||
| + | else: | ||
| + | vertex.right = insertNode(vertex.right, depth - 1, x[1:]) | ||
| + | // ещё вставка min & max | ||
| + | </code> | ||
| + | |||
| + | ===delete=== | ||
| + | Удаление происходит аналогично добавлению. Модифицируем бор, чтобы в вершине был счётчик, сколько у неё вершин в поддереве. Если 0, то удаляем её совсем. Иначе же, если удалился какой-то из сыновей, то надо обновить ссылки min и max. Это сделать просто {{---}} ссылкой на минимум (максимум) в правом (левом) поддереве становится <tex> successor ~(predecessor)</tex> удалённой вершины. | ||
| + | |||
Вставка и удаление выполняются за <tex>O(w)</tex>. | Вставка и удаление выполняются за <tex>O(w)</tex>. | ||
===binarySearch=== | ===binarySearch=== | ||
| − | Пока что мы не добились асимптотического выигрыша - все операции по-прежнему выполняются за <tex>O(w)</tex>. Теперь слабое место - это поиск наибольшего общего префикса. Будем искать его двоичным поиском. Для этого занесём префиксы всех чисел в HashMap - ассоциативный массив, который по префиксу возвращает вершину в боре (чтобы избежать проблемы с ведущими нулями, используем при поиске маску вида <tex>0...01...1</tex> | + | Пока что мы не добились асимптотического выигрыша {{---}} все операции по-прежнему выполняются за <tex>O(w)</tex>. Теперь слабое место {{---}} это поиск наибольшего общего префикса. Будем искать его двоичным поиском. Для этого занесём префиксы всех чисел в <tex> HashMap </tex> {{---}} [[Хеш-таблица |ассоциативный массив]], который по префиксу возвращает вершину в боре <tex>(</tex>чтобы избежать проблемы с ведущими нулями, используем при поиске маску вида <tex>0...01...1)</tex>. Запустим двоичный поиск по длине наибольшего общего префикса. Как только он вернет максимальный префикс, переходим в вершину (у этой вершины не может быть два сына, так как тогда поиск бы не завершился) и там за <tex>O(1)</tex> находим минимум или масимум, и за <tex>O(1)</tex> переходим по списку, если нужно. |
Итого операции <tex>find, succ</tex> и <tex>pred</tex> будут выполняться за <tex>O(\log w)</tex>. | Итого операции <tex>find, succ</tex> и <tex>pred</tex> будут выполняться за <tex>O(\log w)</tex>. | ||
| Строка 46: | Строка 70: | ||
Уменьшим количество занимаемой памяти. | Уменьшим количество занимаемой памяти. | ||
| − | Пусть <tex>a_1 < a_2 < a_3 < ... < a_n</tex> - числа, которые нужно хранить в боре. | + | Пусть <tex>a_1 < a_2 < a_3 < ... < a_n</tex> {{---}} числа, которые нужно хранить в боре. |
| − | Выберем какое-то <tex>k</tex> (что за <tex>k</tex> - будет видно дальше). Разобьём их на <tex>s</tex> блоков размером от <tex>\frac{k}{2}</tex> до <tex>2k</tex>, а точнее <tex>B_{11} < B_{12} < ... < B_{ | + | Выберем какое-то <tex>k</tex> (что за <tex>k</tex> {{---}} будет видно дальше). Разобьём их на <tex>s</tex> блоков размером от <tex dpi=150>\frac{k}{2}</tex> до <tex>2k</tex>, а точнее <tex>B_{11} < B_{12} < ... < B_{1n_{1}} < B_{21} < ... < B_{2n_{2}} < ... < B_{s1} < ... < B_{sn_{s}}</tex> |
| − | Выберем в каждом блоке какого-нибудь представителя. И поместим этих представителей в <tex>x-fast-trie</tex>. Всего в <tex>x-fast-trie</tex> будет <tex>O(\frac{2 \cdot n \cdot w} {k})</tex> элементов. Поэтому если выбрать <tex>k = \Omega(w)</tex>, то <tex>x{-}fast{-}trie</tex> будет занимать <tex>O(n)</tex> памяти. | + | Выберем в каждом блоке какого-нибудь представителя. И поместим этих представителей в <tex>x{-}fast{-}trie</tex>. Всего в <tex>x{-}fast{-}trie</tex> будет <tex dpi=150>O(\frac{2 \cdot n \cdot w} {k})</tex> элементов. Поэтому если выбрать <tex>k = \Omega(w)</tex>, то <tex>x{-}fast{-}trie</tex> будет занимать <tex>O(n)</tex> памяти. |
| − | Каждый лист <tex>x{-}fast{-}trie</tex> является представителем блока, а все остальные элементы блока (в т. ч. и представителя) подвесим к листу как сбалансированное двоичное дерево поиска. В дереве может храниться от <tex>\frac{w}{2}</tex> до <tex>2w</tex> элементов, поэтому его высота - <tex>O(\log w)</tex>. | + | Каждый лист <tex>x{-}fast{-}trie</tex> является представителем блока, а все остальные элементы блока (в т. ч. и представителя) подвесим к листу как сбалансированное двоичное дерево поиска. В дереве может храниться от <tex dpi=150>\frac{w}{2}</tex> до <tex>2w</tex> элементов, поэтому его высота {{---}} <tex>O(\log w)</tex>. |
| − | Все деревья поиска занимают <tex>O(n)</tex> памяти, и <tex>x{-}fast{-}trie | + | Все деревья поиска занимают <tex>O(n)</tex> памяти, и <tex>x{-}fast{-}trie {{---}} O(n)</tex> памяти. Поэтому <tex>y{-}fast{-}trie</tex> тоже занимает <tex>O(n)</tex> памяти. |
===find=== | ===find=== | ||
| − | Находим <tex>succ = x</tex> среди представителей в <tex>x{-}fast{-}trie</tex>, а потом запускаем поиск <tex>succ(x)</tex> в дереве, подвешенном к листу <tex>x</tex>, а также в дереве, подвешенном к листу <tex>pred(x)</tex> среди представителей в <tex>x-fast-trie</tex>. Представителем дерева является необязательно минимальный или максимальный элемент, поэтому нужно запустить в двух деревьях. Заметим, что мы ищем элемент только в двух деревьях, так как искомый элемент точно находится между | + | Находим <tex>succ = x</tex> среди представителей в <tex>x{-}fast{-}trie</tex>, а потом запускаем поиск <tex>succ(x)</tex> в дереве, подвешенном к листу <tex>x</tex>, а также в дереве, подвешенном к листу <tex>pred(x)</tex> среди представителей в <tex>x{-}fast{-}trie</tex>. Представителем дерева является необязательно минимальный или максимальный элемент, поэтому нужно запустить в двух деревьях. Заметим, что мы ищем элемент только в двух деревьях, так как искомый элемент точно находится между своими следующим и предыдущим элементами. |
| − | <tex>O(\log w)</tex> на поиск в <tex>x{-}fast{-}trie</tex> и <tex>O(\log w)</tex> на поиск в деревьях поиска, поэтому итогая асимптотика - <tex>O(\log w)</tex>. | + | <tex>O(\log w)</tex> на поиск в <tex>x{-}fast{-}trie</tex> и <tex>O(\log w)</tex> на поиск в деревьях поиска, поэтому итогая асимптотика {{---}} <tex>O(\log w)</tex>. |
<tex>succ</tex> и <tex>pred</tex> выполняются аналогично. | <tex>succ</tex> и <tex>pred</tex> выполняются аналогично. | ||
===insert=== | ===insert=== | ||
| − | Вставка элемента <tex>x</tex> происходит следующим образом: найдём <tex>succ(x)</tex> и вставим его в подвешенное к листу дерево. Но может возникнуть плохая ситуация: размер дерева станет <tex>2 \cdot w + 1</tex>. Тогда поступим следующим образом | + | Вставка элемента <tex>x</tex> происходит следующим образом: найдём <tex>succ(x)</tex> и вставим его в подвешенное к листу дерево. Но может возникнуть плохая ситуация: размер дерева станет <tex>2 \cdot w + 1</tex>. Тогда поступим следующим образом: удалим наше дерево из <tex>x{-}fast{-}trie</tex>, разделим его на элементы, из которых построим два дерева размером <tex>w</tex> и <tex>w + 1</tex>, и вставим в <tex>x{-}fast{-}trie</tex> их оба. |
===delete=== | ===delete=== | ||
| − | Удаление происходит аналогично, только если размер дерева станет <tex>\frac{w}{2} - 1</tex>, то надо его слить с любым соседним деревом. А если после слияния размер получившегося дерева станет больше <tex>2 \cdot w</tex>, то надо его разделить аналогично предыдущему случаю. | + | Удаление происходит аналогично, только если размер дерева станет <tex dpi=150>\frac{w}{2} - 1</tex>, то надо его слить с любым соседним деревом. А если после слияния размер получившегося дерева станет больше <tex>2 \cdot w</tex>, то надо его разделить аналогично предыдущему случаю. |
| + | |||
| + | [[АВЛ-дерево |АВЛ-деревья]] или [[Красно-черное дерево |красно-чёрные]] позволяют выполнять слияние и разделение за линейное время, поэтому операции вставки и удаления выполняются за <tex>O(w)</tex>. | ||
===Ассимптотика=== | ===Ассимптотика=== | ||
Заметим, что вставка, которая не модифицирует верхний бор, выполняется за истинный <tex>\log w</tex>, также и <tex>succ, pred</tex>. | Заметим, что вставка, которая не модифицирует верхний бор, выполняется за истинный <tex>\log w</tex>, также и <tex>succ, pred</tex>. | ||
| − | Плохие операции | + | Плохие операции {{---}} которые модифицируют верхний бор. Но они не происходят слишком часто. |
| − | Применим амортизационный анализ, используя метод предоплаты. Копим деньги на дешевых операциях. | + | Применим амортизационный анализ, используя метод предоплаты. Копим деньги на дешевых операциях. Слияние массивов осуществляется за <tex>O(w)</tex>, как и разделение. Поэтому если мы накопим <tex>\Omega(w)</tex> дополнительных денег на дешёвых операциях, то сумеем расплатиться за все остальные, просто положив константное число дополнительных монет во время каждой операции. Худший для разделения случай произойдет, если мы дальше будем только добавлять элементы {{---}} было <tex dpi=150>\frac{w}{2} - 1</tex> и <tex>2 \cdot w</tex>, слили, стало больше <tex>2 \cdot w</tex>, разделили, таким образом получили два дерева с <tex dpi=150>\frac{5\cdot w}{4}</tex> элементами. Худший случай для слияния, когда у нас <tex>w</tex> элементов (просиходит после разделения <tex>2 \cdot w + 1</tex> дерева). Заметим, что в каждом случае дерево находится на расстоянии <tex>\Theta(w)</tex> от границ. Следовательно, если мы будем класть определённое константное число монет, то скопим их достаточно, чтобы расплатиться за дорогие операции слияния и разделения деревьев. |
| − | Получаем амортизированную оценку <tex>O(\log w)</tex> и истинную - <tex>O(w)</tex>. | + | Получаем амортизированную оценку <tex>O(\log w)</tex> и истинную {{---}} <tex>O(w)</tex>. |
| − | + | Получилась та же оценка на операции, что и у дерева Ван Эмде Боаса, но структура данных занимает <tex>O(n)</tex> памяти. | |
| − | Получилась та же оценка на операции, что и у | ||
==Ссылки== | ==Ссылки== | ||
| − | *[ | + | *[[wikipedia:Y-fast_trie | Y-fast trie {{---}} Wikipedia]] |
| − | *[ | + | *[[wikipedia:X-fast_trie | X-fast trie {{---}} Wikipedia]] |
*[http://compscicenter.ru/program/lecture/6902 Лекция А. С. Станкевича] | *[http://compscicenter.ru/program/lecture/6902 Лекция А. С. Станкевича] | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Деревья поиска]] | [[Категория: Деревья поиска]] | ||
Версия 04:01, 9 июня 2013
Содержание
Цифровой бор
Работаем с целыми числами, которые представляются с помощью битов, аналогично дереву Ван Эмде Боаса. Мы можем их складывать, вычитать, умножать, сдвигать, производить с ними логические операции, адресоваться ими. В модели памяти , которая сейчас применима к большинству процессоров, эти операции могут быть выполнены за .
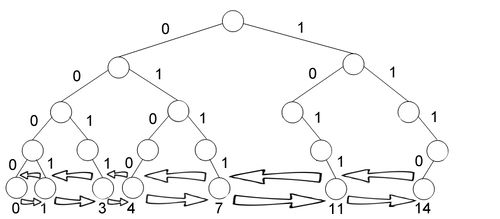
Цифровой бор — бор, в котором в качестве строк используются двоичные записи чисел, включая ведущие нули. Таким образом он имеет глубину .
Цифровой бор поддерживает операции .
Добавление вершины происходит так же, как и в обычном боре. Удаление можно выполнять лениво — просто убирая пометку с листа. А можно хранить число пометок в поддереве и удалять вершину, если это число стало равным нулю.
succ
Поиск следующего элемента осуществляется проходом от корня до вершины, из которой не можем пойти в нужную сторону. Если не смогли пойти влево по ребру , то ответ — минимум в правом поддереве. Если не смогли пойти вправо, поднимаемся наверх, пока являемся правым ребенком; если стали левым, то поднимаемся, пока у вершины нет правого ребенка (если такой ситуации нет, то запрос больше всех элементов). Тогда ответ — минимум в правом поддереве.
Преимущества: простая реализация, занимает памяти, все операции выполняются за .
Хуже дерева Ван Эмде Боаса по скорости, но памяти занимает меньше.
Быстрый цифровой бор (x-fast-trie)
Он по-прежнему будет занимать памяти, но немодифицирующие операции будут выполняться за .
Улучшим структуру: было два слабых места — подниматься вверх и искать минимум.
succOrPred
Первая модификация — занесем все элементы в двусвязный список в порядке, в котором они лежат в боре. Добавим операцию , которая возвращает следующий или предыдущий в зависимости от того, что проще. Работает она так: спускается вниз до наибольшего общего префикса, а потом до минимума в правом дереве или же до максимума в левом. Тогда мы получим какой-то элемент списка и не более чем за два шага в списке сможем получить ответ на запрос.
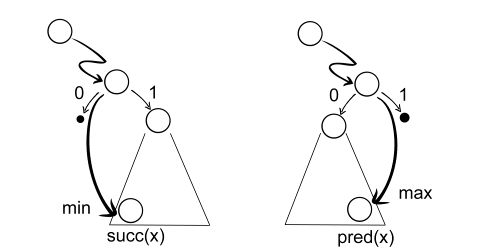
Вторая модификация — добавим ссылки. Операции поиска минимума и максимума дорогие, выполним их за . Теперь становится понятно, что необязательно спускаться до минимума или максимума в дереве. Если у вершину нет левого сына, отметим это одним битом, а вместо ссылки на левого сына сделаем ссылку на минимум в правом поддереве, что удобно для нашей реализации . Если нет правого сына, то храним ссылку на максимум в левом поддереве.
insert
При вставке с помощью и двусвязного списка находим следующий и предыдущий элементы и вставляем нужный элемент между ними. А также при создании новой вершины (у которой будет только один ребенок) на обратном пути рекурсии заменяем ссылки.
// prefixes — HashMap всех префиксов бора
insert(x)
if prefixes.contains(x): // x содержится в боре
return
root = insertNode(root, w, x)
Node left = prec(x), right = succ(x)
insert x между left и right в двусвязном списке листьев
prefixes.addAll(allPrefixes(x))
insertNode(vertex, depth, value) if vertex == : vertex = new Node(left = , right = , terminal = depth == 0) if depth == 0: return vertex if hiBit(x) == 0: vertex.left = insertNode(vertex.left, depth - 1, x[1:]) else: vertex.right = insertNode(vertex.right, depth - 1, x[1:]) // ещё вставка min & max
delete
Удаление происходит аналогично добавлению. Модифицируем бор, чтобы в вершине был счётчик, сколько у неё вершин в поддереве. Если 0, то удаляем её совсем. Иначе же, если удалился какой-то из сыновей, то надо обновить ссылки min и max. Это сделать просто — ссылкой на минимум (максимум) в правом (левом) поддереве становится удалённой вершины.
Вставка и удаление выполняются за .
binarySearch
Пока что мы не добились асимптотического выигрыша — все операции по-прежнему выполняются за . Теперь слабое место — это поиск наибольшего общего префикса. Будем искать его двоичным поиском. Для этого занесём префиксы всех чисел в — ассоциативный массив, который по префиксу возвращает вершину в боре чтобы избежать проблемы с ведущими нулями, используем при поиске маску вида . Запустим двоичный поиск по длине наибольшего общего префикса. Как только он вернет максимальный префикс, переходим в вершину (у этой вершины не может быть два сына, так как тогда поиск бы не завершился) и там за находим минимум или масимум, и за переходим по списку, если нужно.
Итого операции и будут выполняться за .
Сверхбыстрый цифровой бор (y-fast-trie)
Теперь усовершенствуем до , который занимает памяти, а все операции выполняются за , правда, для модифицирующих операций эта оценка будет амортизированной.
Уменьшим количество занимаемой памяти. Пусть — числа, которые нужно хранить в боре. Выберем какое-то (что за — будет видно дальше). Разобьём их на блоков размером от до , а точнее
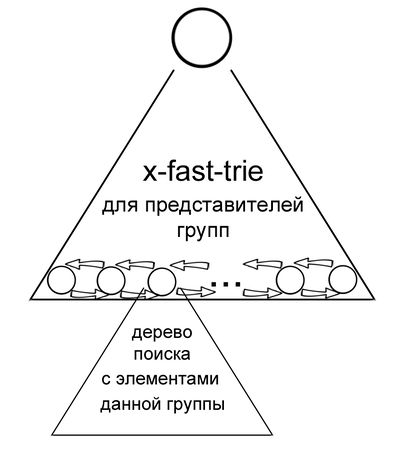
Выберем в каждом блоке какого-нибудь представителя. И поместим этих представителей в . Всего в будет элементов. Поэтому если выбрать , то будет занимать памяти.
Каждый лист является представителем блока, а все остальные элементы блока (в т. ч. и представителя) подвесим к листу как сбалансированное двоичное дерево поиска. В дереве может храниться от до элементов, поэтому его высота — .
Все деревья поиска занимают памяти, и памяти. Поэтому тоже занимает памяти.
find
Находим среди представителей в , а потом запускаем поиск в дереве, подвешенном к листу , а также в дереве, подвешенном к листу среди представителей в . Представителем дерева является необязательно минимальный или максимальный элемент, поэтому нужно запустить в двух деревьях. Заметим, что мы ищем элемент только в двух деревьях, так как искомый элемент точно находится между своими следующим и предыдущим элементами. на поиск в и на поиск в деревьях поиска, поэтому итогая асимптотика — .
и выполняются аналогично.
insert
Вставка элемента происходит следующим образом: найдём и вставим его в подвешенное к листу дерево. Но может возникнуть плохая ситуация: размер дерева станет . Тогда поступим следующим образом: удалим наше дерево из , разделим его на элементы, из которых построим два дерева размером и , и вставим в их оба.
delete
Удаление происходит аналогично, только если размер дерева станет , то надо его слить с любым соседним деревом. А если после слияния размер получившегося дерева станет больше , то надо его разделить аналогично предыдущему случаю.
АВЛ-деревья или красно-чёрные позволяют выполнять слияние и разделение за линейное время, поэтому операции вставки и удаления выполняются за .
Ассимптотика
Заметим, что вставка, которая не модифицирует верхний бор, выполняется за истинный , также и . Плохие операции — которые модифицируют верхний бор. Но они не происходят слишком часто.
Применим амортизационный анализ, используя метод предоплаты. Копим деньги на дешевых операциях. Слияние массивов осуществляется за , как и разделение. Поэтому если мы накопим дополнительных денег на дешёвых операциях, то сумеем расплатиться за все остальные, просто положив константное число дополнительных монет во время каждой операции. Худший для разделения случай произойдет, если мы дальше будем только добавлять элементы — было и , слили, стало больше , разделили, таким образом получили два дерева с элементами. Худший случай для слияния, когда у нас элементов (просиходит после разделения дерева). Заметим, что в каждом случае дерево находится на расстоянии от границ. Следовательно, если мы будем класть определённое константное число монет, то скопим их достаточно, чтобы расплатиться за дорогие операции слияния и разделения деревьев.
Получаем амортизированную оценку и истинную — .
Получилась та же оценка на операции, что и у дерева Ван Эмде Боаса, но структура данных занимает памяти.