Моноид — различия между версиями
(тыц) |
|||
| Строка 18: | Строка 18: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Свободным моноидом''' (англ. ''free monoid'') <tex> M </tex> над множеством <tex> S </tex> <tex>(</tex>обозначается как <tex> M_S )</tex> называется моноид над множеством <tex> S^* </tex> {{---}} набором всевозможных элементов, полученных конечным числом применений ассоциативной операции к элементам | + | '''Свободным моноидом''' (англ. ''free monoid'') <tex> M </tex> над множеством <tex> S </tex> <tex>(</tex>обозначается как <tex> M_S )</tex> называется моноид над множеством <tex> S^* </tex> {{---}} набором всевозможных элементов, полученных конечным числом применений ассоциативной операции к элементам множества <tex>S</tex>. |
}} | }} | ||
Версия 21:15, 10 ноября 2013
| Определение: |
Пара называется моноидом, если она удовлетворяет следующим аксиомам:
|
Другими словами, моноид — это полугруппа, в которую добавлен нейтральный элемент. Например, множество натуральных чисел с операцией сложения не является моноидом, а с операцией умножения является.
| Утверждение (О единственности нейтрального элемента): |
Нейтральный элемент в моноиде единственен. |
| Действительно, пусть и — два нейтральных элемента. Тогда имеем: . |
| Определение: |
| Свободным моноидом (англ. free monoid) над множеством обозначается как называется моноид над множеством — набором всевозможных элементов, полученных конечным числом применений ассоциативной операции к элементам множества . |
- тривиальный пример: множество и операция . Тогда , что, очевидно, является моноидом с операцией .
- , операция — сложение. Тогда , так как любое натуральное число является либо нулем, либо суммой конечного числа единиц.
Дадим теперь более формальное определение.
| Определение: |
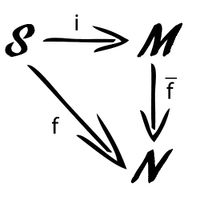
| Свободным моноидом над множеством называется моноид вместе с отображением при условии, что для любого моноида и для любых отображений существует уникальный гомоморфизм моноидов такой, что . |
Это наглядно показано следующей картинкой.