Теорема Фари — различия между версиями
Valery (обсуждение | вклад) |
Valery (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
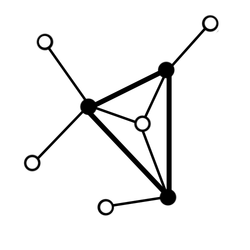
| + | [[File:Fary1.png|thumb|250px|Рисунок 1]] | ||
Теорема была независимо доказана Клаусом Вагнером в 1936 года, Иштваном Фари в 1948ом году и Штейном в 1951ом году. | Теорема была независимо доказана Клаусом Вагнером в 1936 года, Иштваном Фари в 1948ом году и Штейном в 1951ом году. | ||
| Строка 12: | Строка 13: | ||
}} | }} | ||
| − | Разделяющий треугольник представлен на рисунке 1. | + | Разделяющий треугольник представлен на рисунке 1. |
| Строка 21: | Строка 22: | ||
|statement= Любой планарный граф имеет представление на плоскости, в котором все его ребра будут прямыми. | |statement= Любой планарный граф имеет представление на плоскости, в котором все его ребра будут прямыми. | ||
|proof= | |proof= | ||
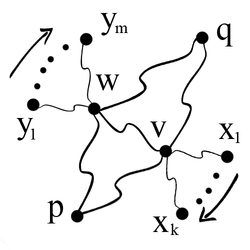
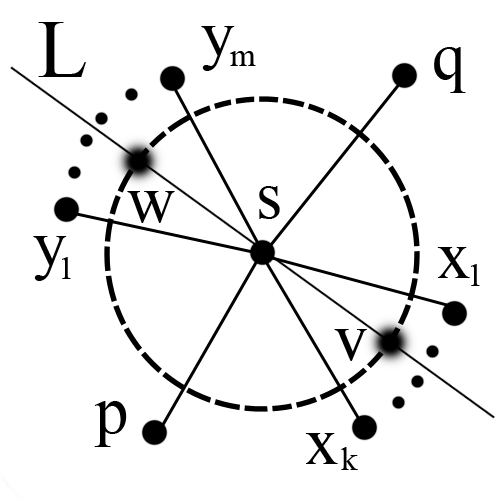
| + | [[File:Fary2.png|thumb|250px|Рисунок 2]] | ||
Докажем теорему для плоской триангуляции графа G. Ее можно достичь, добавив в G необходимое количество ребер. Применим индукцию по числу вершин V(G). Предположим, что графы с числом вершин, меньшим V, мы можем нарисовать требуемым образом. | Докажем теорему для плоской триангуляции графа G. Ее можно достичь, добавив в G необходимое количество ребер. Применим индукцию по числу вершин V(G). Предположим, что графы с числом вершин, меньшим V, мы можем нарисовать требуемым образом. | ||
База: V=3 — тривиально | База: V=3 — тривиально | ||
Переход: V>=4 | Переход: V>=4 | ||
| − | |||
Рассмотрим ребро vw. Если в G нет разделяющих треугольников, то vw – любое. Иначе vw – ребро, инцидентное вершине, находящейся внутри самого глубокого разделяющего треуголька в G. Тогда vw – граница двух граней vwp & vwq. | Рассмотрим ребро vw. Если в G нет разделяющих треугольников, то vw – любое. Иначе vw – ребро, инцидентное вершине, находящейся внутри самого глубокого разделяющего треуголька в G. Тогда vw – граница двух граней vwp & vwq. | ||
Если vw не в разделяющем треугольнике p & q – любые общие соседи v и w. | Если vw не в разделяющем треугольнике p & q – любые общие соседи v и w. | ||
Версия 23:01, 11 ноября 2013
Теорема была независимо доказана Клаусом Вагнером в 1936 года, Иштваном Фари в 1948ом году и Штейном в 1951ом году.
Определения
| Определение: |
| Триангуляция графа — представление графа на плоскости в таком виде, что каждая его грань ограничена тремя ребрами (является треугольником). |
| Определение: |
| Разделяющий треугольник — цикл длины 3 в графе G, внутри и снаружи которого находятся вершины графа. |
Разделяющий треугольник представлен на рисунке 1.
Теорема
| Теорема (Фари): |
Любой планарный граф имеет представление на плоскости, в котором все его ребра будут прямыми. |
| Доказательство: |
|
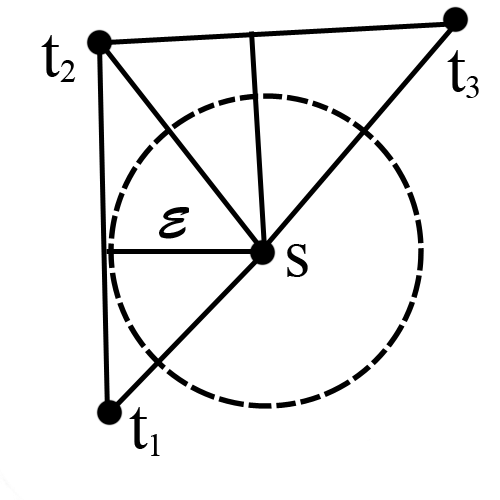
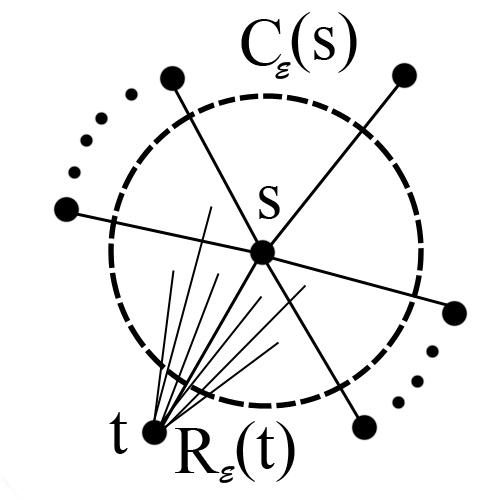
Докажем теорему для плоской триангуляции графа G. Ее можно достичь, добавив в G необходимое количество ребер. Применим индукцию по числу вершин V(G). Предположим, что графы с числом вершин, меньшим V, мы можем нарисовать требуемым образом. База: V=3 — тривиально Переход: V>=4 Рассмотрим ребро vw. Если в G нет разделяющих треугольников, то vw – любое. Иначе vw – ребро, инцидентное вершине, находящейся внутри самого глубокого разделяющего треуголька в G. Тогда vw – граница двух граней vwp & vwq. Если vw не в разделяющем треугольнике p & q – любые общие соседи v и w. Пусть (vp, vw, vq, vx_1, vx_2 … vx_k) & (wq, wv, wp, wy_1, wy_2 … wy_l) – обход по часовой стрелке ребер, исходящих соостветсвенно из v и w. Пусть G' – планарная триангуляция, полученная из G стягиванием ребра vw в вершину s. Заменим пары параллельных ребер vq & wq на sq и vp & wp на sp. Получим вершину s, из которой исходят ребра (sp, sy_1, sy_2 … sy_l, sq, sx_1, sx_2 … sx_k) – по часовой стрелке. Мы получили граф G', с меньшим числом вершин = V - 1 — то есть его можно уложить на плоскости требуемым образом: все ребра прямые (и сохранен обход по часовой стрелке ребер инцидентных s). Для любого E>0 обозначим C_E(s) — круг радиуса E, с вершиной s в центре. Для каждого соседа t вершины s в графе G' обозначим R_E(t) область, содержащую множество всех окрытых отрезков от t до каждой точки из C_E(s). Возьмем E равным минимуму из всех расстояний от вершины s до инцидентных ей вершин и до отрезков, проходящих мимо нее . Тогда получим, что все соседи t вершины s находятся снаружи C_E(s) и только ребра G', пересекающие R_E(t), являются инцидентными s. Проведем линию L через вершину s так, чтобы вершина p лежла с одной ее стороны, а q — с другой (иначе L наложится на ребра sp & sq. ), и L никакое из ребер {sx_i : 1<i<k} и {sy_i : 1<i<l} не лежало на ней. Ребра sq & sq разбивают C_E(s) на две дуги: первая пересекает ребра {sx_i : 1<i<k}, а вторая — ребра {sy_i : 1<i<l}. L пересекает C_E(s) в двух точках. Расположим v & w в этих точках: v на дуге, пересекающей {sx_i : 1<i<k}, а w с другой стороны. Удалим s и инцидентные ей ребра, нарисуем прямые ребра G, инцидентные v и w. Получим, что vw лежит на L. Так как p и q лежат с разных сторон L, ребра, инцидентные v и w, не пересекаются. По выбору E, ребра, инцидентные v и w, не пересекают и другие ребра G. Таким образом желаемая укладка графа G достигнута. Теперь мы можем удалить триангуляцию графа, оставив в графе лишь исходные (уже прямые) ребра. |