Схема алгоритма Диница — различия между версиями
(Добавил уточнение, что слоистую сеть также называют вспомогательной.) |
(→Определение слоистой сети) |
||
| Строка 2: | Строка 2: | ||
Для начала определим для каждой вершины <tex>v</tex> данной сети <tex>G</tex> длину кратчайшего <tex>s \leadsto v</tex> пути из истока и обозначим ее <tex>d[v]</tex> (для этого можно воспользоваться [[Обход в ширину|обходом в ширину]]).<br/> В слоистую сеть включаем только те ребра <tex>(u,v)</tex> исходной сети, для которых <tex>d[u] + 1 = d[v]</tex>. | Для начала определим для каждой вершины <tex>v</tex> данной сети <tex>G</tex> длину кратчайшего <tex>s \leadsto v</tex> пути из истока и обозначим ее <tex>d[v]</tex> (для этого можно воспользоваться [[Обход в ширину|обходом в ширину]]).<br/> В слоистую сеть включаем только те ребра <tex>(u,v)</tex> исходной сети, для которых <tex>d[u] + 1 = d[v]</tex>. | ||
Полученная сеть ациклична, и любой <tex>s \leadsto t</tex> путь в слоистой сети является кратчайшим путём в исходной, из свойств обхода в ширину. | Полученная сеть ациклична, и любой <tex>s \leadsto t</tex> путь в слоистой сети является кратчайшим путём в исходной, из свойств обхода в ширину. | ||
| − | |||
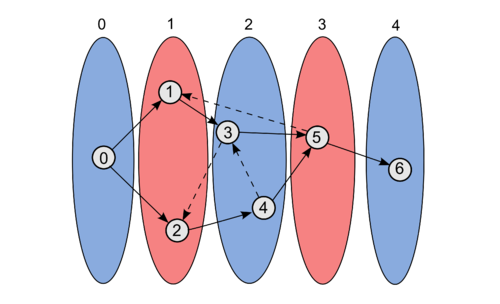
[[Файл:Слоистая_сеть.png|500px |thumb|center| Слоистая сеть с пятью слоями. s = 0, t = 6]] | [[Файл:Слоистая_сеть.png|500px |thumb|center| Слоистая сеть с пятью слоями. s = 0, t = 6]] | ||
<br/>В примере ребра, обозначенные пунктиром, не входят в слоистую сеть. | <br/>В примере ребра, обозначенные пунктиром, не входят в слоистую сеть. | ||
| + | <br/><br/>Слоистую сеть для графа G будем называть '''вспомогательной сетью'''. | ||
== Алгоритм == | == Алгоритм == | ||
Версия 23:03, 26 ноября 2013
Содержание
Определение слоистой сети
Для начала определим для каждой вершины данной сети длину кратчайшего пути из истока и обозначим ее (для этого можно воспользоваться обходом в ширину).
В слоистую сеть включаем только те ребра исходной сети, для которых .
Полученная сеть ациклична, и любой путь в слоистой сети является кратчайшим путём в исходной, из свойств обхода в ширину.
В примере ребра, обозначенные пунктиром, не входят в слоистую сеть.
Слоистую сеть для графа G будем называть вспомогательной сетью.
Алгоритм
Пусть дана сеть. Требуется найти в этой сети поток из в максимальной величины.
Схема алгоритма
- Для каждого ребра данной сети зададим .
- Построим вспомогательную сеть из дополняющей сети данного графа . Если , остановиться и вывести .
- Найдем блокирующий поток в ..
- Дополним поток найденным потоком и перейдем к шагу 2.
Корректность алгоритма
Покажем, что если алгоритм завершается, то на выходе у него получается поток именно максимальной величины.
В самом деле, предположим, что в какой-то момент во вспомогательной сети, построенной для остаточной сети, не удалось найти блокирующий поток. Это означает, что сток вообще не достижим во вспомогательной сети из истока. Но поскольку она содержит в себе все кратчайшие пути из истока в остаточной сети, это в свою очередь означает, что в остаточной сети нет пути из истока в сток. Следовательно, применяя теорему Форда-Фалкерсона, получаем, что текущий поток в самом деле максимален.
Асимптотика алгоритма
| Теорема: |
Расстояние между истоком и стоком строго увеличивается после каждой фазы алгоритма, т.е. , где — значение, полученное на следующей фазе алгоритма. |
| Доказательство: |
| Проведём доказательство от противного. Пусть длина кратчайшего пути из истока в сток останется неизменной после очередной фазы алгоритма. Вспомогательная сеть строится по остаточной. Из предположения следует, что в остаточной сети будет содержаться только рёбра остаточной сети перед выполнением данной фазы, либо обратные к ним. Из этого получаем, что нашёлся путь, который не содержит насыщенных рёбер и имеет ту же длину, что и кратчайший путь. Но этот путь должен был быть «заблокирован» блокирующим потоком, чего не произошло. Получили противоречие. Значит длина изменилась. |
Поскольку длина кратчайшего пути не может превосходить , то, следовательно, алгоритм Диница совершает не более фазы. Таким образом, в зависимости от того, каким алгоритмом нахождения блокирующего потока мы пользовались, весь алгоритм Диница может выполняться за или за . Также возможно достичь асимптотики , если использовать динамические деревья Слетора и Тарьяна.
Реализация
bfs()
.push()
while
.pop
поток из в положителен и не посещена)
.push()
.pop()
makeGl()
bfs()
algorithmDinica()
makeGl()
while ( достижима)
Ищем блокирующий поток
Меняем поток
makeGl()
вывести поток
Источники
- Алгоритм Диница на e-maxx.ru
- Алгоритм Диница на ru.wikipedia.org
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — С. 1296. — ISBN 5-8489-0857-4