Числа Эйлера I и II рода

Числа Эйлера I рода

Числа Эйлера I рода (Eulerian numbers) — количество перестановок чисел от 1 до n таких, что в каждой из них существует ровно m подъемов. Числа Эйлера I рода обозначают как [math]\langle{n\atop m}\rangle [/math] или же [math]A(n, m)[/math].

Определение:

Пусть [math]a[/math] и [math]b[/math] - соседние элементы некоторой перестановки порядка [math]n[/math] причем [math]a \gt b[/math]. Тогда пара [math](a, b)[/math] называется подъемом (ascent) данной перестановки.

Вывод рекуррентной формулы

Пусть у нас есть некая перестановка [math] \pi = \pi_1, \pi_2...\pi_{n-1} [/math]. Тогда операцией вставки элемента с номером n в какую-либо из позиций мы получим [math]n[/math] перестановок вида [math]\theta = \theta_1, \theta_2...\theta_p, n, \theta_q...\theta_{n-1}[/math]. Далее рассмотрим два случая:

1. Количество подъемов в перестановке [math]\theta[/math] равно количеству подъемов в [math]\pi[/math]. Этого можно добиться, вставляя элемент [math]n[/math] на самое первое место в [math]\theta[/math] (всего [math]\langle{n\atop m}\rangle [/math] возможностей) или перед последним последним элементом каждого подъема (еще [math]m \times [/math][math] \langle{n\atop m}\rangle [/math] раз).
2. Количество подъемов в новой перестановке на один больше предыдущего количества. Этого эффекта добиваемся вставкой элемента [math]n[/math] во все места, не подходящие по критерию первого пункта. Таких вставок, как не трудно догадаться, можно совершить [math](n - m)[/math][math]\langle{n\atop m}\rangle[/math].

Тогда рекуррентная формула имеет вид:

[math]\left\langle{n\atop m}\right\rangle = (m + 1)\left\langle{n - 1\atop m}\right\rangle + (n - m)\left\langle{n - 1\atop m - 1}\right\rangle[/math]

Примем также следующее начальное значение:

[math]\left\langle{0\atop m}\right\rangle = [m = 0][/math],

Запись [выражение] означает нотацию Айверсона.

Пример

Рассмотрим все перестановки порядка [math]4[/math], в которых есть ровно 2 подъема (в квадратных скобках один или больше подъемов подряд):

[math] \left\langle{4\atop 2}\right\rangle = 11: [124]3, [13][24], [134]2, [14][23], 2[134], [23][14], [23][41], [24][13], 3[124], [34][12], 4[123], [/math]

Согласно алгоритму вывода рекуррентной формулы мы можем добавить '4' в следующие позиции всех перестановок порядка [math]3[/math] с двумя подъемами, не увеличив количество подъемов:

[math] \left\langle{3\atop 2}\right\rangle = 1: [123] =\gt (4)[123], [1(4)][23], [12(4)]3 [/math]

Далее рассмотрим все перестановки порядка [math]3[/math] с одним подъемом, причем операцией вставки [math]4[/math] мы будем увеличивать количество перестановок на 1:

[math] \left\langle{3\atop 1}\right\rangle = 4:[/math]

[math][13]2 =\gt [13(4)]2, [13][2(4)];[/math]

[math]2[13] =\gt [2(4)][13], 2[13(4)];[/math]

[math][23]1 =\gt [23(4)]1, [23][1(4)];[/math]

[math]3[12] =\gt [3(4)][12], 3[12(4)];[/math]

Таким образом мы убеждаемся в верности формулы:

[math] \left\langle{4\atop 2}\right\rangle = (2 + 1) \left\langle{3\atop 2}\right\rangle + (4 - 2)\left\langle{3\atop 1}\right\rangle = 11;[/math]

Треугольник чисел Эйлера I рода

На значениях [math]n = m[/math] чисел Эйлера I рода можно построить массив [math]n \times m[/math], нижнедиагональная часть которого названа треугольником чисел Эйлера I рода.

	m = 0	1	2	3	4	5	6	7	8	9
n = 0	1	0	0	0	0	0	0	0	0	0
1	1	0	0	0	0	0	0	0	0	0
2	1	1	0	0	0	0	0	0	0	0
3	1	4	1	0	0	0	0	0	0	0
4	1	11	11	1	0	0	0	0	0	0
5	1	26	66	26	1	0	0	0	0	0
6	1	57	302	302	57	1	0	0	0	0
7	1	120	1191	2416	1191	120	1	0	0	0
8	1	247	4293	15619	15619	4293	247	1	0	0
9	1	502	14608	88234	156190	88234	14608	502	1	0

Явная формула

Воспользуемся для вывода треугольником, построенным с помощью рекурсивного варианта формулы.

Следует заметить, что первый элемент каждой [math]m[/math]-той строки равен 1, а второй --- [math]2^{m} - (m + 1)[/math]. Третий выражается как

[math]3^{m}-(m + 1)2^m + \frac{(m+1)m}{2};[/math]

и так далее. Первые три элемента могут быть записаны в форме:

[math]\left\langle{m\atop 1}\right\rangle = {{m + 1} \choose {0}}1^{m}[/math]

[math]\left\langle{m\atop 2}\right\rangle = {{m + 1} \choose {0}}2^{m} + {{m + 1} \choose {1}}1^{m}[/math]

[math]\left\langle{m\atop 3}\right\rangle = {{m + 1} \choose {0}}3^{m} - {{m + 1} \choose {1}}2^{m} + {{m + 1} \choose {2}}1^{m}[/math]

Тогда нетрудно проверить, что эта сумма продолжается именно таким образом и, следовательно, мы можем обобщить ее в "строгом виде" как:

[math]\left\langle{m\atop n}\right\rangle = \sum\limits_{j=1}^{n+1} (-1)^{n-j+1} {m+1\choose n-j+1}j^{m}[/math]

Существует также иная широко используемая явная формула:

[math]\left\langle{n\atop m}\right\rangle = \sum\limits_{k=0}^{m} {n+1\choose k} (m+1-k)^n(-1)^k[/math]

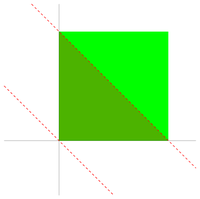
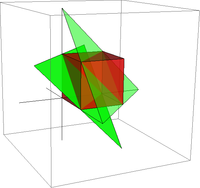
Связь чисел Эйлера I рода с сечениями гиперкубов

Теорема:

Число [math]\frac{1}{n!}\left\langle{n\atop m}\right\rangle[/math] выражает объем части [math]n[/math]-мерного единичного гиперкуба, ограниченного гиперплоскостями [math]x_1+x_2+\dots+x_n=m[/math] и [math]x_1+x_2+\dots+x_n=m-1[/math];

Доказательство:

[math]\triangleright[/math]

Для доказательства этого факта нам потребуется следующая теорема: Теорема (Об объемах сечений [math]n[/math]-мерных гиперкубов полупространствами): Пусть [math]w \in \mathbb{R}[/math] - вектор с ненулевыми компонентами ([math]w = {w_1, w_2 ... w_n}[/math]), а [math]z \in \mathbb{R}_+[/math]. Тогда верно следующее равенство: [math]\mathrm{Vol}_{n}(G^n_{w,z} \cap I^{n}) = \frac{1}{n! \prod\limits_{i=1}^{n}w_i} \sum\limits_{K \subseteq [n]} (-1)^{|K|}(z-w \cdot 1_K)^n_+[/math] [math]G_{w, z}^{n} := \{x \in \mathbb{R}^{n} : (w \cdot x) \le z \}[/math] - полупространство; [math]I^n := [0,1]^n[/math]; [math][n] := \{1,2...n\}[/math]; [math]1_K[/math], где [math]K[/math] - множество, изоморфное подмножеству [math]\mathbb{N}[/math], — вектор, где значения координат с номерами, входящими в [math]K[/math], равны 1, а остальные — нули; Для [math]r \in \mathbb{R}[/math] и [math]n \in \mathbb{N}[/math] : [math]r^n_+ := (\max{\{r, 0\}})^n[/math]. Доказательство: [math]\triangleright[/math] С доказательством можно ознакомиться по этой ссылке. [math]\triangleleft[/math] m = 2, n = 1. V = 1/2 m = 3, n = 2. V = 1/6 Рассмотрим пересечение гиперкуба полупространством [math]G^n_{1_{[n]},m}[/math]. Вектор [math]1_{[n]}[/math] появляется здесь ввиду того, как мы определили в формулировке секущие гиперплоскости ([math]x_1+x_2+...+x_n = m | m+1[/math]). Очевидно, что при данном значении вектора произведение [math]\prod\limits_{i=1}^{n}w_i[/math] равно единице. Рассмотрим выражение, стоящее под знаком суммы. При итерации по подмножествам [math][n][/math] равной мощности будут получаться одинаковые слагаемые, так как выражение [math](-1)^{|K|}(z-w \cdot 1_K)^n_+[/math] зависит лишь от мощности итерируемого в сумме подмножества [math]K[/math] — скалярное произведение [math]w \cdot 1_K[/math] одинаково за счет того лишь факта, что оно вычисляется как сумма произведений соответствующих координат, где ровно [math]n - |K|[/math] их обращаются в ноль. Такое скалярное произведение будет равно мощности [math]K[/math]. Заменим итератор суммы значением мощности множества [math]K[/math]. Также ограничим верхний индекс суммирования значением [math]m+1[/math], так как при больших значениях [math]j[/math] слагаемое будет обращаться в ноль ([math]r^n_+[/math]). Отсюда имеем [math]{n \choose j}[/math] таких одинаковых слагаемых, где [math]j = |K|[/math]. Тогда перейдем от первоначальной формулировки теоремы к следующей: [math]\mathrm{Vol}_{n}(G^n_{1_{[n]},m} \cap I^{n}) = \frac{1}{n!}\sum\limits_{j = 0}^{m + 1} (-1)^{j}{n \choose j}(m-j)^n[/math] Положим [math]W_n^m[/math] - фигура, образованная сечением гиперкуба [math][0,1]^{n}[/math] плоскостями [math]\sum\limits_{i=1}^{n} x_{i} = m[/math] и [math]\sum\limits_{i=1}^{n} x_{i} = m+1[/math]. [math]W_n^m := \{ x \in \mathbb{R} : m \le x \cdot 1_{[n]} \le m+1 \} \cap I^{n}[/math] Тогда перейдем к следующему равенству: [math]\mathrm{Vol}_{n}(W_n^m) = \mathrm{Vol}_n(G_{1_{[n]},m+1}^{n} \cap I^n) - \mathrm{Vol}_n(G_{1_{[n]},m}^{n} \cap I^n)[/math] [math]= \frac{1}{n!}[\sum\limits_{j=0}^{m+1}(-1)^{j}{n \choose j}(m+1-j)^{n} - \sum\limits_{j=0}^{m}(-1)^{j}{n \choose j}(m-j)^{n}][/math] [math] = \frac{1}{n!}\sum\limits_{j=0}^{m+1}(-1)^j{n+1 \choose j}(m+1-j)^n[/math] [math] = \frac{1}{n!}\left\langle{n\atop m}\right\rangle[/math]

[math]\triangleleft[/math]

Свойства

1. Нетрудно увидеть, что каждый ряд ненулевых значений симметричен относительно своей середины, то есть:

   [math]\left\langle{n\atop m}\right\rangle = \left\langle{n\atop (n-1) - k}\right\rangle,\ n \ge 1,\ 0 \le k \le n-1. \, [/math]

2. Сумма всех значений каждого ряда равна [math] n! [/math]:

   [math]\sum\limits_{k=0}^{n} \left\langle{n\atop m}\right\rangle = n!,\ n \ge 0, \,[/math]

3. Связь чисел Эйлера I рода с числом сочетаний:

   [math]\sum\limits_{m=0}^n (-1)^m {\left\langle{n\atop m}\right\rangle}{n-1\choose m}^{-1}=0.[/math]

4. Вероятность того, что сумма [math]n[/math] независимых равномерно распределённых в отрезке [math][0,1][/math] переменных лежит между [math]m-1[/math] и [math]m[/math] равна [math]\frac{1}{n!}\left\langle{n\atop m}\right\rangle[/math].

Числа Эйлера II рода

Числа Эйлера II рода (Eulerian numbers of the second kind) — количество перестановок мультимножества от [math]1[/math] до [math]n[/math] вида [math]\{1,1,2,2..n,n\}[/math], обладающих свойством "все элементы перестановки, встречающиеся между двумя вхождниями [math]z[/math] для любого [math]z[/math], больше, чем [math]z[/math]", таких, что в каждой из них существует ровно [math]m[/math] подъемов. Числа Эйлера II рода обозначаются как [math] \scriptstyle \left\langle \!\! \left\langle {n \atop m} \right\rangle \!\! \right\rangle [/math]

Пример

Рассмотрим [math] n = 3[/math]. Тогда существует 15 перестановок такого вида, среди которых одна не имеет подъемов, 8 штук имеют всего 1 подъем, и 6 перестановок имеют 2 подъема:

[math] 332211,\; [/math]

[math] 221[13]3,\; 22[13]31,\; 2[23]311,\; [23]3211,\; 1[13]322,\; [13]3221,\; 331[12]2,\; 33[12]21, [/math]

[math]1[12][23]3,\; [12]2[13]3,\; 1[123]32,\; [123]321,\; [13]3[12]2,\; [12][23]31. [/math]

Лемма:

Количество перестановок мультимножества [math]\{1,1,2,2..n,n\}[/math] со свойством "все элементы перестановки, встречающиеся между двумя вхождниями [math]z[/math] для любого [math]z[/math], больше, чем [math]z[/math]" равно двойному факториалу [math](2n-1)!![/math].

Рекуррентная формула

Числа Эйлера II рода можно выразить рекурсивно следующим образом:

[math] \left\langle \!\! \left\langle {n \atop m} \right\rangle \!\! \right\rangle = (2n-m-1) \left\langle \!\! \left\langle {n-1 \atop m-1} \right\rangle \!\! \right\rangle + (m+1) \left\langle \!\! \left\langle {n-1 \atop m} \right\rangle \!\! \right\rangle, [/math]

С начальным условием для [math]n = 0[/math]:

[math] \left\langle \!\! \left\langle {0 \atop m} \right\rangle \!\! \right\rangle = [m=0]. [/math]

Треугольник чисел Эйлера II рода

Значения чисел Эйлера II рода для [math]0 \le n \le m \le 9[/math] представлены в данном массиве. Нижнедиагональная его часть называется треугольником чисел Эйлера II рода.

	m = 0	1	2	3	4	5	6	7	8	9
n = 0	1	0	0	0	0	0	0	0	0	0
1	1	0	0	0	0	0	0	0	0	0
2	1	2	0	0	0	0	0	0	0	0
3	1	8	6	0	0	0	0	0	0	0
4	1	22	58	24	0	0	0	0	0	0
5	1	52	328	444	120	0	0	0	0	0
6	1	114	1452	4400	3708	720	0	0	0	0
7	1	240	5610	32120	58140	33984	5040	0	0	0
8	1	494	19950	195800	644020	785304	341136	40320	0	0
9	1	1004	67260	1062500	5765500	12440064	11026296	3733920	362880	0

Ссылки

• Eulerian number — Wikipedia
• Треугольник чисел Эйлера I рода — OEIS Wiki
• Eulerian number — Math Pages
• Числа Эйлера — Wolfram Mathworld
• A Refinement of the Eulerian numbers
• Доказательство свойства о взаимосвязи чисел Эйлера I рода и объема сечений гиперкуба