Диаметр множества точек (вращающиеся калиперы) — различия между версиями
Megabyte (обсуждение | вклад) |
Megabyte (обсуждение | вклад) |
||
| Строка 25: | Строка 25: | ||
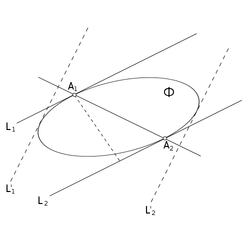
Так как <tex>A_1</tex> и <tex>A_2</tex> {{---}} какие угодно граничные точки фигуры <tex>\Phi</tex>, принадлежащие соответственно прямым <tex>L_1</tex> и <tex>L_2</tex>, то из перпендикулярности отрезка <tex>A_1A_2</tex> к прямым <tex>L_1</tex> и <tex>L_2</tex> следует, что ни одна из прямых <tex>L_1</tex>, <tex>L_2</tex> не может иметь с фигурой <tex>\Phi</tex> целый общий отрезок. Другими словами, каждая из этих прямых содержит единственную граничную точку фигуры <tex>\Phi</tex>. | Так как <tex>A_1</tex> и <tex>A_2</tex> {{---}} какие угодно граничные точки фигуры <tex>\Phi</tex>, принадлежащие соответственно прямым <tex>L_1</tex> и <tex>L_2</tex>, то из перпендикулярности отрезка <tex>A_1A_2</tex> к прямым <tex>L_1</tex> и <tex>L_2</tex> следует, что ни одна из прямых <tex>L_1</tex>, <tex>L_2</tex> не может иметь с фигурой <tex>\Phi</tex> целый общий отрезок. Другими словами, каждая из этих прямых содержит единственную граничную точку фигуры <tex>\Phi</tex>. | ||
| − | {{Лемма | + | {| border="0" width="100%" |
| + | |{{Лемма | ||
|statement= | |statement= | ||
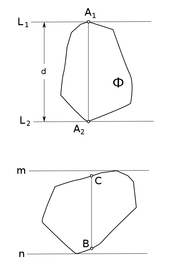
| − | Диаметр выпуклого | + | Диаметр выпуклого многоугольника равен максимальному расстоянию между параллельными опорными прямыми. |
|proof= | |proof= | ||
| − | + | Пусть <tex>\Phi</tex> {{---}} выпуклая фигура, <tex>L_1</tex> и <tex>L_2</tex> {{---}} параллельные опорные прямые, расстояние между которыми имеет наибольшее возможное значение <tex>d</tex>, <tex>A_1</tex> и <tex>A_2</tex> {{---}} общие точки фигуры <tex>\Phi</tex> и прямых <tex>L_1</tex> и <tex>L_2</tex> соответственно. По предыдущей лемме <tex>A_1A_2</tex> перпендикулярен к прямым <tex>L_1</tex>, <tex>L_2</tex>, следовательно, его длина равна <tex>d</tex>. Докажем, что расстояние между любыми двумя точками фигуры <tex>\Phi</tex> не преводходит <tex>d</tex>. Действительно, если <tex>B</tex> и <tex>C</tex> {{---}} какие-либо две точки фигуры <tex>\Phi</tex>, а <tex>m</tex> и <tex>n</tex> {{---}} опорные прямые, перпендикулярные к отрезку <tex>BC</tex>, то отрезок <tex>BC</tex> не превосходит расстояния между прямыми <tex>m</tex> и <tex>n</tex>, которое в свою очередь не превосходит <tex>d</tex>. Следовательно, длина <tex>BC</tex> не может быть больше <tex>d</tex>. | |
}} | }} | ||
| − | + | |[[Файл:max_parallel.png|170px|thumb|right]] | |
| + | |} | ||
== Литература == | == Литература == | ||
* ''M.I. Shamos'' Computational geometry, 1978 {{---}} С. 76. | * ''M.I. Shamos'' Computational geometry, 1978 {{---}} С. 76. | ||
Версия 15:51, 8 января 2014
Есть множество точек на плоскости. Нужно найти две самые удалённые из них.
Найдём выпуклую оболочку исходного множества и получим более простую задачу: найти две наиболее удалённые вершины в выпуклом многоугольнике. Сделать это можно за линейное время с помощью метода, который называется вращающиеся калиперы (англ. rotating calipers).
Постановка задачи
Пусть — выпуклый многоугольник, в котором порядок обхода вершин направлен против часовой стрелки, и никакие три последовательные точки не лежат на одной прямой. Найти пару чисел , такие, что максимально.
Вращающиеся калиперы
| Определение: |
| Прямая называется опорной прямой (англ. line of support) для многоугольника , если его внутренность лежит по одну сторону от , при этом проходит хотя бы через одну из вершин . |
|
Так как и — какие угодно граничные точки фигуры , принадлежащие соответственно прямым и , то из перпендикулярности отрезка к прямым и следует, что ни одна из прямых , не может иметь с фигурой целый общий отрезок. Другими словами, каждая из этих прямых содержит единственную граничную точку фигуры .
|
Литература
- M.I. Shamos Computational geometry, 1978 — С. 76.
- Яглом И.М., Болтянский В.Г. Выпуклые фигуры, 1951 — С. 20, 144.