Выпуклая оболочка в n-мерном пространстве — различия между версиями
| Строка 1: | Строка 1: | ||
| − | {{ | + | {{ptready}} |
| − | Рассмотрим трёхмерный случай. <tex>n</tex>-мерный | + | Рассмотрим трёхмерный случай. <tex>n</tex>-мерный сводится к трёхмерному. |
| − | == | + | ==Суть алгоритма== |
Выберем любые две точки <tex>p_1</tex> и <tex>p_2</tex>. Далее из оставшихся выберем точку <tex>p_3</tex>, которая не лежит на прямой, образованной точками <tex>p_1</tex> и <tex>p_2</tex>. После этого выберем точку <tex>p_4</tex>, которая не лежит на плоскости, образованной точками <tex>p_1, p_2</tex> и <tex>p_3</tex>. Если этого сделать не получилось, то запустим алгоритм для поиска выпуклой оболочки на плоскости. | Выберем любые две точки <tex>p_1</tex> и <tex>p_2</tex>. Далее из оставшихся выберем точку <tex>p_3</tex>, которая не лежит на прямой, образованной точками <tex>p_1</tex> и <tex>p_2</tex>. После этого выберем точку <tex>p_4</tex>, которая не лежит на плоскости, образованной точками <tex>p_1, p_2</tex> и <tex>p_3</tex>. Если этого сделать не получилось, то запустим алгоритм для поиска выпуклой оболочки на плоскости. | ||
| − | Так мы получили тетраэдр <tex>p_1 p_2 p_3 p_4</tex>. Сделаем random shuffle оставшихся точек <tex>p_5, ..., p_n</tex>. | + | Так мы получили тетраэдр <tex>p_1 p_2 p_3 p_4</tex>, который является выпуклой оболочкой этих четырёх точек. Сделаем random shuffle оставшихся точек <tex>p_5, ..., p_n</tex> и будем добавлять их по одной в выпуклую оболочку. Если <tex>p_i</tex> внутри или на границах выпуклой оболочки, то выпуклая оболочка не меняется на этом шаге. Иначе из имеющейся выпуклой оболочки надо удалить все видимые из данной точки грани и добавить новые — из точки до каждого ребра, образующего horizon (см. картинки). После этого нужно смержить соседние грани, которые получились копланарными. |
| + | |||
| + | [[Файл:3dconvexhullhorizon.png]] [[Файл:3dconvexhulladd.png]] | ||
Версия 11:25, 17 января 2014
| Конспект написан не до конца, но основные вещи уже есть. |
Рассмотрим трёхмерный случай. -мерный сводится к трёхмерному.
Суть алгоритма
Выберем любые две точки и . Далее из оставшихся выберем точку , которая не лежит на прямой, образованной точками и . После этого выберем точку , которая не лежит на плоскости, образованной точками и . Если этого сделать не получилось, то запустим алгоритм для поиска выпуклой оболочки на плоскости.
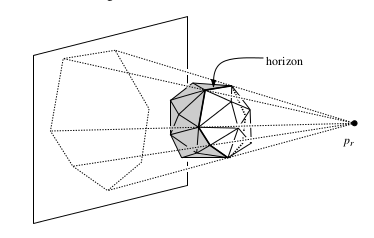
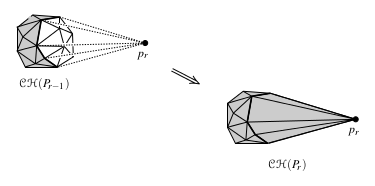
Так мы получили тетраэдр , который является выпуклой оболочкой этих четырёх точек. Сделаем random shuffle оставшихся точек и будем добавлять их по одной в выпуклую оболочку. Если внутри или на границах выпуклой оболочки, то выпуклая оболочка не меняется на этом шаге. Иначе из имеющейся выпуклой оболочки надо удалить все видимые из данной точки грани и добавить новые — из точки до каждого ребра, образующего horizon (см. картинки). После этого нужно смержить соседние грани, которые получились копланарными.