Пересечение полуплоскостей, связь с выпуклыми оболочками — различия между версиями
Igorjan94 (обсуждение | вклад) м |
Igorjan94 (обсуждение | вклад) м |
||
| Строка 11: | Строка 11: | ||
<tex> D(Y = kX + b) = P(k, -b) </tex> | <tex> D(Y = kX + b) = P(k, -b) </tex> | ||
| + | |||
| + | Это отображение не рассматривает вертикальные прямые, поэтому их мы рассмотрим в конце отдельно. | ||
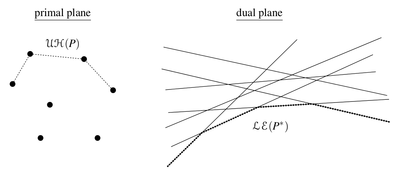
[[Файл:dual.png|400px|thumb|right|Совпадение верхнего CH и нижней огибающей]] | [[Файл:dual.png|400px|thumb|right|Совпадение верхнего CH и нижней огибающей]] | ||
Версия 23:59, 21 февраля 2014
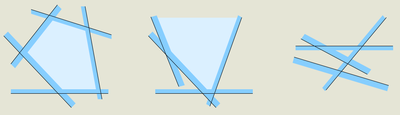
Задача: есть конечное множество полуплоскотей, найти фигуру их пересечения или сообщить что оно пусто.
Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство — Пересечение выпуклых фигур выпукло, а полуплоскоть выпукла)
Рассмотрим отображение между точками и прямыми, такое что:
Это отображение не рассматривает вертикальные прямые, поэтому их мы рассмотрим в конце отдельно.
Будем обозначать, что ,
Факт дуализма:
- Точка лежит под/на/над прямой тогда и только тогда, когда лежит под/на/над прямой ;
Тогда точка принадлежит тогда и только тогда, когда существует такая не вертикальная прямая , что лежит под .
Перефразируем для dual-пространства:
- Существует точка на прямой лежит под любой прямой из .
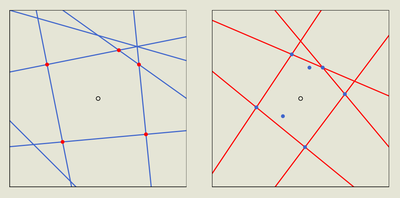
Рассмортим верхний конвекс-халл точек (англ. upper convex hull) и нижнюю огибающей прямых (англ. lower envelope). Точки в появляются в по увелечению х-координаты. Прямые в появляются в по уменьшению угла наклона. Так как угол наклона соответствует х-координате, то список точек слева-направо соответствует списку справа-налево ребер . Таким образом верхний конвекс-халл соответствует нижней огибающей прямых. Аналогично для нижнего СН и верхней огибающей.
Более формально: точки — ребро верхнего конвекс-халла тогда и только тогда, когда все остальные точки из лежат ниже прямой, проходящей через это ребро. В dual-пространстве получаем, что лежат над точкой пересечения и . Это как раз условие, что — вершина .
Таким образом получаем алгоритм:
- Считаем . (полуплоскости, смотрящие вверх)
- Считаем . (полуплоскости, смотрящие вниз)
- Считаем . (вертикальные полуплоскости, смотрящие направо)
- Считаем . (вертикальные полуплоскости, смотрящие налево)
- Пускаем заметающую вертикальную прямую и получаем пересечение
Стоит уточнить, что каждое из этих множеств может быть пусто. Тогда мы не рассматриваем с ним объединение. Однако в результате мы можем получить пустое множество. Это главное отличние пересечения полуплоскостей и конвекс-халла.
Источники
- Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars (2008), Computational Geometry: Algorithms and Applications (3rd edition), Springer-Verlag, ISBN 978-3-540-77973-5 Chapter 11 page 253-254
- http://wwwisg.cs.uni-magdeburg.de/ag/lehre/SS2012/GAG/slides/V12.pdf