|
|
| Строка 1: |
Строка 1: |
| | [[Файл:samplesHalfspaces.png|400px|thumb|right|Пересечение существует и выпукло, неограничено или пусто]] | | [[Файл:samplesHalfspaces.png|400px|thumb|right|Пересечение существует и выпукло, неограничено или пусто]] |
| − | [[Файл:halfSpaces.png|400px|thumb|right|Нужна ли нам верхняя полуплоскость?]] | + | [[Файл:halfSpaces.png|400px|thumb|right|Нужна ли нам полуплоскость <tex> l'' </tex>?]] |
| | | | |
| | Задача: есть конечное множество полуплоскотей, найти фигуру их пересечения или сообщить что оно пусто. | | Задача: есть конечное множество полуплоскотей, найти фигуру их пересечения или сообщить что оно пусто. |
| Строка 61: |
Строка 61: |
| | | | |
| | От пересечения цепочек напрямую зависит фигура пересечения: неограниченная область получается если одна из цепочек пуста, а ограниченная {{---}} когда обе цепочки не пусты и пересекаются. | | От пересечения цепочек напрямую зависит фигура пересечения: неограниченная область получается если одна из цепочек пуста, а ограниченная {{---}} когда обе цепочки не пусты и пересекаются. |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | Рассмотрим отображение <tex> D </tex> между точками и прямыми, такое что:
| |
| − |
| |
| − | <tex> D(P(k, b)) = (Y = kX - b) </tex>
| |
| − |
| |
| − | <tex> D(Y = kX + b) = P(k, -b) </tex>
| |
| − |
| |
| − | Это отображение не рассматривает вертикальные прямые, поэтому их мы рассмотрим в конце отдельно.
| |
| − |
| |
| − | [[Файл:dual.png|400px|thumb|right|Совпадение верхнего CH и нижней огибающей]]
| |
| − | Будем обозначать, что <tex> D(p) = p^* </tex>, <tex> D(l) = l^* </tex>
| |
| − |
| |
| − | Факт дуализма:
| |
| − | * Точка <tex> p </tex> лежит под/на/над прямой <tex> l </tex> тогда и только тогда, когда <tex> D(l) </tex> лежит под/на/над прямой <tex> D(p) </tex>;
| |
| − | Тогда точка <tex> p \in P = \cup p_i </tex> принадлежит <tex> UH(P) </tex> тогда и только тогда, когда существует такая не вертикальная прямая <tex> l </tex>, что <tex> \forall i : p_i </tex> лежит под <tex> l </tex>.
| |
| − |
| |
| − | Перефразируем для dual-пространства:
| |
| − | * Существует точка <tex> l^* </tex> на прямой <tex> p^* \in P^* : l^* </tex> лежит под любой прямой из <tex> P^*</tex>.
| |
| − |
| |
| − | Рассмортим верхний конвекс-халл точек <tex> P </tex> (англ. ''upper convex hull'') и нижнюю огибающей прямых <tex> P^* </tex> (англ. ''lower envelope''). Точки в <tex> P </tex> появляются в <tex> UH(P) </tex> по увелечению х-координаты. Прямые в <tex> P^* </tex> появляются в <tex> LE(P^*) </tex> по уменьшению угла наклона. Так как угол наклона соответствует х-координате, то список точек <tex> UH(P) </tex> слева-направо соответствует списку справа-налево ребер <tex> LE(P^*) </tex>. Таким образом верхний конвекс-халл соответствует нижней огибающей прямых. Аналогично для нижнего СН и верхней огибающей.
| |
| − |
| |
| − | Более формально: точки <tex> p, q \in P : pq </tex> {{---}} ребро верхнего конвекс-халла тогда и только тогда, когда все остальные точки из <tex> P </tex> лежат ниже прямой, проходящей через это ребро. В dual-пространстве получаем, что <tex> \forall r^*, r \in P \setminus \{p, q\} </tex> лежат над точкой пересечения <tex> p^* </tex> и <tex> q^* </tex>. Это как раз условие, что <tex> p^* \cap q^* </tex> {{---}} вершина <tex> LE(P^*) </tex>.
| |
| − |
| |
| − | Таким образом получаем алгоритм:
| |
| − | * Считаем <tex> H_+ </tex>. (полуплоскости, смотрящие вверх)
| |
| − | * Считаем <tex> H_- </tex>. (полуплоскости, смотрящие вниз)
| |
| − | * Считаем <tex> H_> </tex>. (вертикальные полуплоскости, смотрящие направо)
| |
| − | * Считаем <tex> H_< </tex>. (вертикальные полуплоскости, смотрящие налево)
| |
| − | * Пускаем заметающую вертикальную прямую и получаем пересечение <tex> H_+ \cap H_- \cap H_> \cap H_< </tex>
| |
| − | Стоит уточнить, что каждое из этих множеств может быть пусто. Тогда мы не рассматриваем с ним объединение. Однако в результате мы можем получить пустое множество. Это главное отличние пересечения полуплоскостей и конвекс-халла.
| |
| | | | |
| | == Источники == | | == Источники == |
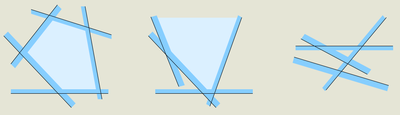
Пересечение существует и выпукло, неограничено или пусто
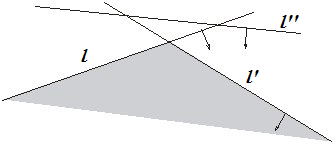
Нужна ли нам полуплоскость
[math] l'' [/math]?
Задача: есть конечное множество полуплоскотей, найти фигуру их пересечения или сообщить что оно пусто.
Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство — Пересечение выпуклых фигур выпукло, а полуплоскоть выпукла)
Пусть у нас прямые заданы уравнениями вида [math] Ax + By + C = 0 [/math]. Тогда предикат(см. рисунок) проверки того, что прямая [math] l'' : A''x + B''y + C'' = 0 [/math] лежит над пересечением прямых [math] l : Ax + By + C = 0 [/math] и [math] l' : A'x + B'y + C' = 0 [/math] будет равен [math]
\begin{vmatrix}
A & B & C \\
A' & B' & C' \\
A'' & B'' & C''
\end{vmatrix}
[/math].
Докажем это. Для проверки предиката нам надо определить знак выражения [math] A''x_0 + B''y_0 + C'' [/math], где [math] (x_0, y_0) [/math] — точка пересечения прямых [math] l' [/math] и [math] l [/math]. Эту точку можно найти из уравнения [math] \begin{pmatrix}
A & B\\
A' & B'
\end{pmatrix}
\begin{pmatrix}
x_0\\
y_0
\end{pmatrix} =
\begin{pmatrix}
-C\\
-C'
\end{pmatrix}
[/math]. Решением будет [math]
\begin{pmatrix}
x_0\\
y_0
\end{pmatrix} =
\frac{
\begin{pmatrix}
B' & -B\\
-A' & A
\end{pmatrix}
\begin{pmatrix}
-C\\
-C'
\end{pmatrix}}
{
\begin{vmatrix}
A & B\\
A' & B'
\end{vmatrix}
}
[/math]. Подставим его в [math] A''x_0 + B''y_0 + C'' [/math] и домножим на определитель.
[math] A'' (B'; -B)(-C; -C') + B'' (-A'; A)(-C; -C') + C \begin{vmatrix} A & B \\ A' & B' \end{vmatrix} = A'' \begin{vmatrix} B' & B \\ -C' & -C \end{vmatrix} - B'' \begin{vmatrix} A' & A \\ -C' & -C \end{vmatrix} + C'' \begin{vmatrix} A & A' \\ B & B' \end{vmatrix} = \begin{vmatrix} A'' & A' & A \\ B'' & B' & B \\ -C'' & -C' & -C \end{vmatrix} = \begin{vmatrix} A & B & C \\
A' & B' & C' \\
A'' & B'' & C'' \end{vmatrix} [/math]
Таким образом если представить прямую [math] Ax + By + C = 0 [/math] как точку с координатами [math] (A, B, C) [/math], где [math] C [/math] — однородная координата, то этот предикат — всего лишь поворот, а проверка предиката — проверка очередной точки в обходе Грэхема для нахождения выпуклой оболочки.
Алгоритм:
- Отсортировать все полуплоскости по углу наклона;
- Запустить обход Грэхема для полуплоскостей, смотрящих вниз (с предикатом-определителем);
- То же самое для смотрящих вверх;
- Пересечь две цепочки.
От пересечения цепочек напрямую зависит фигура пересечения: неограниченная область получается если одна из цепочек пуста, а ограниченная — когда обе цепочки не пусты и пересекаются.
Источники

