Пересечение отрезков на сфере — различия между версиями
Korektur (обсуждение | вклад) |
|||
| Строка 33: | Строка 33: | ||
|statement=Если два отрезка на сфере пересекаются, то все их четыре точки находятся в одной полусфере. | |statement=Если два отрезка на сфере пересекаются, то все их четыре точки находятся в одной полусфере. | ||
|proof= | |proof= | ||
| + | [[Файл:Sphere3.jpg|right|1000|thumb|Плоскость ОАХ]] | ||
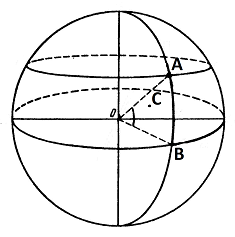
Пусть отрезки: <tex>AB</tex> и <tex>CD</tex>. Точка пересечения <tex>X</tex>. Центр сферы - начало координат <tex>O</tex>. | Пусть отрезки: <tex>AB</tex> и <tex>CD</tex>. Точка пересечения <tex>X</tex>. Центр сферы - начало координат <tex>O</tex>. | ||
Найдем нужную полусферу. Это будет полусфера от окружности точек <tex>A</tex> и <tex>C</tex>, ориентированная так, чтобы содержать <tex>X</tex>.Проведем плоскость <tex>OAX</tex>, пересечем ее со сферой. На полученной окружности возьмем точку <tex>A'</tex> - диаметрально противоположную точке <tex>A</tex>. Точка <tex>B</tex> находится в нашей полусфере, потому что она находится "ближе" точки <tex>A'</tex>. Если бы она была дальше точки <tex>A'</tex>, то мы бы провели отрезок <tex>AB</tex> через другую половину сферы, и соответственно, точка <tex>X</tex> была бы не в выбранной полусфери. | Найдем нужную полусферу. Это будет полусфера от окружности точек <tex>A</tex> и <tex>C</tex>, ориентированная так, чтобы содержать <tex>X</tex>.Проведем плоскость <tex>OAX</tex>, пересечем ее со сферой. На полученной окружности возьмем точку <tex>A'</tex> - диаметрально противоположную точке <tex>A</tex>. Точка <tex>B</tex> находится в нашей полусфере, потому что она находится "ближе" точки <tex>A'</tex>. Если бы она была дальше точки <tex>A'</tex>, то мы бы провели отрезок <tex>AB</tex> через другую половину сферы, и соответственно, точка <tex>X</tex> была бы не в выбранной полусфери. | ||
Версия 09:44, 23 апреля 2014
Постановка задачи
Дано два отрезка на сфере. Необходимо узнать пересекаются ли они.
Проверка на пересечение
Сопоставим каждой точке на сфере луч, исходящий из центра сфера и проходящий через эту точку. Тогда лучи сопоставляемые двум точкам будут образовывать плоскость. Необходимо научиться проверять лежит данная точка в плоскости образованной двумя другими точками. Итак у нас есть точки и образующие плоскость, также есть точка . Необходимо узнать расположение этой точки относительно плоскости. Вспомним о повороте. Необходимо посчитать определитель матрицы поворота и сравнить его знак с нулем.
Рассмотрим три случая:
- тогда точка лежит над плоскостью, образованной точками и .
- тогда точка лежит под плоскостью, образованной точками и .
- тогда точка лежит на плоскости, образованной точками и .
| Лемма (1): |
Если два отрезка на сфере пересекаются, то все их четыре точки находятся в одной полусфере. |
| Доказательство: |
|
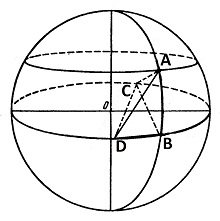
Пусть отрезки: и . Точка пересечения . Центр сферы - начало координат . Найдем нужную полусферу. Это будет полусфера от окружности точек и , ориентированная так, чтобы содержать .Проведем плоскость , пересечем ее со сферой. На полученной окружности возьмем точку - диаметрально противоположную точке . Точка находится в нашей полусфере, потому что она находится "ближе" точки . Если бы она была дальше точки , то мы бы провели отрезок через другую половину сферы, и соответственно, точка была бы не в выбранной полусфери. Далее повторим рассуждения для точек и . |
Соединив концы отрезков, получим тетрэдр.
| Утверждение: |
Если центр шара принадлежит тетраэдру, образованному концами отрезков, то отрезки лежат в разных полушариях. |
Для того чтобы определить принадлежит ли центр шара тетраэдру, необходимо найти грань тетраэдра, которая будет отсекать тетрэдр от центра шара, если такой грани не существует, то центра шара принадлежит тетраэдру, следовательно отрезки находятся в разных полушариях, следовательно они не пересекаются. Для того, чтобы найти такую грань, необходимо для каждой пары точек проверить поворот противоположной точки и центра окружности, и если знаки определителей матриц поворота оказались разные, то такая грань найдена.
Рассмотрим отрезки и . Проверим их на пересечение. Для этого возьмем отрезок и посчитаем для него следующее соотношение
где вместо необходимо поочередно подставить и . И если хотя бы для одной точки , то отрезки пересекаются и точка пересечения лежит на .