Префикс-функция

Префикс-функция строки [math]s[/math] — функция [math]\pi(i) = \max\limits_{k = 1..i - 1} \{ 0, k : [/math] [math]s[1..k] = s[i - k + 1..i] \}[/math].

Алгоритм

Наивный алгоритм вычисляет префикс функцию непосредственно по определению, сравнивая префиксы и суффиксы строк.

Псевдокод

Prefix_function ([math]s[/math])
     [math]\pi[/math] = [0,..,0]
     for i = 1 to n
         for k = 1 to i - 1
             if s[1..k] == s[i - k + 1..i]
                 [math]\pi[/math][i] = k
     return [math]\pi[/math]

Пример

Рассмотрим строку abcabcd, для которой значение префикс-функции равно [math][0,0,0,1,2,3,0][/math].

Шаг	Строка	Значение функции
[math]1[/math]	a	0
[math]2[/math]	ab	0
[math]3[/math]	abc	0
[math]4[/math]	abca	1
[math]5[/math]	abcab	2
[math]6[/math]	abcabc	3
[math]7[/math]	abcabcd	0

Время работы

Всего [math]O(n^2)[/math] итераций цикла, на каждой из который происходит сравнение строк за [math]O(n)[/math], что дает в итоге [math]O(n^3)[/math].

Оптимизация

Вносятся несколько важных замечаний:

• Следует заметить, что [math]\pi(i) \le \pi(i-1) + 1[/math]. По определению префикс функции верно, что [math]s[1..\pi(i)] = s[i - \pi(i) + 1..i][/math]. В частности, получается, что [math]s[1..\pi(i) - 1] = s[i - \pi(i) + 1..i - 1][/math]. Поскольку [math]\pi[/math] это наибольший префикс равный суффиксу, то [math]\pi(i - 1) \ge \pi(i) - 1[/math].
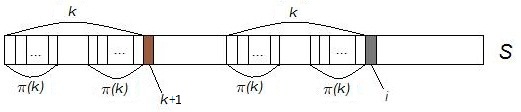
• Избавимся от явных сравнений строк. Для этого подберем такое [math]k[/math], что [math]k = \pi(i) - 1[/math]. Делаем это следующим образом. За исходное [math]k[/math] необходимо взять [math]\pi(i - 1)[/math], что следует из первого пункта. В случае, когда символы [math]s[k+1][/math] и [math]s[i][/math] не совпадают, [math]\pi(k)[/math] — следующее потенциальное наибольшее значение [math]k[/math], что видно из рисунка. Последнее утверждение верно, пока [math]k\gt 0[/math], что позволит всегда найти его следующее значение. Если [math]k=0[/math], то [math]\pi(i)=1[/math] при [math]s[i] = s[1][/math] , иначе [math]\pi(i)=0[/math].

Псевдокод

Prefix_function ([math]s[/math])
     [math]\pi[/math][1] = 0
     k = 0
     for i = 2 to n
         while k > 0 && s[i] != s[k + 1]
             k = [math]\pi[/math][k]
         if s[i] == s[k + 1]
             k++
         [math]\pi[/math][i] = k
     return [math]\pi[/math]

Время работы

Время работы алгоритма составит [math]O(n)[/math]. Для доказательства этого нужно заметить, что итоговое количество итераций цикла [math]while[/math] определяет асимптотику алгоритма. Теперь стоит отметить, что [math]k[/math] увеличивается на каждом шаге не более чем на единицу, значит максимально возможное значение [math]k = n - 1[/math]. Поскольку внутри цикла [math]while[/math] значение [math]k[/math] лишь уменьшается, получается, что [math]k[/math] не может суммарно уменьшиться больше, чем [math]n-1[/math] раз. Значит цикл [math]while[/math] в итоге выполнится не более [math]n[/math] раз, что дает итоговую оценку времени алгоритма [math]O(n)[/math].

Построение строки по префикс-функции

Постановка задачи

Восстановить строку по префикс-функции за [math]O(N)[/math] (алфавит неограничен).

Описание алгоритма

В дальнейшем нумерация символов в строках будет с [math]1[/math].

Пусть в массиве [math]p[/math] хранятся значения префикс-функции, в [math]s[/math] будет записан ответ. Пойдем по массиву [math]p[/math] слева направо. Пусть мы хотим узнать значение [math]s[i][/math], посмотрим на значение [math]p[i][/math], если [math]p[i] =0[/math] тогда в [math]s[i][/math] запишем новый символ, иначе [math]s[i] = s[p[i]][/math]. Обратим внимание, что [math]s[p[i]][/math] мы посчитали раньше, так как [math]p[i] \lt i[/math]. Так как подстрока с [math]1[/math] по [math]p[i][/math] заканчивается в [math]s[i][/math], то [math]s[i][/math] должен быть равен [math]s[p[i]][/math].

Псевдокод

string buildFromPrefix(int[] p) 
for i = 0 to p.length - 1
    if p[i] == 0     
          s += new char
    else
          s += s[p[i]]
return s

Доказательство корректности алгоритма

Докажем, что если нам дали корректную префикс-функцию, то наш алгоритм построит строку с такой же префикс-функцией. Также заметим, что строк с такой префикс-функцией может быть много, и алгоритм строит только одну из них.

Пусть [math]p[/math] данная префикс-функция, [math]s'[/math] правильная строка, [math]s[/math] эту строку построил наш алгоритм, [math] q [/math] массив значений префикс-функции для [math]s[/math].

Докажем корректность индукцией по длине массива префикс-функции полученной строки.

База очевидна для строки длиной [math]1[/math].

Переход: Пусть до [math]n[/math]-ой позиции мы построили строку, что [math]p[1..n - 1] = q[1..n - 1][/math]. Возможно два варианта,

[math]1)[/math] [math]p[n] = 0[/math]. Тогда мы добавляем новый символ, поэтому [math]q[n][/math] тоже будет равно [math]0[/math]. Также, предыдущие значения [math]q[/math] не поменяются и останутся верными.

[math]2)[/math] [math]p[n] \gt 0[/math]. Предположим, что [math]q[n] \neq p[n] [/math]. Заметим, что подстрока с [math]1[/math] по [math]p[n][/math] оканчивается на [math]n[/math]-ом символе. По предположению индукции наш алгоритм построил правильную строку до [math]n - 1[/math] символа, следовательно, [math]p[n] \leqslant q[n][/math]. Представим, что [math]q[n] \gt p[n] [/math], тогда получается, что префикс с [math]1..q[n][/math] в строке [math]s'[/math], является подстрокой заканчивающийся на [math]n[/math]-ом символе, но тогда возникает противоречие с тем, что массив [math]p[/math] корректный

Простой пример некорректного [math]p = {0,1,1} [/math], тогда по алгоритму получится строка [math]aaa[/math]. Очевидно, что префикс-функции не будут совпадать.

Литература

Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296.