Алгоритм Фараха

Эта статья находится в разработке!

Алгоритм Фарача — алгоритм построения суффиксного дерева для заданной строки [math]s[/math], который выполняется за время [math]O(N)[/math], при этом даже не требуется выполнения условия конечности алфавита. Такая эффективность достигается за счет того, что строковые последовательности определяются на индексированном алфавите или, что эквивалентно, на целочисленном алфавите [math]\Sigma = \{1, 2 {...}, a\}[/math], при этом накладывается дополнительное условие, что [math]a \in O(N)[/math]. Такие алфавиты часто встречаются на практике.

описание алгоритма

Основная идея алгоритма, заключается в том что мы уменьшаем размер исходной строки. Для этого мы разбиваем символы сходной строки на пару и пронумеровываем их, а из полученных номеров составляем новую строку, которая уже в 2 раза короче.

Мы опишем алгоритм Фарача в виде пяти выполняемых шагов. Используем в качестве примера строку [math]s = 121112212221[/math], определенную на алфавите [math]А = {1, 2} [/math] (в этом примере N = 12).

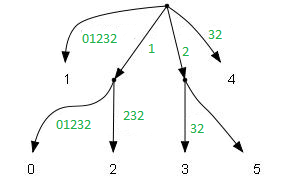
шаг 0: суффиксное дерево для сжатой строки

* Строка [math]s[/math] разбивается на пары: [math] 12 11 12 21 22 21 [/math]
* Пары сортирутся поразрядной сортировкой: [math]11 12 12 21 21 22 [/math].
* Удаляются копии: [math]11 12 21 22[/math].
* Парам даются номера (условно, в массиве они и так есть): [math]11-(0), 12-(1), 21-(2), 22-(3)[/math]
* Создаётся новая строка из номеров пар: 1 0 1 2 3 2
* Из полученной строки создаётся суффикcное дерево:

суфдерево для сжатой строки

ID	LCP	STR
1	0	0 1 2 3 2
0	0	1 0 1 2 3 2
2	1	1 2 3 2
3	0	2 3 2
5	1	2
4	0	3 2

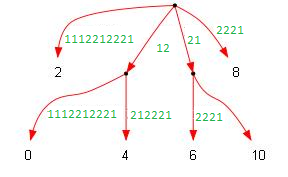
шаг 1: построение четного дерева

Определение:

Четное дерево [math]T^{even}_s[/math] является деревом суффиксов для строки [math]s[/math], узлы-листья которого ограничены нечетными позициями [math]2,4,6,{...} [/math] строки [math]s\$[/math].

Из дерева сжатой строки получаем частичное (чётное) дерево исходной строки. Частичное потому в нём будут только половина суффиксов, т.е. тех которые стоят в чётных позициях. :

Очевидно, что для этого достаточно умножить все расстояния в дереве на 2

Корректируются все развилки дерева (так как они могут совпадать в первых символах)

ID	LCP	STR
2	0	1112212221
0	1	121112212221
4	2	12212221
6	0	212221
10	2	21
8	1	2221

шаг 2: построение нечетного по четному

Определение:

Нечетное дерево [math]T^{odd}_s[/math] является деревом суффиксов для строки [math]s[/math], узлы-листья которого ограничены нечетными позициями [math]1,3,5,{...} [/math] строки [math]s\$[/math].

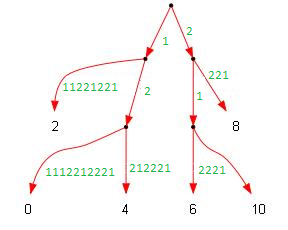
шаг 3: слияние четного и нечетного дерева

Далее необходимо найти эффективный способ слияния нечетного и четного деревьев в одно дерево [math]Т_s[/math]. Слияние будем производить начиная с корня. Предположим, что для каждого узла деревьев [math]Т_s^{odd}[/math] и [math]Т_s^{even}[/math] выходящие из них ребра занесены в специальные списки, где они упорядочены в возрастающем лексикографическом порядке подстрок, которые представляют эти ребра. Алгоритм слияния деревьев просматривает только первые буквы подстрок, представленных ребрами деревьев [math]Т_s^{odd}[/math] и [math]Т_s^{even}[/math], пусть это будут буквы [math]\lambda^{odd}[/math] и [math]\lambda^{even}[/math]. Тогда:

• если [math]\lambda^{odd}[/math] [math]\ne[/math] [math]\lambda^{even}[/math], определяется поддерево, соответствующее меньшей из этих букв, и без изменений присоединяется к узлу-родителю;
• если [math]\lambda^{odd}[/math] [math]=[/math] [math]\lambda^{even}[/math] и длины подстрок, представленных соответствующими ребрами, равны, в дерево слияния к текущему узлу добавляются два сына: один — из четного дерева, другой — из нечетного;
• если [math]\lambda^{odd}[/math] [math]=[/math] [math]\lambda^{even}[/math] и длины подстрок, представленных соответствующими ребрами, различны, в дерево слияния к текущему узлу добавляются два узла, находящиеся на одном нисходящем пути, при этом ближайший узел будет соответствовать более короткой подстроке.

Если начать эту процедуру для корней нечетного и четного деревьев, далее она рекурсивно выполняется для корней всех поддеревьев, которые, возможно, уже содержат узлы из нечетного и четного деревьев, поскольку ранее мог быть реализован случай [math]\lambda^{odd}[/math] [math]=[/math] [math]\lambda^{even}[/math]. Так как время манипулирования с любым ребром этих деревьев фиксированно, то общее время слияния деревьев составит [math]O(N)[/math].

В результате описанных действий получится дерево [math]M_x[/math],в котором будут присутствовать поддеревья, которые прошли процедуру сличния, и которые ее избежали (т.е были перенесены в дерево [math]M_x[/math] без изменений).