Целочисленный двоичный поиск — различия между версиями
Alex700 (обсуждение | вклад) |
Alex700 (обсуждение | вклад) |
||
| Строка 33: | Строка 33: | ||
== Код == | == Код == | ||
| − | <pre>binSearch(l, r) | + | <pre>binSearch(l, r) // l, r - левая и правая границы |
while l < r - 1 // запускаем цикл | while l < r - 1 // запускаем цикл | ||
m = (l + r) / 2; // m - середина области поиска | m = (l + r) / 2; // m - середина области поиска | ||
| Строка 44: | Строка 44: | ||
Инвариант цикла: пусть левый индекс меньше или равен искомого элемента, а правый {{---}} строго больше, тогда если <tex>l = r - 1</tex>, то понятно, что <tex>l</tex> {{---}} самое правое вхождение (так как следующее уже больше). | Инвариант цикла: пусть левый индекс меньше или равен искомого элемента, а правый {{---}} строго больше, тогда если <tex>l = r - 1</tex>, то понятно, что <tex>l</tex> {{---}} самое правое вхождение (так как следующее уже больше). | ||
| + | |||
| + | == См. также == | ||
| + | * [[Вещественный_двоичный_поиск|Вещественный двоичный поиск]] | ||
| + | * [[Троичный_поиск|Троичный поиск]] | ||
| + | * [[Поиск_с_помощью_золотого_сечения|Поиск с помощью золотого сечения]] | ||
| + | * [[Интерполяционный_поиск|Интерполяционный поиск]] | ||
== Источники == | == Источники == | ||
Версия 23:28, 22 мая 2014
| Определение: |
| Целочисленный двоичный поиск (бин. поиск) (от англ. Binary Search) — алгоритм поиска объекта по заданному признаку во множестве объектов, упорядоченных по тому же самому признаку. |
Содержание
Формулировка задачи
Пусть нам дан упорядоченный массив, состоящий только из целочисленных элементов. Нам надо найти в нём индекс, по которому находится искомый элемент, или же мы можем находить интервалы вхождения искомого элемента. Для этой задачи мы и можем использовать двоичный поиск.
Принцип работы
Двоичный поиск заключается в том, что на каждом шаге множество объектов делится на две части и в работе остаётся та часть множества, где находится искомый объект. Или же, в зависимости от постановки задачи, мы можем остановить процесс, когда мы получим первый или же последний индекс вхождения элемента. Последнее условие — это левосторонний/правосторонний двоичный поиск.
Правосторонний/левосторонний целочисленный двоичный поиск
Когда мы ищем правосторонним бинарным поиском, то он возвращает индекс самого правого вхождения заданного значения .
Когда же поиск левосторонний, возвращается индекс самого левого вхождения заданного значения .
Это разделение помогает находить количество подряд идущих равных значений.
Например:
Задан отсортированный массив
Правосторонний поиск двойки выдаст в результате , в то время как левосторонний выдаст .
От сюда следует, что количество подряд идущих двоек равно длине отрезка , то есть .
Если искомого элемента в массиве нет, то правосторонний поиск выдаст минимальный элемент, больший искомого, а левосторонний наоборот, максимальный элемент, меньший искомого.
Алгоритм двоичного поиска
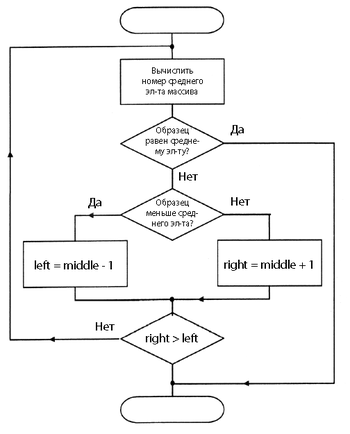
Идея поиска заключается в том, чтобы брать элемент посередине, между границами, и сравнивать его с искомым. В случае равенства возвращать его, а если искомое больше(в случае правостороннего — не меньше), чем элемент сравнения, то сужаем область поиска так, чтобы новая левая граница была равна индексу середины предыдущей области. В противном случае присваиваем это значение правой границе. Проделываем эту процедуру до тех пор, пока правая граница больше левой более чем на , или же пока мы не найдём искомый индекс.
Код
binSearch(l, r) // l, r - левая и правая границы
while l < r - 1 // запускаем цикл
m = (l + r) / 2; // m - середина области поиска
if a[m] < k
l = m;
else
r = m; // сужение границ
В случае правостороннего поиска изменится знак сравнения при сужении границ на ().
Инвариант цикла: пусть левый индекс меньше или равен искомого элемента, а правый — строго больше, тогда если , то понятно, что — самое правое вхождение (так как следующее уже больше).
См. также
Источники
- Д. Кнут - Искусство программирования (Том 3, 2-е издание)