Link-Cut Tree — различия между версиями
Lena (обсуждение | вклад) (→Оценка времени работы) |
Martoon (обсуждение | вклад) м |
||
| Строка 6: | Строка 6: | ||
==Решение задачи в частном случае== | ==Решение задачи в частном случае== | ||
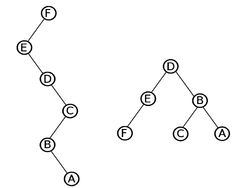
| − | Сначала научимся выполнять эти операции для частного случая, в котором все деревья - это пути. Для этого представим путь в виде splay-дерева, в | + | Сначала научимся выполнять эти операции для частного случая, в котором все деревья - это пути. Для этого представим путь в виде splay-дерева, в котором ключи выбираются равными глубине вершины. [[Файл:Path_to_tree.png|250px|thumb|right|Пример построения дерева для пути]] |
| − | Тогда операциям link и cut будут | + | Тогда операциям link и cut будут соответствовать merge и split. |
| − | Чтобы прибавлять заданное число на пути от вершины до корня, будем в каждой вершине хранить | + | Чтобы прибавлять заданное число на пути от вершины до корня, будем в каждой вершине хранить величину <tex>\Delta w</tex>, которая равна разнице между весом вершины и весом её родителя. Для корня это значение равно весу самого корня. Поэтому вес вершины определятся следующим образом: |
сумма | сумма | ||
| − | При прибавлении <tex>\alpha</tex> на пути от вершины <tex>v</tex> до корня, сначала | + | При прибавлении <tex>\alpha</tex> на пути от вершины <tex>v</tex> до корня, сначала вызывается <tex>splay(v)</tex>, после чего в левом поддереве находятся вершины, которые лежат на пути к корню. Затем надо прибавить <tex>\alpha</tex> к <tex>\Delta w(v)</tex> и, чтобы сохранить веса вершин, которые находятся ниже в пути, вычесть <tex>\alpha</tex> от <tex>\Delta w(v.right)</tex>. |
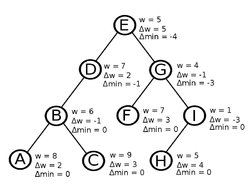
[[Файл:Linkcut_weights.png|250px|thumb|right|]] | [[Файл:Linkcut_weights.png|250px|thumb|right|]] | ||
Для поиска минимума поступим аналогично. Определим <tex>\Delta min(v)</tex> таким образом, чтобы сохранялся следующий инвариант: <tex>min(v) = \Delta min(v) + w(v) </tex>. Пусть <tex>l</tex> и <tex>r</tex> дети <tex>v</tex>, тогда | Для поиска минимума поступим аналогично. Определим <tex>\Delta min(v)</tex> таким образом, чтобы сохранялся следующий инвариант: <tex>min(v) = \Delta min(v) + w(v) </tex>. Пусть <tex>l</tex> и <tex>r</tex> дети <tex>v</tex>, тогда | ||
| − | <tex>min(v) = min\{w(v), min(l), min(r)\}</tex> | + | <tex>min(v) = min\{w(v), \ min(l), \ min(r)\}</tex> |
<tex>\Delta min(v) = min(v) - w(v) \\ | <tex>\Delta min(v) = min(v) - w(v) \\ | ||
| − | = min\{w(v) - w(v), min(l) - w(v), min(r) - w(v)\} \\ | + | = min\{w(v) - w(v), \ min(l) - w(v), \ min(r) - w(v)\} \\ |
| − | = min\{0, (\Delta min(l) + w(l)) - w(v), (\Delta min(r) + w(r)) - w(v)\} \\ | + | = min\{0, \ (\Delta min(l) + w(l)) - w(v), \ (\Delta min(r) + w(r)) - w(v)\} \\ |
| − | = min\{0, \Delta min(l) + \Delta w(l), \Delta min(r) + \Delta w(r)\}</tex> | + | = min\{0, \ \Delta min(l) + \Delta w(l), \ \Delta min(r) + \Delta w(r)\}</tex> |
Чтобы найти минимум на пути, надо вызвать <tex>splay(v)</tex>, а затем сравнить минимум <tex>v</tex> и минимум её левого ребенка. | Чтобы найти минимум на пути, надо вызвать <tex>splay(v)</tex>, а затем сравнить минимум <tex>v</tex> и минимум её левого ребенка. | ||
==Link-cut tree== | ==Link-cut tree== | ||
| − | Чтобы обобщить, | + | Чтобы обобщить, разобьем дерево на множество непересекающихся путей. Каждое ребро обозначим либо solid-ребром, либо dashed-ребром. Все пути в представляемом дереве хранятся в виде splay-деревьев. Корень каждого splay-дерева хранит указатель на вершину-родителя. |
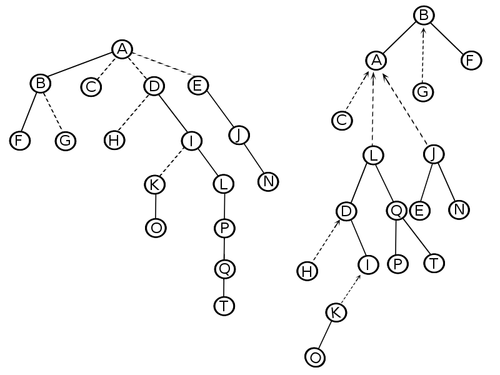
[[Файл:Linkcut_paths.png|500px||center|Разбиение дерева на пути]] | [[Файл:Linkcut_paths.png|500px||center|Разбиение дерева на пути]] | ||
| Строка 43: | Строка 43: | ||
parent(right(p)) <- null //поэтому правое поддерево p делаем новым путем | parent(right(p)) <- null //поэтому правое поддерево p делаем новым путем | ||
pathparent(right(p)) <- p | pathparent(right(p)) <- p | ||
| − | right(p) <- v // | + | right(p) <- v //объединяем оставшийся и построенный пути |
Δw(v) -= Δw(p) | Δw(v) -= Δw(p) | ||
Δmin(p) = min{0, Δmin(left(p)) + Δw(left(p)), Δmin(right(p)) + Δw(right(p))} | Δmin(p) = min{0, Δmin(left(p)) + Δw(left(p)), Δmin(right(p)) + Δw(right(p))} | ||
| Строка 79: | Строка 79: | ||
===cut(v)=== | ===cut(v)=== | ||
| − | Отрезает дерево с корнем <tex>v</tex>. После вызова <tex>expose(v) | + | Отрезает дерево с корнем <tex>v</tex>. После вызова <tex>expose(v) \ v</tex> станет корнем splay-дерева, и в правом поддереве будут содержатся все вершины, которые были ниже <tex>v</tex> в представляемом дереве, а в левом - те что выше. Обнулив указатель на левого ребенка <tex>v</tex> и на родителя в левом поддереве, получим требуемое. |
cut(v) | cut(v) | ||
| Строка 89: | Строка 89: | ||
==Оценка времени работы== | ==Оценка времени работы== | ||
| − | Назовем ребро из <tex>u</tex> в её родителя <tex>v</tex> тяжелым, если количество детей <tex>u</tex> <tex>d(u) > 1 | + | Назовем ребро из <tex>u</tex> в её родителя <tex>v</tex> тяжелым, если количество детей <tex>u</tex> <tex>d(u) > \frac{1}{2} d(v)</tex>. |
Лемма. Каждая вершина имеет не более одного тяжелого ребра | Лемма. Каждая вершина имеет не более одного тяжелого ребра | ||
| Строка 96: | Строка 96: | ||
M = |{все ребра, преобразованные из dashed в solid}| = |{легкие dashed-ребра, преобразованные в solid}| + |{тяжелые dashed-ребра, преобразованные в solid}| | M = |{все ребра, преобразованные из dashed в solid}| = |{легкие dashed-ребра, преобразованные в solid}| + |{тяжелые dashed-ребра, преобразованные в solid}| | ||
| − | По лемме, количество легких <tex>dashed</tex>-ребер, преобразованных в <tex>solid</tex>, будет не больше, чем <tex>log | + | По лемме, количество легких <tex>dashed</tex>-ребер, преобразованных в <tex>solid</tex>, будет не больше, чем <tex>\log n</tex>. |
| − | Обозначим за <tex>F</tex> лес деревьев, в которых каждое ребро либо solid, либо dashed, a <tex>F'</tex> - лес, получившийся из <tex>F</tex> после одного вызова <tex>expose</tex>. Определим потенциал <tex>\Phi _{a}(F) = n - 1 - |\{heavy solid-edges\}|</tex>. Пусть <tex>H</tex> - множество всех тяжелых ребер, <tex>L</tex> - все легкие ребра, <tex>S | + | Обозначим за <tex>F</tex> лес деревьев, в которых каждое ребро либо solid, либо dashed, a <tex>F'</tex> - лес, получившийся из <tex>F</tex> после одного вызова <tex>expose</tex>. Определим потенциал <tex>\Phi _{a}(F) = n - 1 - |\{heavy solid-edges\}|</tex>. Пусть <tex>H</tex> - множество всех тяжелых ребер, <tex>L</tex> - все легкие ребра, <tex>S \rightarrow D</tex> - множество solid-ребер, преобразованных в dashed в течение одного <tex>expose</tex>, <tex>D \rightarrow S</tex> - множество dashed-ребер, преобразованных в solid, <tex>\Delta \Phi _{a}</tex> - увеличение <tex>\Phi _{a}</tex> после одной операции <tex>expose</tex>. |
| − | Лемма2. <tex>V = M + \Delta \Phi _{a}<= 1 + | + | Лемма2. <tex>V = M + \Delta \Phi _{a}<= 1 + 2\log n </tex> |
<tex>V = M + \Delta \Phi _{a}\\ | <tex>V = M + \Delta \Phi _{a}\\ | ||
| − | = M + |H \cap S | + | = M + |H \cap S \rightarrow D| - |H \cap D \rightarrow S| \\ |
| − | \leqslant M + |L \cap D | + | \leqslant M + |L \cap D \rightarrow S| - |H \cap D \rightarrow S| \\ |
| − | = 2 * |L \cap D | + | = 2 * |L \cap D \rightarrow S| \\ |
| − | =2 * log | + | =2 * \log n |
</tex> | </tex> | ||
| − | Теперь проанализируем <tex>M</tex>. Используя тот факт, что начальное значение <tex>\Phi _{a}</tex> не превосходит <tex>n - 1</tex>, приходим к тому, что для деревьев с <tex>n</tex> вершинами, по крайней мере за <tex>n - 1</tex> операцию <tex>expose</tex>, среднее <tex>M</tex> на одну операцию будет не больше, чем <tex>1 + | + | Теперь проанализируем <tex>M</tex>. Используя тот факт, что начальное значение <tex>\Phi _{a}</tex> не превосходит <tex>n - 1</tex>, приходим к тому, что для деревьев с <tex>n</tex> вершинами, по крайней мере за <tex>n - 1</tex> операцию <tex>expose</tex>, среднее <tex>M</tex> на одну операцию будет не больше, чем <tex>1 + 2\log n</tex> |
Докажем, что амортизационная стоимость операции изменения класса ребер в link-cut-дереве равна <tex>O(1)</tex> | Докажем, что амортизационная стоимость операции изменения класса ребер в link-cut-дереве равна <tex>O(1)</tex> | ||
| − | Пусть </tex>s(v)</tex> - количество вершин в поддеревьях <tex>v</tex>(здесь имеется в виду splay-дерево T пути, котоый строится в ходе выполнения <tex>expose</tex>). <tex>\Phi = \sum_{v} log(s(v))</tex>. Нам известно, что стоимость i-той операции splay не превосходит 1 + 3*(r'(v_{i} - r(v_{i})). После каждого <tex>splay(v)</tex> v соединена с w = pathparent(v), поэтому s(w) > s(v). Это приводит к тому, что амортизационная стоимость <tex>expose</tex> ограничена следующим значением | + | Пусть </tex>s(v)</tex> - количество вершин в поддеревьях <tex>v</tex>(здесь имеется в виду splay-дерево T пути, котоый строится в ходе выполнения <tex>expose</tex>). <tex>\Phi = \sum_{v} \log (s(v))</tex>. Нам известно, что стоимость i-той операции splay не превосходит 1 + 3*(r'(v_{i} - r(v_{i})). После каждого <tex>splay(v)</tex> v соединена с w = pathparent(v), поэтому s(w) > s(v). Это приводит к тому, что амортизационная стоимость <tex>expose</tex> ограничена следующим значением |
| − | <tex>3 * log | + | <tex>3 * \log n - 3*\log (s(v)) + M</tex> |
| − | Здесь <tex>M = O(log | + | Здесь <tex>M = O(\log n)</tex>, поэтому амортизационная стоимость <tex>expose</tex> равна <tex>O(\log n)</tex> |
Версия 03:49, 10 июня 2014
Link-cut tree — это структура данных, которая хранит лес деревьев и позволяет выполнять следующие операции:
- искать минимум на пути от вершины до корня;
- прибавлять константу на пути от вершины до корня;
- link(u,w) -- подвешивать одно дерево на другое;
- cut(v) -- отрезать дерево с корнем в вершине v.
Содержание
Решение задачи в частном случае
Сначала научимся выполнять эти операции для частного случая, в котором все деревья - это пути. Для этого представим путь в виде splay-дерева, в котором ключи выбираются равными глубине вершины.Тогда операциям link и cut будут соответствовать merge и split.
Чтобы прибавлять заданное число на пути от вершины до корня, будем в каждой вершине хранить величину , которая равна разнице между весом вершины и весом её родителя. Для корня это значение равно весу самого корня. Поэтому вес вершины определятся следующим образом:
сумма
При прибавлении на пути от вершины до корня, сначала вызывается , после чего в левом поддереве находятся вершины, которые лежат на пути к корню. Затем надо прибавить к и, чтобы сохранить веса вершин, которые находятся ниже в пути, вычесть от .
Для поиска минимума поступим аналогично. Определим таким образом, чтобы сохранялся следующий инвариант: . Пусть и дети , тогда
Чтобы найти минимум на пути, надо вызвать , а затем сравнить минимум и минимум её левого ребенка.
Link-cut tree
Чтобы обобщить, разобьем дерево на множество непересекающихся путей. Каждое ребро обозначим либо solid-ребром, либо dashed-ребром. Все пути в представляемом дереве хранятся в виде splay-деревьев. Корень каждого splay-дерева хранит указатель на вершину-родителя.
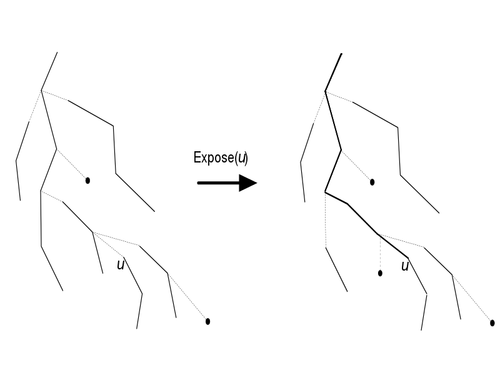
expose(u)
Ключевая операция в link-cut-деревьях — . После её выполнения лежит на одном пути с корнем представляемого дерева и при этом становится корнем в splay-дереве получившегося пути.
expose(u)
splay(u)
v <- u
while (v != root)
p <- pathparent(v) //получаем указатель на ближайшую вершину пути, пересекающего путь от u до корня
splay(p) //теперь в правом поддереве p находятся вершины пути, которые находятся ниже чем p в link-cut-дереве,
parent(right(p)) <- null //поэтому правое поддерево p делаем новым путем
pathparent(right(p)) <- p
right(p) <- v //объединяем оставшийся и построенный пути
Δw(v) -= Δw(p)
Δmin(p) = min{0, Δmin(left(p)) + Δw(left(p)), Δmin(right(p)) + Δw(right(p))}
pathparent(v) <- null
v <- p
splay(u)
add(v, c)
Чтобы прибавить константу на пути от до корня link-cut-дерева вызовем , что построит запрашиваемый путь в виде splay-дерева, в котором - корень, и в левом поддереве находятся вершины, которые находятся выше чем в link-cut-дереве (то есть все вершины пути без ), а в правом - те, что ниже. Тогда прибавим к и вычтем константу от правого ребенка , чтобы скомпенсировать разницу и сохранить инвариант.
add(v, c)
expose(v)
Δw(v) += c
Δw(right(v)) -= c
min(v)
Построим splay-дерево для пути и сравним минимум корня c минимумом в левом поддереве:
min(v)
expose(v)
if (Δmin(left(v)) + Δw(left(v)) < Δw(v))
then
return Δmin(left(v)) + Δw(left(v))
else
return Δw(v)
link(v, u)
Если - корень, а - вершина в другом дереве, то соединяет два дерева добавлением ребра , причем становится родителем .
link(v, u)
expose(v) //теперь v - корень в splay-дереве пути и не имеет левого ребенка(так как ключ равен глубине в представляемом дереве)
expose(u)
Δw(u) -= Δw(v) //чтобы сделать u родителем v в представляемом дереве 1. делаем путь, содержащий u, левым ребенком v в splay-дереве
parent(u) = v // 2. обновляем Δw, Δmin
left(v) = u
Δmin(v) = min{0, Δmin(u) + Δw(u), Δmin(right(v)) + Δw((right(v)))}
cut(v)
Отрезает дерево с корнем . После вызова станет корнем splay-дерева, и в правом поддереве будут содержатся все вершины, которые были ниже в представляемом дереве, а в левом - те что выше. Обнулив указатель на левого ребенка и на родителя в левом поддереве, получим требуемое.
cut(v)
expose(v)
Δw(left(v)) += Δw(v)
Δmin(v) = min{0, Δmin(right(v)) + Δw(right(v))}
left(v) = null
parent(left(v)) = null
Оценка времени работы
Назовем ребро из в её родителя тяжелым, если количество детей . Лемма. Каждая вершина имеет не более одного тяжелого ребра
Операция осуществляется с помощью последовательности преобразований dashed-ребра в solid-ребро и другого solid-ребра в dashed-ребро. Обозначим количество таких преобразований за . Найдем количество таких преобразований сделанных в течение .
M = |{все ребра, преобразованные из dashed в solid}| = |{легкие dashed-ребра, преобразованные в solid}| + |{тяжелые dashed-ребра, преобразованные в solid}|
По лемме, количество легких -ребер, преобразованных в , будет не больше, чем .
Обозначим за лес деревьев, в которых каждое ребро либо solid, либо dashed, a - лес, получившийся из после одного вызова . Определим потенциал . Пусть - множество всех тяжелых ребер, - все легкие ребра, - множество solid-ребер, преобразованных в dashed в течение одного , - множество dashed-ребер, преобразованных в solid, - увеличение после одной операции .
Лемма2.
Теперь проанализируем . Используя тот факт, что начальное значение не превосходит , приходим к тому, что для деревьев с вершинами, по крайней мере за операцию , среднее на одну операцию будет не больше, чем
Докажем, что амортизационная стоимость операции изменения класса ребер в link-cut-дереве равна
Пусть </tex>s(v)</tex> - количество вершин в поддеревьях (здесь имеется в виду splay-дерево T пути, котоый строится в ходе выполнения ). . Нам известно, что стоимость i-той операции splay не превосходит 1 + 3*(r'(v_{i} - r(v_{i})). После каждого v соединена с w = pathparent(v), поэтому s(w) > s(v). Это приводит к тому, что амортизационная стоимость ограничена следующим значением
Здесь , поэтому амортизационная стоимость равна