Straight skeleton — различия между версиями
Shersh (обсуждение | вклад) |
Shersh (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
{{В разработке}} | {{В разработке}} | ||
| − | + | Существует целый класс структур типа <tex>\mathrm{skeleton}</tex>, которые описывают базовые топологические свойства объектов. Структура <tex>\mathrm{straight}\ \mathrm{skeleton}</tex> была придумала Oswin Aichholzer<ref>[http://www.jucs.org/jucs_1_12/a_novel_type_of/Aichholzer_O.pdf A Novel Type of Skeleton for Polygons]</ref>. Она используются в различных практических задачах, а также для доказательства некоторых теорем<ref>[http://en.wikipedia.org/wiki/Fold-and-cut_theorem Fold-and-cut theorem]</ref>. | |
| + | == Топологические свойства == | ||
{{Определение | {{Определение | ||
|id=defss | |id=defss | ||
| − | |definition= | + | |definition='''Straight skeleton''' (Angular Bisector Network, ABN) полигона без самопересечений определяет разбиение полигона на регионы, границами которых являются стороны полигона, биссектрисы углов и отрезки, соединяющие точки пересечения биссектрис. |
}} | }} | ||
| + | [[Файл:Straight_skeleton_definition.png|right]] | ||
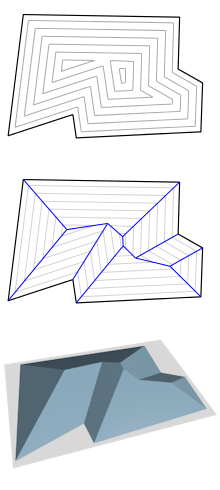
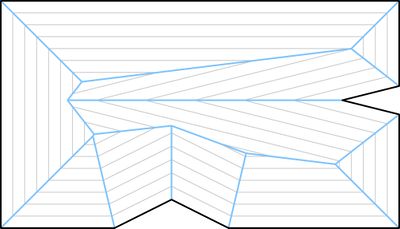
| + | Опишем подробней, как получается такое разбиение. Мы можем представить, будто все стороны прямоугольника параллельно двигаются внутрь с одинаковой постоянной скоростью. Тогда {{Acronym | вершины будут двигаться вдоль биссектрис | Очевидный факт}}, а точки пересечения биссектрис будут соединять совпавшие участки сторон прямоугольника в конце движения. В каждый момент времени от начала движения рёбер мы получаем слоистую структуру (рис 1.). Чем-то она похожа на строение крыши в домах (рис. 3). На рис. 2 синим цветом выделен <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> {{---}} множество отрезков, образованных точками пересечения при движении сторон полигона. | ||
| + | |||
| + | [[Файл:sk_example1.jpg|400px]] | ||
| + | |||
| + | == Свойства дерева Straigh skeleton == | ||
| + | {{TODO | t = Леммы о свойствах структуры Straight skeleton}} | ||
| + | |||
| + | == Wavefront-алгоритм == | ||
| + | {{TODO | t = Алгоритм построения простой за n^3 log n (wavefront)}} | ||
| + | |||
| + | == Для монотонных многоугольников == | ||
| + | {{TODO | t = Алгоритм для монотонных многоугольников за n log n}} | ||
| + | |||
| + | == Сложный алгоритм == | ||
| + | {{TODO | t = Алгоритм в общем виде за n*m + n log n}} | ||
| + | |||
| + | == Примечания == | ||
| + | <references /> | ||
== Источники информации == | == Источники информации == | ||
| + | * [http://en.wikipedia.org/wiki/Straight_skeleton Wikipedia {{---}} Straight skeleton] | ||
* [http://www.dma.fi.upm.es/mabellanas/tfcs/skeleton/html/documentacion/straight%20skeletons%20implementation.pdf Straight Skeleton Implementation] | * [http://www.dma.fi.upm.es/mabellanas/tfcs/skeleton/html/documentacion/straight%20skeletons%20implementation.pdf Straight Skeleton Implementation] | ||
* [http://www.sthu.org/research/publications/files/phdthesis.pdf Computing Straight Skeletons and Motorcycle Graphs: Theory and Practice] | * [http://www.sthu.org/research/publications/files/phdthesis.pdf Computing Straight Skeletons and Motorcycle Graphs: Theory and Practice] | ||
| + | * [https://liorpachter.wordpress.com/tag/straight-skeleton/ Designing roofs and drawing phylogenetic trees] | ||
[[Категория: Вычислительная геометрия]] | [[Категория: Вычислительная геометрия]] | ||
[[Категория: Скалярное произведение и мера]] | [[Категория: Скалярное произведение и мера]] | ||
[[Категория: Структуры данных]] | [[Категория: Структуры данных]] | ||
Версия 01:08, 16 сентября 2014
Существует целый класс структур типа , которые описывают базовые топологические свойства объектов. Структура была придумала Oswin Aichholzer[1]. Она используются в различных практических задачах, а также для доказательства некоторых теорем[2].
Содержание
Топологические свойства
| Определение: |
| Straight skeleton (Angular Bisector Network, ABN) полигона без самопересечений определяет разбиение полигона на регионы, границами которых являются стороны полигона, биссектрисы углов и отрезки, соединяющие точки пересечения биссектрис. |
Опишем подробней, как получается такое разбиение. Мы можем представить, будто все стороны прямоугольника параллельно двигаются внутрь с одинаковой постоянной скоростью. Тогда вершины будут двигаться вдоль биссектрис , а точки пересечения биссектрис будут соединять совпавшие участки сторон прямоугольника в конце движения. В каждый момент времени от начала движения рёбер мы получаем слоистую структуру (рис 1.). Чем-то она похожа на строение крыши в домах (рис. 3). На рис. 2 синим цветом выделен — множество отрезков, образованных точками пересечения при движении сторон полигона.
Свойства дерева Straigh skeleton
TODO: Леммы о свойствах структуры Straight skeleton
Wavefront-алгоритм
TODO: Алгоритм построения простой за n^3 log n (wavefront)
Для монотонных многоугольников
TODO: Алгоритм для монотонных многоугольников за n log n
Сложный алгоритм
TODO: Алгоритм в общем виде за n*m + n log n