Обсуждение участника:NikitaMarkovnikov — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(Новая страница: «{{Теорема |id = Th1 |about = о близких запросах в сплей-дереве |statement = Пусть в сплей-дерево слож...»)
 
 
(не показаны 2 промежуточные версии этого же участника)
Строка 2: Строка 2:
 
|id = Th1  
 
|id = Th1  
 
|about =  
 
|about =  
−
о близких запросах в сплей-дереве
+
Поша
  
−
|statement =  
+
|statement = Пусть граф <tex> G </tex> имеет <tex>n \geqslant 3</tex> вершин.
−
Пусть в сплей-дерево сложены ключи <tex> 1, \dotsc, n </tex>, зафиксируем один из ключей <tex> f </tex>, пусть выполняется <tex> m </tex> запросов к ключам. Тогда суммарное время на запросы есть <tex> \displaystyle O(n \log_{2} n + m + \sum_{i=1}^{m} \log_2 ( \lvert q_{i} - f \rvert + 1)) </tex>, где <tex> q_{i} </tex> {{---}} <tex> i </tex>-й запрос.
 
  
−
|proof =
+
*Если для всякого <tex>k,\, 1 \leqslant k < (n-1)/2</tex>, число вершин со степенями, не превосходящими <tex>k</tex>, меньше чем <tex>k</tex>, и
 +
*Если для нечетного <tex>n</tex> число вершин степени <tex>(n-1)/2</tex> не превосходит <tex>(n-1)/2</tex>,
  
−
Для доказательства теоремы воспользуемся методом потенциалов:
+
то <tex> G </tex> {{---}} [[Гамильтоновы графы|гамильтонов]] граф.
  
−
<tex> a_{i} = t_{i} + \Phi_{i} - \Phi_{i-1} </tex>  
+
|proof =
 +
Предположим, что теорема неверна. Пусть <tex> G </tex> {{---}} максимальный негамильтонов граф с <tex> n </tex> вершинами, удовлетворяющий условиям теоремы.
  
−
По условию выполняется <tex> m </tex> запросов, следовательно
+
Легко видеть, что добавление любого ребра в граф, обладающий указанными свойствами, приводит к графу, который также обладает этими свойствами. Таким образом, поскольку добавление к <tex> G </tex> произвольного ребра приводит к гамильтонову ребру, любые две несмежные вершины соединимы простой остовной цепью.
  
−
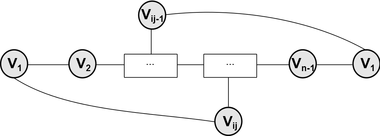
<tex> T = \displaystyle \sum_{i=1}^{m} t_{i} = \sum_{i=1}^{m} \left(a_{i} + \Phi_{i-1} - \Phi_{i} \right) = \sum_{i=1}^{m} a_{i} + \Phi_{0} - \Phi_{m} = \sum_{i=1}^{m} a_{i} + \Delta \Phi </tex> <tex> (\ast) </tex>
+
Покажем сначала, что всякая вершина, степень которой не меньше <tex> (n-1)/2 </tex>, смежна с каждой вершиной со степенью, большей чем <tex> (n-1)/2 </tex>. Не умаляя общности, допустим, что <tex> \deg v_{1} \geqslant (n-1)/2 </tex> и <tex> \deg v_{n} \geqslant n/2 </tex>, но вершины <tex> v_{1} </tex> и <tex> v_{n} </tex> не смежны. Тогда существует простая остовная цепь <tex> v_{1} v_{2} \dotsc v_{n} </tex>, соединяющая <tex> v_{1} </tex> и <tex> v_{n} </tex>. Обозначим вершины, смежные с <tex> v_{1} </tex>, через <tex> v_{{i}_{1}}, \dotsc,v_{{i}_{k}} </tex>, где <tex> k = \deg v_{1} </tex> и <tex> 2=i_{1} < i_{2} < \dotsc < i_{k} </tex>. [[Файл: Graph-Posha.png|380px|thumb|right|]] Ясно, что вершина <tex> v_{n} </tex> не может быть смежной ни с одной вершиной из <tex> G </tex> вида <tex> v_{{i}_{j-1}} </tex>, поскольку тогда в <tex> G </tex> был бы гамильтонов цикл <tex> v_{1} v_{2} \dotsc v_{{i}_{j-1}} v_{n} v_{n-1} \dotsc v_{{i}_{j}} v_{1} </tex>.
  
−
Для удобства введем обозначения:
+
Далее, так как <tex> k \geqslant (n-1)/2 </tex>, то <tex> n/2 \leqslant \deg v_{n} \leqslant n-1-k < n/2 </tex>, что невозможно. Поэтому <tex> v_{1} </tex> и <tex> v_{n} </tex> должны быть смежны.
  
−
# Весом узла с ключом <tex> q </tex> будем называть величину <tex> w(q) =\displaystyle \frac {1}{\left(\lvert q - f \rvert + 1 \right )^{2}} </tex>.
+
Отсюда следует, что если <tex> \deg v \geqslant n/2 </tex> для всех вершин <tex> v </tex>, то <tex> G </tex> {{---}} гамильтонов граф. В силу изложенного выше каждая пара вершин графа <tex> G </tex> смежна, т.е. <tex> G </tex> {{---}} полный граф. Мы пришли к противоречию, поскольку <tex> K_{n} </tex> {{---}} гамильтонов граф для всех <tex> n \geqslant 3 </tex>.
  
−
# Размером узла, содержащего ключ <tex> q </tex>, будем называть величину <tex> s(q) = \displaystyle \sum_{y} w(y) </tex>, где <tex> y </tex> {{---}} узлы поддерева с корнем в <tex> q </tex>.
+
Таким образом, в <tex> G </tex> есть вершина <tex> v </tex> с <tex> \deg v < n/2 </tex>. Обозначим через <tex> m </tex> наибольшую среди степеней всех таких вершин. Выберем такую вершину <tex> v_{1} </tex>, что <tex> \deg v_{1} = m </tex>. По принятому предположению число вершин со степенями, не превосходящими <tex> m </tex>, не больше чем <tex> m < n/2 </tex>, поэтому должно быть более чем <tex> m </tex> вершин со степенями, превосходящими <tex> m </tex>, и, следовательно, не меньшими чем <tex> n/2 </tex>. В результате найдется некоторая вершина, скажем <tex> v_{n} </tex>, степени по крайней мере <tex> n/2 </tex>, не смежная с <tex> v_{1} </tex>. Так как <tex> v_{1} </tex> и <tex> v_{n} </tex> не смежны, то существует остовная простая цепь <tex> v_{1} \dotsc v_{n} </tex>. Как и выше, обозначим через <tex> v_{{i}_{1}}, \dotsc, v_{{i}_{m}} </tex> вершины графа <tex> G </tex>, смежные с <tex> v_{1} </tex>, и заметим, что вершина <tex> v_{n} </tex> не может быть смежной ни с одной из <tex> m </tex> вершин <tex> v_{{i}_{j-1}} </tex> для <tex> 1 \leqslant j \leqslant m </tex>. Но поскольку <tex> v_{1} </tex> и <tex> v_{n} </tex> не смежны, а <tex> v_{n} </tex> имеет степень не меньше <tex> n/2 </tex>, то, как было показано в первой части доказательства, <tex> m </tex> должно быть меньше чем <tex> (n-1)/2 </tex>. Так как по предположению число вершин со степенями, не превосходящими <tex> m </tex>, меньше чем <tex> m </tex>, то хотя бы одна из <tex> m </tex> вершин <tex> v_{{i}_{j-1}} </tex>, скажем <tex> v' </tex>, должна иметь степень не меньше <tex> n/2 </tex>. Итак, мы установили, что степени двух несмежных вершин <tex> v_{n} </tex> и <tex> v' </tex> не меньше <tex> n/2 </tex>. Полученное противоречие завершает доказательство теоремы.
 +
}}
  
−
# <tex> r(q) = \log_{2}s(q) </tex> {{---}} ранг узла.
+
'''Замечания'''
  
−
# Потенциал дерева обозначим как <tex> \Phi = \displaystyle \sum_{q=1}^{n} r(q) = \displaystyle \sum_{q=1}^{n} \log_{2}s(q) </tex>.
+
*Приведенное достаточное условие не является необходимым.
 +
*Условия теоремы нельзя улучшить, так как при их ослаблении новое условие уже не будет достаточным для гамильтоновости графа.
  
−
Пусть <tex> W </tex> {{---}} вес дерева. Тогда <tex> W = \displaystyle \sum_{q=1}^{n} w(q) = \sum_{q=1}^{n} \frac {1}{\left(\lvert q - f \rvert + 1 \right)^{2}}  \leqslant 2 \cdot \sum_{q=1}^{+\infty} \frac {1}{ \left ( \lvert q - f \rvert + 1 \right)^{2}} = O(1) </tex>.
+
Ограничивая условия теоремы Поша, получаем более простые, но менее сильные достаточные условия, найденные Оре и Дираком соответственно:
  
−
Из определения размера узла следует, что <tex> w(q) \leqslant s(q) \leqslant W </tex>.
+
{{Теорема
 +
|id = Th2
 +
|about = Следствие 1
 +
|statement =
 +
Если <tex> n \geqslant 3 </tex> и <tex> \deg u + \deg v  \geqslant n </tex> для любой пары <tex> u </tex> и <tex> v </tex> несмежных вершин графа <tex> G </tex>, то <tex> G </tex> {{---}} гамильтонов граф.  
 +
}}
  
−
Также заметим, что для любого <tex> q </tex> от <tex> 1 </tex> до <tex> n </tex> верно <tex> w(q) \geqslant \displaystyle \frac {1}{n^{2}} </tex>.
+
{{Теорема
 +
|id = Th3
 +
|about = Следствие 2
 +
|statement =
 +
Если <tex> n > 3 </tex> и <tex> \deg v  \geqslant n/2 </tex> для любой вершины <tex> v </tex> графа <tex> G </tex>, то <tex> G </tex> {{---}} гамильтонов граф.  
 +
}}
  
−
Тогда изменение потенциала
+
==Источники==
−
 
+
*Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 60 с.
−
<tex> \Delta\Phi \leqslant \displaystyle \sum_{q=1}^{n} \log_{2} W - \sum_{q=1}^{n} \log_{2}w(q) = \sum_{q=1}^{n} \log_{2} \frac {W}{w(q)} = O \Biggl(\sum_{q=1}^{n} \log_{2} n^{2}\Biggr) = </tex> <tex> \displaystyle O\Biggl(2 \cdot\sum_{q=1}^{n} \log_{2} n\Biggr) = O\left(n \log_{2}n\right)  </tex>.
 
−
 
 
−
Обозначим за <tex> t </tex> корень сплей-дерева. Тогда, воспользовавшись вышеуказанной леммой, получаем, что
 
−
 
 
−
<tex> \displaystyle a_{i} = 3 \cdot \left( r(t) - r(q_{i}) \right) + 1 = O\left(\log_{2} \frac{s(t)}{s\left(q_{i}\right)}\right) + 1 = O\left(\log_{2} \frac{W}{w(q_{i})}\right) + 1 = </tex> <tex> O\left(\log_{2} \left(W \cdot \left(\lvert q - f \rvert + 1 \right)^{2} \right ) \right ) + 1 = O\left(\log_{2} \left(\lvert q - f \rvert + 1 \right) \right ) + 1  </tex>
 
−
 
 
−
Тогда, подставляя найденные значения в формулу <tex> (\ast) </tex>,  получаем, что
 
−
 
 
−
<tex>T=\displaystyle \sum_{i=1}^{m} \left ( O \left( \log_{2} \left ( \lvert q_{i} - f \rvert + 1 \right) \right) + 1 \right ) + O\left ( n \log_{2} n \right) = </tex> <tex> \displaystyle O \left (n \log_{2} n + m + \displaystyle \sum_{i=1}^{m} \log_2 \left( \lvert q_{i} - f \rvert + 1 \right) \right)</tex>
 
−
 
 
−
}}
 

Текущая версия на 22:18, 10 октября 2014

Теорема (Поша):
Пусть граф [math] G [/math] имеет [math]n \geqslant 3[/math] вершин.
  • Если для всякого [math]k,\, 1 \leqslant k \lt (n-1)/2[/math], число вершин со степенями, не превосходящими [math]k[/math], меньше чем [math]k[/math], и
  • Если для нечетного [math]n[/math] число вершин степени [math](n-1)/2[/math] не превосходит [math](n-1)/2[/math],
то [math] G [/math] — гамильтонов граф.
Доказательство:
[math]\triangleright[/math]

Предположим, что теорема неверна. Пусть [math] G [/math] — максимальный негамильтонов граф с [math] n [/math] вершинами, удовлетворяющий условиям теоремы.

Легко видеть, что добавление любого ребра в граф, обладающий указанными свойствами, приводит к графу, который также обладает этими свойствами. Таким образом, поскольку добавление к [math] G [/math] произвольного ребра приводит к гамильтонову ребру, любые две несмежные вершины соединимы простой остовной цепью.

Покажем сначала, что всякая вершина, степень которой не меньше [math] (n-1)/2 [/math], смежна с каждой вершиной со степенью, большей чем [math] (n-1)/2 [/math]. Не умаляя общности, допустим, что [math] \deg v_{1} \geqslant (n-1)/2 [/math] и [math] \deg v_{n} \geqslant n/2 [/math], но вершины [math] v_{1} [/math] и [math] v_{n} [/math] не смежны. Тогда существует простая остовная цепь [math] v_{1} v_{2} \dotsc v_{n} [/math], соединяющая [math] v_{1} [/math] и [math] v_{n} [/math]. Обозначим вершины, смежные с [math] v_{1} [/math], через [math] v_{{i}_{1}}, \dotsc,v_{{i}_{k}} [/math], где [math] k = \deg v_{1} [/math] и [math] 2=i_{1} \lt i_{2} \lt \dotsc \lt i_{k} [/math].
Graph-Posha.png
Ясно, что вершина [math] v_{n} [/math] не может быть смежной ни с одной вершиной из [math] G [/math] вида [math] v_{{i}_{j-1}} [/math], поскольку тогда в [math] G [/math] был бы гамильтонов цикл [math] v_{1} v_{2} \dotsc v_{{i}_{j-1}} v_{n} v_{n-1} \dotsc v_{{i}_{j}} v_{1} [/math].

Далее, так как [math] k \geqslant (n-1)/2 [/math], то [math] n/2 \leqslant \deg v_{n} \leqslant n-1-k \lt n/2 [/math], что невозможно. Поэтому [math] v_{1} [/math] и [math] v_{n} [/math] должны быть смежны.

Отсюда следует, что если [math] \deg v \geqslant n/2 [/math] для всех вершин [math] v [/math], то [math] G [/math] — гамильтонов граф. В силу изложенного выше каждая пара вершин графа [math] G [/math] смежна, т.е. [math] G [/math] — полный граф. Мы пришли к противоречию, поскольку [math] K_{n} [/math] — гамильтонов граф для всех [math] n \geqslant 3 [/math].

Таким образом, в [math] G [/math] есть вершина [math] v [/math] с [math] \deg v \lt n/2 [/math]. Обозначим через [math] m [/math] наибольшую среди степеней всех таких вершин. Выберем такую вершину [math] v_{1} [/math], что [math] \deg v_{1} = m [/math]. По принятому предположению число вершин со степенями, не превосходящими [math] m [/math], не больше чем [math] m \lt n/2 [/math], поэтому должно быть более чем [math] m [/math] вершин со степенями, превосходящими [math] m [/math], и, следовательно, не меньшими чем [math] n/2 [/math]. В результате найдется некоторая вершина, скажем [math] v_{n} [/math], степени по крайней мере [math] n/2 [/math], не смежная с [math] v_{1} [/math]. Так как [math] v_{1} [/math] и [math] v_{n} [/math] не смежны, то существует остовная простая цепь [math] v_{1} \dotsc v_{n} [/math]. Как и выше, обозначим через [math] v_{{i}_{1}}, \dotsc, v_{{i}_{m}} [/math] вершины графа [math] G [/math], смежные с [math] v_{1} [/math], и заметим, что вершина [math] v_{n} [/math] не может быть смежной ни с одной из [math] m [/math] вершин [math] v_{{i}_{j-1}} [/math] для [math] 1 \leqslant j \leqslant m [/math]. Но поскольку [math] v_{1} [/math] и [math] v_{n} [/math] не смежны, а [math] v_{n} [/math] имеет степень не меньше [math] n/2 [/math], то, как было показано в первой части доказательства, [math] m [/math] должно быть меньше чем [math] (n-1)/2 [/math]. Так как по предположению число вершин со степенями, не превосходящими [math] m [/math], меньше чем [math] m [/math], то хотя бы одна из [math] m [/math] вершин [math] v_{{i}_{j-1}} [/math], скажем [math] v' [/math], должна иметь степень не меньше [math] n/2 [/math]. Итак, мы установили, что степени двух несмежных вершин [math] v_{n} [/math] и [math] v' [/math] не меньше [math] n/2 [/math]. Полученное противоречие завершает доказательство теоремы.
[math]\triangleleft[/math]

Замечания

  • Приведенное достаточное условие не является необходимым.
  • Условия теоремы нельзя улучшить, так как при их ослаблении новое условие уже не будет достаточным для гамильтоновости графа.

Ограничивая условия теоремы Поша, получаем более простые, но менее сильные достаточные условия, найденные Оре и Дираком соответственно:

Теорема (Следствие 1):
Если [math] n \geqslant 3 [/math] и [math] \deg u + \deg v \geqslant n [/math] для любой пары [math] u [/math] и [math] v [/math] несмежных вершин графа [math] G [/math], то [math] G [/math] — гамильтонов граф.
Теорема (Следствие 2):
Если [math] n \gt 3 [/math] и [math] \deg v \geqslant n/2 [/math] для любой вершины [math] v [/math] графа [math] G [/math], то [math] G [/math] — гамильтонов граф.

Источники

  • Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 60 с.
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Обсуждение_участника:NikitaMarkovnikov&oldid=40194»